Đề kiểm tra Hệ trục tọa độ trong không gian (có lời giải) - Đề 1
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow a = 3\overrightarrow i + 4\overrightarrow j - \overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \)là
\(\overrightarrow a \left( {3\;;\;4\;;\;1} \right)\).
\(\overrightarrow a \left( {3\;;\;0\;;\;1} \right)\).
\(\overrightarrow a \left( {3\;;\;4\;;\; - 1} \right)\).
\(\overrightarrow a \left( {3\;;\;0\;;\;0} \right)\).
Trong không gian \(Oxyz\), cho đoạn thẳng \(AB\) có \(A\left( {3\;;\;1\;;\; - 1} \right)\)và \(B\left( { - 1\;;\;5\;;\;7} \right)\). Tọa độ trung điểm \(M\)của \(AB\)là
\(M\left( {2\;;\;6\;;\;6} \right)\).
\(M\left( {1\;;\;3\;;\;3} \right)\).
\(M\left( { - 1\;;\;3\;;\; - 3} \right)\).
\(\overrightarrow a \left( { - 2\;;\; - 6\;;\; - 6} \right)\).
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\). Biết \(A\left( {1;0;1} \right)\), \(C'\left( {4;5; - 5} \right)\). Tìm tọa độ tâm \(I\) của hình hộp.
\(I\left( {5;5; - 2} \right)\).
\(I\left( { - \frac{5}{2};\frac{5}{2}; - 2} \right)\).
\(I\left( {\frac{5}{2};\frac{5}{2};2} \right)\).
\(I\left( {\frac{5}{2};\frac{5}{2}; - 2} \right)\).
Trong không gian \(Oxyz\), cho \(\vec a = \left( {2; - 3;3} \right)\), \(\vec b = \left( {0;2; - 1} \right)\), \(\vec c = \left( {3; - 1;5} \right)\). Tìm tọa độ của vectơ \(\vec u = 2\vec a + 3\vec b - 2\vec c\).
\(\left( {10; - 2;13} \right)\).
\(\left( { - 2;2; - 7} \right)\).
\(\left( { - 2; - 2;7} \right)\).
\(\left( { - 2;2;7} \right)\).
Cho tứ giác\(ABCD\) biết \(A\left( {0;\, - 2;\,1} \right),\,\,B\left( {1;\,3;\, - 2} \right),\,\,C\left( {1;\,0;\,0} \right)\). Tìm tọa độ điểm \(D\) để tứ giác \(ABCD\) là hình bình hành.
\(D\left( {0;\, - 5;\,3} \right)\).
\(D\left( {0;\,5;\,3} \right)\).
\(D\left( {1;\,5;\, - 3} \right)\).
\(D\left( {0;\, - 5;\, - 3} \right)\).
Trong không gian \[Oxyz\] tìm tọa độ của điểm \[A\] biết điểm \[A\] nằm trên tia \[Oy\] và \[OA = 3\].
\(A\left( {0;\,\,3;\,0} \right)\).
\(A\left( {1;\,\, - 3;\,0} \right)\).
\(A\left( {3;\,0;\,0} \right)\).
\(A\left( {0;\,\,0;\,3} \right)\).
Trong không gian \[Oxyz\], cho điểm \[I\left( { - 5;0;5} \right)\] là trung điểm của đoạn \[MN\], biết \[M\left( {1; - 4;7} \right)\]. Tìmtọa độ của điểm \[N\].
\[N\left( { - 10;4;3} \right)\].
\[N\left( { - 11; - 4;3} \right)\].
\[N\left( { - 2; - 2;6} \right)\].
\[N\left( { - 11;4;3} \right)\].
Cho các vectơ \[\vec a = \left( {1;2;3} \right);\,\,\vec b = \left( { - 2;4;1} \right);\,\,\vec c = \left( { - 1;3;4} \right)\]. Vectơ \[\overrightarrow v = 2\overrightarrow a - 3\overrightarrow b + 5\overrightarrow c \] có tọa độ là
\[\left( {{\rm{3}};{\rm{7;23}}} \right)\].
\[\left( {{\rm{7}};{\rm{3}};{\rm{23}}} \right)\].
\[\left( {{\rm{23}};{\rm{7}};{\rm{3}}} \right)\].
\[\left( {{\rm{7}};{\rm{23}};{\rm{3}}} \right)\].
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A\prime B\prime C\prime D\prime \) có đỉnh \(A\prime \) trùng với gốc \(O\) và các đỉnh \(D\prime ,B\prime ,A\) lần lượt thuộc các tia \(Ox\), \(Oy\), \(Oz\) như hình vẽ. Giả sử đỉnh \(C\) có toạ độ là \((2;3;4)\) đối với hệ toạ độ \(Oxyz\). Khi đó toạ độ điểm \(B\) là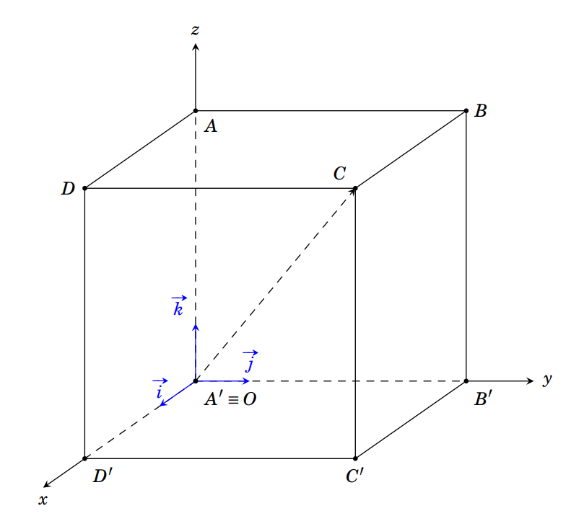
\(B\left( {3;0;4} \right)\).
\(B\left( {0;3;4} \right)\).
\(B\left( {2;4;0} \right)\).
\(B\left( {0;2;4} \right)\).
Cho hình hộp chữ nhật \(OABC.O\prime B\prime C\prime \) có cạnh \(OA = 4\), \(OC = 6\), \(OO\prime = 3\). Chọn hệ trục toạ độ \(Oxyz\) có gốc toạ độ \(O\); các điểm \(A,C,O\prime \) lần lượt nằm trên các tia \(Ox\), \(Oy\), \(Oz\). Khi đó toạ độ điểm \(B'\)là
\(B'(6;3;4)\).
\(B'(6;4;3)\).
\(B'(4;6;3)\).
\(B'(4;3;6)\).
Cho điểm \(M\left( {3; - 2;0} \right);N\left( {2;4;1} \right)\). Tọa độ của\(\overrightarrow {MN} \) là:
\(\left( {1; - 6; - 1} \right)\).
\(\left( { - 1;6;1} \right)\).
\(\left( {1;0;6} \right)\).
\(\left( { - 1;6; - 1} \right)\).
Một căn phòng có dạng hình hộp chữ nhật \(ABCD.A'B'C'D'\)với chiều rộng\(AB = 4\), chiều dài \(AD = 8\), chiều cao \(AA' = 10\) được gắn vào hệ trục \(Oxyz\) như hình vẽ. Người ta muốn treo một bóng đèn ở tâm hình hộp. Tìm tọa độ vị trí điểm \(M\) để treo bóng đèn.
\(M\left( {4;8;5} \right)\).
\(M\left( {2;4;10} \right)\).
\(M\left( {4;4;5} \right)\).
\(M\left( {2;4;5} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vec tơ \(\overrightarrow a \left( {1;\,\, - 2;\,\,0} \right)\) và \(\overrightarrow b \left( { - 2;\,\,3;\,\,1} \right)\). Xét tính đúng sai của các mệnh đề sau:
a) \(\overrightarrow a .\overrightarrow b = - 8\).
b) \(\left| {\overrightarrow b } \right| = 14\).
c) \(\overrightarrow a + \overrightarrow b = \left( { - 1;\,\,1;\,\, - 1} \right)\).
d) \(2\overrightarrow a = \left( {2;\,\, - 4;\,\,2} \right)\).
Trong hệ trục tọa độ \[Oxyz\], cho ba điểm \(A\left( {0;\, - 2;\,1} \right);\,B\left( { - 2;\, - 2;\, - 1} \right);\,C\left( {3;\,1;\, - 2} \right)\).Xét tính đúng sai của các mệnh đề sau:
a) Hình chiếu của \[A\] lên mặt phẳng \(\left( {Oxz} \right)\) là \(A'\left( {0;0;1} \right)\).
b) Tam giác \[ABC\] là tam giác vuông tại \(A\).
c) Tứ giác \[ABCD\] là hình bình hành thì tọa độ của \(D\left( {5;1;4} \right)\).
d) Trọng tâm của tam giác \[ABC\] là \(G\left( {\frac{1}{3};1;\frac{{ - 2}}{3}} \right)\).
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đỉnh \(A\) trùng với gốc tọa độ \(O\) và các đỉnh \(B\); \(C\); \(D'\) có tọa độ lần lượt là \(\left( {2\,;0\,;0} \right)\); \(\left( {2\,;4\,;0} \right)\); \(\left( {0\,;4\,;3} \right)\). Xét tính đúng sai của các khẳng định sau
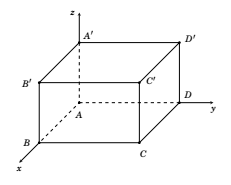
a) Tọa độ \(D\left( {0\,;4\,;0} \right)\).
b) Tọa độ \(C'\left( {2\,;3\,;4} \right)\).
c) Tọa độ của \(\overrightarrow {AA'} = \left( {0\,;0\,;3} \right)\).
d) Tọa độ của \(\overrightarrow {B'D} = \left( { - 2\,;4\,; - 3} \right)\).
Trong không gian \(Oxyz\), cho \(M\left( {8\,;4\,;3} \right)\). Xét tính đúng sai của các khẳng định sau
a) Hình chiếu vuông góc của \(M\) trên trục \(Ox\) là điểm \(\left( {0\,;4\,;3} \right)\).
b) Hình chiếu vuông góc của \(M\) trên trục \(Oz\) là điểm \(\left( {0\,;0\,;3} \right)\).
c) Hình chiếu vuông góc của \(M\) trên mặt phẳng \(Oxz\) là điểm \(\left( {8\,;0\,;3} \right)\).
d) \(\overrightarrow {OM} = 8\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k \).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 17 đến câu 22.
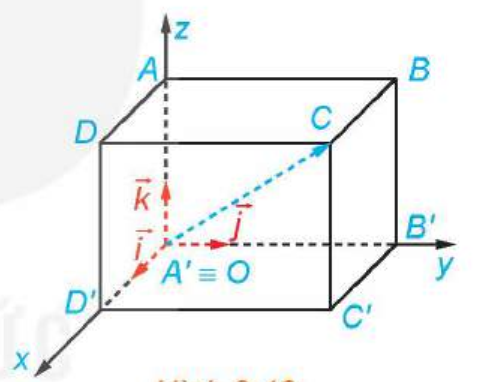
Trong không gian \(Oxyz\) cho hình hộp chữ nhật\(ABCD.A'B'C'D'\) có đỉnh \(A'\) trùng với gốc \(O\) và các đỉnh \(A',B',A\)lần lượt thuộc các tia \(Ox,Oy,Oz\). Giả sử đỉnh \(C'\) có tọa độ là \(\left( { - 3;4; - 6} \right)\) với hệ tọa độ\(Oxyz\), hãy tìm tọa độ các đỉnh \(D',B',A\)đối với hệ tọa độ \(Oxyz\)đó.
Trong không gian \(Oxyz\) cho lăng trụ tam giác\(ABC.A'B'C'\) có đỉnh \(A\left( {1; - 2;3} \right),B\left( { - 2;0;1} \right),A'\left( {3;2;2} \right)\) và \(C'\left( {4;3; - 2} \right).\)Tìm tọa độ các véc tơ \(\overrightarrow {AB} ,\overrightarrow {AA'} \) và tìm tọa độ các điểm \(C\)và \(B'.\)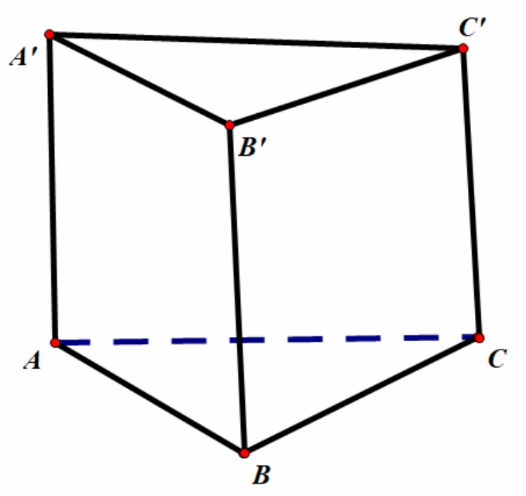
Trong không gian \(Oxyz\), cho hình lập phương \(ABCD.A'B'C'D'\) có \(A\left( {0;0;0} \right),B\left( {2;0;0} \right);D\left( {0;2;0} \right);A'\left( {0;0;2} \right)\). Tìm tọa độ điểm\(C'\)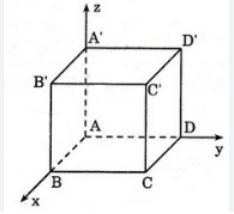
Gạch ống là một sản phẩm được tạo hình thành từ đất sét và nước, được kết hợp lại ới nhau theo một công thức chung hợp lý mới có thể tạo ra hỗ hợp dẻo quoánh, sau đó chúng được đổ vào khuôn, rồi đem phơi hoặc sất khô và cuối cùng là đưa vào lò nung. Một viên gạch hình hộp chữ nhật có kích thước dài \(20cm\),rộng \(8cm\). Bên trong có bốn lỗ hình trụ bằng nhau có đường kính \(2,5cm.\)

Tính thể tích đất sét để làm một viên gạch. (Lấy \(\pi = 3,14\)).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\Delta ABC\] biết \[A\left( {2;0;0} \right)\], \[B\left( {0;2;0} \right)\], \[C\left( {1;1;3} \right)\]. \[H\left( {{x_0};{y_0};{z_0}} \right)\] là chân đường cao hạ từ đỉnh \[A\] xuống \[BC\]. Khi đó \[{x_0} + {y_0} + {z_0}\] bằng bao nhiêu? (làm tròn đến hàng phần trăm).
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát \(2,5{\rm{\;km}}\) về phía nam và \({\rm{2\;km}}\) về phía đông, đồng thời cách mặt đất \(0,8{\rm{\;km}}\). Chiếc thứ hai nằm cách điểm xuất phát \(1,5{\rm{\;km}}\) về phía bắc và \(3{\rm{ km}}\) về phía tây, đồng thời cách mặt đất \(0,6{\rm{\;km}}\). Người ta cần tìm một vị trí trên mặt đất để tiếp nhiên liệu cho hai khinh khí cầu sao cho tổng khoảng cách từ vị trí đó tới hai khinh khí cầu nhỏ nhất. Giả sử vị trí cần tìm cách địa điểm hai khinh khí cầu bay lên là \(a\,{\rm{km}}\) theo hướng nam và \(b\,{\rm{km}}\) theo hướng tây. Tính tổng \(2a + 3b\).








