Đề kiểm tra Hệ trục tọa độ trong không gian (có lời giải) - Đề 3
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian với hệ tọa độ \(Oxyz\), cho các điểm \(A\left( {3; - 4;0} \right)\). Toạ độ \(\overrightarrow {OA} \) là
\(\left( {3;0;0} \right)\)
\(\left( {3; - 4;0} \right)\)
\(\left( {0; - 4;0} \right)\)
\(\left( {0;0;0} \right)\)
Trong không gian với hệ trục tọa độ \[Oxyz\], cho \[\vec a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \]. Tọa độ của vectơ \[\vec a\] là
\[\left( { - 1;2; - 3} \right)\].
\(\left( {2; - 3; - 1} \right)\).
\(\left( {2; - 1; - 3} \right)\).
\[\left( { - 3;2; - 1} \right)\].
Trong không gian \(Oxyz\), cho \[\vec a = \left( {0; - 3;2} \right)\]. Mệnh đề nào dưới đây đúng?
\[\overrightarrow a = - 3\overrightarrow i + 2\overrightarrow j \].
\[\overrightarrow a = - 3\overrightarrow i + 2\overrightarrow j + \overrightarrow k \].
\[\overrightarrow a = - 3\overrightarrow j + 2\overrightarrow k \].
\[\overrightarrow a = - 3\overrightarrow i + 2\overrightarrow k \].
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;\,1;\, - 2} \right)\) và \(B\left( {2;\,2;\,1} \right)\). Vectơ \(\overrightarrow {AB} \) có tọa độ là
\(\left( { - 1;\, - 1;\, - 3} \right)\)
\(\left( {3;\,1;\,1} \right)\)
\(\left( {1;\,1;\,3} \right)\)
\(\left( {3;\,3;\, - 1} \right)\)
Trong không gian với hệ toạ độ \(Oxyz\), cho hình lập phương \(ABCD.A'B'C'D'\) có đỉnh \(A\) trùng với gốc toạ độ \(O\), điểm \(B\left( {1;0;0} \right)\), \(D\left( {0;1;0} \right)\), \(D'\left( {0;1; - 1} \right)\). Tìm toạ độ vectơ \(\overrightarrow {CA'} \) tương ứng là
\(\left( { - 1;1;0} \right).\)
\(\left( {1; - 1; - 1} \right).\)
\(\left( { - 1; - 1; - 1} \right).\)
\(\left( {1;0; - 1} \right).\)
Trong không gian với hệ toạ độ \(Oxyz\), cho hình lập phương \(ABCD.A'B'C'D'\) có đỉnh \(A\) trùng với gốc toạ độ \(O\), điểm \(B\left( {1;0;0} \right)\), \(D\left( {0;1;0} \right)\), \(D'\left( {0;1; - 1} \right)\). Tìm toạ độ vectơ\(\overrightarrow {B'D'} \) tương ứng là
\(\left( { - 1;1;0} \right).\)
\(\left( {1; - 1; - 1} \right).\)
\(\left( { - 1; - 1; - 1} \right).\)
\(\left( {1;0; - 1} \right).\)
Trong không gian \({\rm{O}}xyz\), gọi \(A'\) là hình chiếu vuông góc của điểm \(A\left( {1;2;3} \right)\) trên mặt phẳng\(\left( {Oyz} \right)\) thì vectơ \[\overrightarrow {AA'} \] là
\(\left( {0;\,2;\,3} \right)\).
\(\left( { - 1;\,0;\,0} \right)\).
\(\left( {1;\,0;\,0} \right)\).
\(\left( {0;\,2;\,0} \right)\).
Trong không gian \[Oxyz\], gọi \(M'\) là hình chiếu vuông góc của điểm \(M\left( {2;3; - 1} \right)\)trên trục \[Oy\]thì vectơ\[\overrightarrow {MM'} \] là
\(\left( {0;\,2;\,3} \right)\).
\(\left( { - 2;0;1} \right).\)
\(\left( {3;0;0} \right).\)
\(\left( {0;3;0} \right).\)
Trong không gian \(Oxyz\), vectơ đơn vị trên trục \(Oy\) là
\(\overrightarrow j = \left( {0;1;0} \right)\).
\(\overrightarrow i = \left( {1;0;0} \right)\).
\(\overrightarrow k = \left( {0;0;1} \right)\).
\(\overrightarrow n = \left( {1;1;1} \right)\).
Trong không gian \(Oxyz\), cho điểm \(A = \left( {4; - 2;3} \right)\). Tìm vectơ \(\overrightarrow {AO} \).
\(\left( { - 4;2; - 3} \right)\).
\(\left( { - 2;3;4} \right)\).
\(\left( { - 2;4;3} \right)\).
\(\left( {4;2; - 3} \right)\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1\;;\; - 2\;;\;7} \right)\). Gọi \({A_1},\;{A_2},\;{A_3}\) lần lượt là hình chiếu vuông góc của điểm \(A\) trên các trục \(Ox,\;Oy,\;Oz\). Tìm tọa độ các điểm \({A_1},\;{A_2},\;{A_3}\)?
Trong không gian \(Oxyz\), cho điểm \(A\left( {1\;;\; - 2\;;\;7} \right)\). Gọi \({A_1},\;{A_2},\;{A_3}\) là hình chiếu vuông góc của điểm \(A\) trên các mặt phẳng tọa độ \[\left( {Oxy} \right);\;\left( {Oxz} \right);\;\left( {Oyz} \right)\]. Tìm tọa độ các điểm \({A_1},\;{A_2},\;{A_3}\)?
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1\;;\; - 2\;;\;7} \right);\;B\left( {5\;;6\;;\;3} \right);\;C\left( { - 4\;;\;7\;;\;10} \right)\).
a) Tìm tọa độ các vectơ \(\overrightarrow {AB} ;\;\overrightarrow {AC} ;\;\overrightarrow {BC} \)?
b) Chứng minh rằng ba điểm \(A,\;B,\;C\) không thẳng hàng?
c) Tính chu vi của tam giác \(ABC\)?
d) Tính diện tích tam giác \(ABC\)?
Trong không gian \(Oxyz\), cho ba vectơ \(\overrightarrow {OA} = \left( {1\;;\; - 2\;;\;7} \right)\); \(\overrightarrow {OB} = \left( {5\;;6\;;\;3} \right)\); \(\overrightarrow {AC} = \left( { - 4\;;\;7\;;\;10} \right);\;\)\(\overrightarrow {BD} = \left( { - 10\;;0\;;\;8} \right)\). Tìm tọa độ các điểm \(A,\;B,\;C,\;D\)?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1\;;\; - 2\;;\;7} \right);\;B\left( {5\;;6\;;\;3} \right);\;C\left( { - 4\;;\;7\;;\;10} \right)\).
a) Tìm tọa độ trung điểm \(I\) của đoạn \(AB\)?
b) Tìm tọa độ trung điểm \(J\) của đoạn \(AC\)?
c) Tìm tọa độ trung điểm \(K\) của đoạn \(BC\)?
d) Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\)?
e) Tìm tọa độ trọng tâm \(Q\) của tam giác \(OAB\)?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1\;;\; - 2\;;\;7} \right);\;B\left( {5\;;6\;;\;3} \right);\;C\left( { - 4\;;\;7\;;\;10} \right);\;G\left( {2\;;\;5\;;\;6} \right)\).
a) Tìm tọa độ điểm \(M\) đối xứng với điểm \(A\) qua \(B\) ?
b) Tìm tọa độ điểm \(N\) đối xứng với điểm \(B\) qua \(C\)?
c) Tìm tọa độ điểm \(B'\) đối xứng với điểm \(B\) qua trục \(Oy\)?
d) Tìm tọa độ điểm \(C'\) đối xứng với điểm \(C\) qua mặt phẳng tọa độ \(\left( {Oxz} \right)\) ?
e) Tìm tọa độ điểm \(D\) sao cho \(G\) là trọng tâm của tam giác \(BCD\)?
f) Tìm tọa độ điểm \(K\) sao cho \(A\) là trọng tâm của tam giác \(KBG\)?
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Trong không gian \(Oxyz\), cho điểm \(K\left( {5\;; - 6\;;\;3} \right);\;H\left( { - 4\;;\;7\;;\; - 10} \right)\) và \(\overrightarrow u = \left( {6\;;\; - 5\;;\; - 9} \right)\).
a) Tìm tọa độ điểm \(D\) sao cho \(\overrightarrow {DK} = \overrightarrow u \) ?
b) Tìm tọa độ điểm \(M\) sao cho \(\overrightarrow {HM} = 2\overrightarrow u \)?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1\;;\; - 2\;;\;7} \right);\;B\left( {5\;;6\;;\;3} \right);\;C\left( { - 4\;;\;7\;;\;10} \right)\).
a) Tìm tọa độ điểm \(D\) sao cho tứ giác \(ABCD\) là hình bình hành?
b) Tìm tọa độ điểm \(M\) sao cho tứ giác \(ABMC\) là hình bình hành?
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) với các đỉnh \[A( - 1\;;\;1\;;\;2);\]\[B( - 3\;;\;2\;;\;1)\]; \[D(0\;;\; - 1;\;2)\] và \[A'(2\;;\;1\;;\;2)\]. Tìm tọa độ các đỉnh của hình hộp?
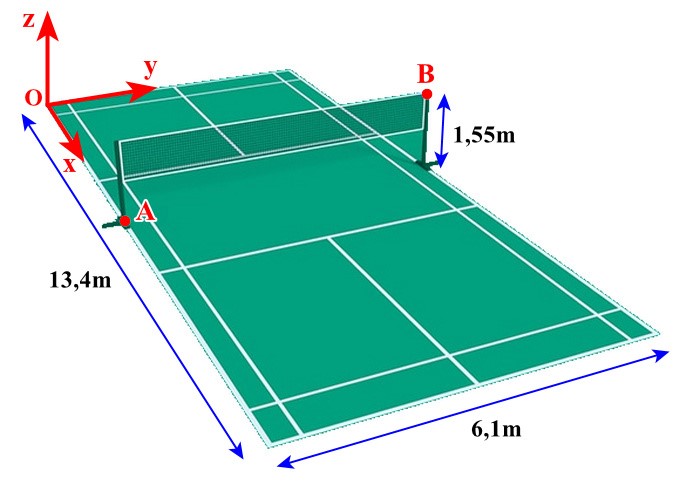
Hình dưới đây mô tả một sân cầu lông với kích thức theo tiêu chuẩn quốc tế. Ta chọn hệ trục \(Oxyz\)cho sân đó (đơn vị trên mỗi trục là mét) và hai điểm\(A,\,B\)như hình. Xác định tọa độ của \(\overrightarrow {AB} \).
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát \(2\;km\) về phía nam và \(1\;km\) về phía đông, đồng thời cách mặt đất \(0,5\;m\). Chiếc thứ hai nằm cách điểm xuất phát \(1\;km\) về phía bắc và \(1,5\;km\) về phía tây, đồng thời cách mặt đất \(0,8\;km\). Chọn hệ trục tọa độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất với trục \(Ox\) hướng về phía nam, \(Oy\) hướng về phía đông, \(Oz\) hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét. Tìm tọa độ của mỗi chiếc khinh khí cầu.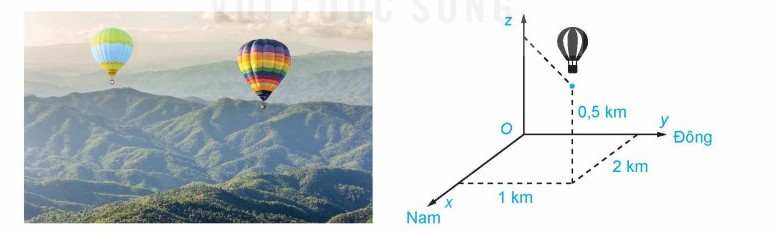
Trong không gian với một hệ trục tọa độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm \(A\left( {800\;;\;500\;;\;7} \right)\) đến điểm \(B\left( {940\;;\;550\;;\;8} \right)\) trong vòng \(10\) phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau \(10\) phút tiếp theo là gì?









