30 câu hỏi
Cho $a > 0,m,n \in \mathbb{R}$. Khẳng định nào sau đây đúng?
${a^m} + {a^n} = {a^{m + n}}.$
${a^m} \cdot {a^n} = {a^{m - n}}.$
${\left( {{a^m}} \right)^n} = {\left( {{a^n}} \right)^m}.$
$\frac{{{a^m}}}{{{a^n}}} = {a^{n - m}}$.
Cho $a$ là số thực dương khác $1$. Khi đó $\sqrt[8]{{{a^3}}}$ bằng
$\sqrt[3]{{{a^2}}}$.
${a^{\frac{8}{3}}}$.
${a^{\frac{3}{8}}}$.
$\sqrt[6]{a}$.
Nếu $m$ là số nguyên dương, biểu thức nào sau đây không bằng với ${\left( {{2^4}} \right)^m}$?
${4^{2m}}$.
${2^m} \cdot \left( {{2^{3m}}} \right)$.
${4^m} \cdot \left( {{2^m}} \right)$.
${2^{4m}}$.
Cho ${4^x} + {4^{ - x}} = 7$. Khi đó biểu thức $P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + 4 \cdot {2^x} + 4 \cdot {2^{ - x}}}} = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản và $a,b \in \mathbb{Z}$. Tích $ab$ có giá trị bằng
$10$.
$ - 8$.
$8$.
$ - 10$.
Cho hai số dương $a,\,\,b\,\,\left( {a \ne 1} \right)$. Mệnh đề nào dưới đây sai?
${\log _a}a = 2a$.
\[{\log _a}{a^\alpha } = \alpha \].
${\log _a}1 = 0$.
${a^{{{\log }_a}b}} = b$.
Với $a,b$ là các số thực dương tùy ý và $a \ne 1$, ${\log _{{a^5}}}b$ bằng
$5{\log _a}b$.
$\frac{1}{5} + {\log _a}b$.
$5 + {\log _a}b$.
$\frac{1}{5}{\log _a}b$.
Cho $a$ là số thực dương khác $1.$ Giá trị của ${a^{{{\log }_{\sqrt a }}4}}$ là
8.
$4$.
$2$.
16.
Cho ${\log _2}x = \sqrt 2 $. Giá trị của biểu thức $A = {\log _2}{x^2} + {\log _{\frac{1}{2}}}{x^3} + {\log _4}x$ bằng
$\frac{{\sqrt 2 }}{2}$.
$ - \frac{{\sqrt 2 }}{2}$.
$\sqrt 2 $.
$ - \sqrt 2 $.
A. $y = {2^x}$.
$y = {\log _3}x$.
$y = {\log _3}x$.
$y = \ln x$.
$y = {x^{ - 5}}$.
Tập xác định của hàm số $y = {\log _3}x$ là
$\left[ {3\,;\, + \infty } \right)$.
$\left( { - \infty \,;\, + \infty } \right)$.
$\left[ {0\,;\, + \infty } \right)$.
$\left( {0\,;\, + \infty } \right)$.
Hàm số nào dưới đây có đồ thị như hình dưới?
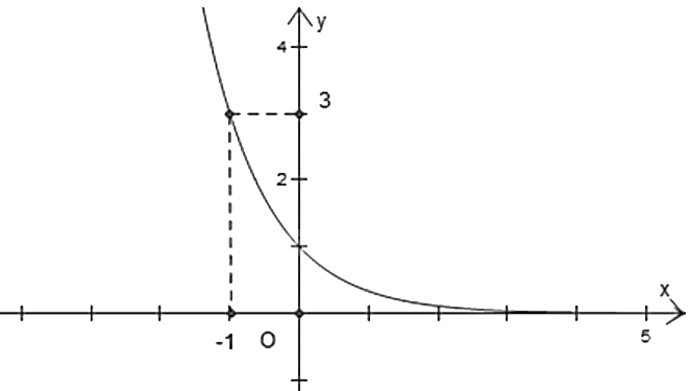
$y = {3^x}$.
$y = {\left( {\frac{1}{2}} \right)^x}$.
$y = {\left( {\frac{1}{3}} \right)^x}$.
$y = {\left( {\sqrt 2 } \right)^x}$.
Hàm số $y = {\log _2}x$ đồng biến trên khoảng nào sau đây?
$\left( { - 1;\, + \infty } \right)$.
$\left[ {0;\, + \infty } \right)$.
$\left[ { - 1;\,\, + \infty } \right)$.
$\left( {1;\, + \infty } \right)$.
Nghiệm của phương trình ${3^x} = 7$ là
$x = {\log _7}3$.
$x = {\log _3}7$.
$x = {3^{ - 7}}$.
$x = \frac{7}{3}$.
Tập nghiệm của bất phương trình ${\log _{\frac{1}{2}}}x \leqslant - 3$ là
$S = \left( { - \infty ;8} \right]$.
$S = \left[ {8; + \infty } \right)$.
$S = \left( {0;8} \right]$.
$S = \left[ { - 8; + \infty } \right)$.
Số nghiệm nguyên của bất phương trình ${\log _{\frac{1}{2}}}\left( {4x - 9} \right) > {\log _{\frac{1}{2}}}\left( {x + 10} \right)$ là
\[6\].
Vô số.
\[0\].
\[4\].
Chọn đáp án đúng.
Nếu hàm số $y = f\left( x \right)$ có đạo hàm tại ${x_0}$ thì phương trình tiếp tuyến của đồ thị hàm số đó tại điểm $M\left( {{x_0};\,f\left( {{x_0}} \right)} \right)$ là
\[y = f'\left( x \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\].
\[y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\].
\[y = f'\left( x \right)\left( {x - {x_0}} \right) - f\left( {{x_0}} \right)\].
\[y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) - f\left( {{x_0}} \right)\].
Cho hàm số $y = f\left( x \right)$ có $\mathop {\lim }\limits_{x \to - 2} \frac{{f\left( x \right) - f\left( { - 2} \right)}}{{x + 2}} = 5$. Khi đó, $f'\left( 2 \right)$ bằng
\[5\].
\[ - 5\].
\[2\].
\[ - 2\].
Cho hàm số $f\left( x \right) = {x^3} + 2{x^2} + 1$ có đồ thị là $\left( C \right)$. Tiếp tuyến với $\left( C \right)$tại điểm có hoành độ $x = 1$ có phương trình là
$y = 7x + 2$.
$y = - x + 5$.
$y = 7x - 3$.
$y = 3x + 1$.
Chọn khẳng định đúng?
${\left( {\ln x} \right)^\prime } = \frac{1}{x}\,\,\left( {x > 0} \right)$.
${\left( {\ln x} \right)^\prime } = x\,\,\left( {x > 0} \right)$.
${\left( {\ln x} \right)^\prime } = \frac{e}{x}\,\,\left( {x > 0} \right)$.
${\left( {\ln x} \right)^\prime } = e \cdot x\,\,\left( {x > 0} \right)$.
Cho hai hàm số $u\left( x \right)$ và $v\left( x \right)$ có đạo hàm tại điểm $x$ thuộc tập xác định. Khẳng định nào dưới đây là đúng?
${\left( {uv} \right)^\prime } = u' \cdot v'$.
${\left( {uv} \right)^\prime } = u'v$.
${\left( {uv} \right)^\prime } = u'v + uv'$.
${\left( {uv} \right)^\prime } = uv'$.
Đạo hàm của hàm số $y = \cos x$ tại $x = \frac{\pi }{3}$ là
$ - \frac{{\sqrt 3 }}{2}$.
$\frac{{\sqrt 3 }}{2}$.
$\frac{1}{2}$.
$ - \frac{1}{2}$.
Đạo hàm cấp hai của hàm số $y = {x^7}$ là
\[y'' = 7{x^6}\].
$y'' = 42{x^5}$.
$y'' = 13{x^5}$.
$y'' = 7{x^5}$.
Hai đường thẳng $a$ và $b$ được gọi là vuông góc với nhau nếu
chúng cắt nhau.
góc giữa chúng bằng $90^\circ $.
góc giữa chúng bằng $180^\circ $.
góc giữa chúng bằng $0^\circ $.
Góc giữa hai đường thẳng không thể bằng
\[30^\circ \].
$56^\circ $.
$90^\circ $.
$170^\circ $.
Cho hình hộp chữ nhật \[ABCD.EFGH\]. Xác định số đo góc giữa hai đường thẳng $AE$ và $CD$.
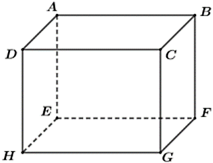
$90^\circ .$
$30^\circ .$
$60^\circ .$
$45^\circ .$
Cho tứ diện $ABCD$. Lấy điểm $I$ bất kì thuộc cạnh $AC$. Qua $I$ kẻ đường thẳng song song với $AB$ cắt $BC$ tại $M$. Qua $I$ kẻ đường thẳng song song với $CD$ cắt $AD$ tại $N$. Khi đó, góc giữa hai đường thẳng $AB$ và $CD$ bằng góc giữa hai đường thẳng
$IM,\,\,MN.$
$IN,\,\,NM.$
$IM,\,\,IN.$
$IM,\,\,IC.$
Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$. Chọn đáp án đúng nhất.
$SA \bot AB.$
$SA \bot AC.$
$SA \bot BC.$
Cả ba đáp án A, B, C đều đúng.
Cho đường thẳng $a$ vuông góc với mặt phẳng $\left( P \right)$, đường thẳng $b$ vuông góc với đường thẳng $a$. Phát biểu nào sau đây là đúng?
Đường thẳng $b$ cắt mặt phẳng $\left( P \right)$.
Đường thẳng $b$ song song mặt phẳng $\left( P \right)$.
Đường thẳng $b$ nằm trên mặt phẳng $\left( P \right)$.
Đường thẳng $b$ nằm trên mặt phẳng $\left( P \right)$ hoặc song song với mặt phẳng $\left( P \right)$.
Cho hình chóp \[S.ABC\] có \[SA \bot \left( {ABC} \right)\] (như hình vẽ dưới).
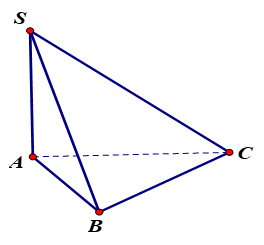
Hình chiếu của \[SC\] lên mặt phẳng \[\left( {ABC} \right)\] là
\[BC\].
\[AC\].
\[SB\].
\[AB\].
Một chiếc cột dựng trên nền sân phẳng. Gọi $O$ là điểm đặt chân cột trên mặt sân và $M$ là điểm trên cột cách chân cột 30 cm. Trên mặt sân, người ta lấy hai điểm $A$ và $B$ cách đều $O$ là 40 cm ($A,\,B,\,O$ không thẳng hàng). Người ta đo độ dài $MA$ và $MB$ đều bằng 50 cm. Chọn khẳng định đúng.
Tam giác $MOB$ là tam giác tù.
Tam giác $MOA$ là tam giác tù.
\[MO \bot \left( {AOB} \right)\].
Cả A, B, C đều đúng.
