12 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Với \(a\) là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
\({a^{\frac{5}{2}}}\).
\(a\).
\({a^{\frac{3}{2}}}\).
\({a^{\frac{1}{4}}}\).
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
\(\frac{5}{{2a}}\).
\(\frac{{5a}}{2}\).
\(\frac{2}{{5a}}\).
\(\frac{{2a}}{5}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{e}} \right)^x}\).
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\).
Tập nghiệm \(S\) của bất phương trình \(\log x < 1\) là
\(S = \left( { - \infty ;10} \right)\).
\(S = \left( {0;10} \right)\).
\(S = \left( {10; + \infty } \right)\).
\(S = \left( { - \infty ;1} \right)\).
Cho \({\log _a}b = 2\) với \(a,b\) là số thực dương và \(a\) khác 1. Tính giá trị biểu thức \(T = {\log _{{a^2}}}{b^6} + {\log _a}\sqrt b \).
\(T = 7\).
\(T = 6\).
\(T = 5\).
\(T = 8\).
Trong hình vẽ bên có đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\). Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
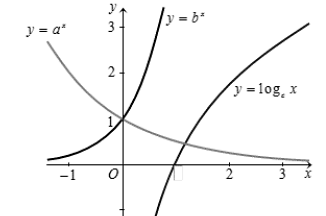
\(a < c < b\).
\(c < a < b\).
\(a < b = c\).
\(b < c < a\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Góc giữa hai đường thẳng \(SD\) và \(BC\) bằng
Góc giữa hai đường thẳng \(SD\) và \(DC\).
Góc giữa hai đường thẳng \(SD\) và \(AD\).
Góc giữa hai đường thẳng \(SD\) và \(BD\).
Góc giữa hai đường thẳng \(SD\) và \(SC\).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình vuông tâm \(O\). Hình chiếu của điểm \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là điểm
\(B\).
\(D\).
\(O\).
\(A\).
Cho hình chóp\(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Khẳng định nào dưới đây sai?
\(SA \bot AB\).
\(SA \bot BC\).
\(SA \bot AC\).
\(SB \bot AB\).
Cho các đường thẳng \(a,b\) và các mặt phẳng \(\left( \alpha \right),\left( \beta \right)\). Chọn mệnh đề đúng trong các mệnh đề sau
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\a \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot b\\a \bot \left( \alpha \right)\end{array} \right. \Rightarrow b//\left( \alpha \right)\).
\(\left\{ \begin{array}{l}a \bot b\\a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
\(\left\{ \begin{array}{l}\left( \alpha \right) \bot \left( \beta \right)\\a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow a \bot b\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\) và các cạnh bên bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm \(AD\) và \(SD\). Số đo góc \(\left( {MN,SC} \right)\) bằng
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
Cho tam giác \(ABC\) vuông cân tại \(B\) và \(AB = a\). Trên đường thẳng qua \(A\) vuông góc với \(\left( {ABC} \right)\) lấy điểm \(S\) sao cho \(SA = a\). Tính số đo góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\).
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
