35 câu hỏi
Cho $a$ là số thực dương. Với $n$ thuộc tập hợp nào thì khẳng định ${a^n} = \underbrace {a.a............a}_n$ đúng?
$n \in \mathbb{R}$.
$n \in \mathbb{Z}$.
$n \in \mathbb{N}$.
$n \in {\mathbb{N}^*}$.
Với $a$ là số thực dương tùy ý, $\sqrt {{a^3}} $ bằng kết quả nào sau đây?
${a^6}$.
${a^{\frac{3}{2}}}$.
${a^{\frac{2}{3}}}$.
${a^{\frac{1}{6}}}$.
Với $\alpha $ là số thực bất kì, mệnh đề nào sau đây sai?
\[\sqrt {{{10}^\alpha }} = {\left( {\sqrt {10} } \right)^\alpha }\].
\[\sqrt {{{10}^\alpha }} = {10^{\frac{\alpha }{2}}}\].
\[{\left( {{{10}^\alpha }} \right)^2} = {\left( {100} \right)^\alpha }\].
\[{\left( {{{10}^\alpha }} \right)^2} = {\left( {10} \right)^{{\alpha ^2}}}\].
Cho đẳng thức $\frac{{\sqrt[3]{{{a^2}\sqrt a }}}}{{{a^3}}} = {a^\alpha },0 < a \ne 1.$ Khi đó \[\alpha \] thuộc khoảng nào sau đây?
$\left( { - 2; - 1} \right)$.
$\left( { - 1;0} \right)$.
$\left( { - 3; - 2} \right)$.
$\left( {0;1} \right)$.
Chị Hà gửi vào ngân hàng $20\,\,000\,\,000$đồng với lãi suất \[0,5\% \]/tháng (sau mỗi tháng tiền lãi được nhập vào tiền gốc để tính lãi tháng sau). Hỏi sau \[1\] năm chị Hà nhận được bao nhiêu tiền, biết trong \[1\]năm đó chị Hà không rút tiền lần nào và lãi suất không thay đổi (làm tròn đến hàng nghìn).
$21\,\,233\,\,000$đồng.
$21\,\,235\,\,000$đồng.
$21\,\,234\,\,000$đồng.
$21\,\,200\,\,000$đồng.
Với điều kiện nào của $a,\,b$ thì khẳng định ${\log _a}b = \alpha \Leftrightarrow {a^\alpha } = b$ là đúng?
$a,\,\,b > 0,\,\,\,a \ne 1$.
$a,\,\,b > 0$.
$a > 0,\,a \ne 1$.
$\,b > 0,\,\,\,a \ne 1$.
Trong các mệnh đề sau, mệnh đề nào đúng?
\[{\log _a}{b^\alpha } = \alpha {\log _a}b\] với mọi số thực dương \[a,b\] và \[a \ne 1\].
\[{\log _a}{b^\alpha } = \alpha {\log _a}b\] với mọi số thực dương \[a,b\].
\[{\log _a}{b^\alpha } = \alpha {\log _a}b\] với mọi số thực\[a,b\].
\[{\log _a}{b^\alpha } = \alpha {\log _a}b\] với mọi số thực \[a,b\] và \[a \ne 1\].
Với $a$ là số thực dương tùy ý, ${\log _3}\left( {9a} \right)$ bằng
$\frac{1}{2} + {\log _3}a$.
$2{\log _3}a$.
${\left( {{{\log }_3}a} \right)^2}$.
$2 + {\log _3}a$.
Cho $0 < a \ne 1$. Giá trị của biểu thức $P = {\log _a}\left( {a \cdot \sqrt[3]{{{a^2}}}} \right)$là
$\frac{4}{3}$.
$3$.
$\frac{5}{3}$.
$\frac{5}{2}$.
Cho \[a,{\text{ }}b,{\text{ }}c\] là các số thực dương thỏa mãn \[{a^2} = bc.\]Giá trị của biểu thức \[S = 2\ln a - \ln b - \ln c\] là
\[S = 2\ln \left( {\frac{a}{{bc}}} \right).\]
$S = 1.$
\[S = - 2\ln \left( {\frac{a}{{bc}}} \right).\]
$S = 0.$
Hàm số nào dưới đây là hàm số mũ?
$y = {x^{\sqrt 3 }}$.
$y = {x^{\log 2}}$.
$y = {\log _{\sqrt 2 }}x$.
$y = {\left( {\frac{\pi }{3}} \right)^x}$.
Cho các hàm số sau:
$y = {\log _2}x$, $y = {\log _{\sqrt 3 }}x$, $y = \ln x$, $y = {\log _{{2^{ - 3}}}}x$, $y = {\log _x}5$.
Có bao nhiêu hàm số lôgarit trong các hàm số trên?
$5.$
$4.$
$3.$
$2.$
Tập xác định của hàm số \[y = {\log _2}x\] là
$\left[ {0; + \infty } \right).$
$\left( { - \infty ; + \infty } \right).$
$\left( {0; + \infty } \right).$
$\left[ {2; + \infty } \right).$
Cho ba số thực dương $a,b,c$ khác $1$. Đồ thị các hàm số $y = {a^x},y = {b^x},y = {c^x}$ được cho trong hình vẽ sau.
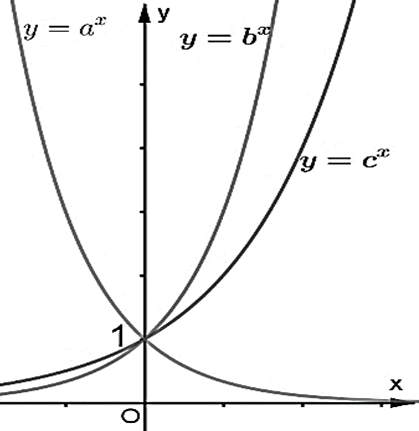
Mệnh đề nào dưới đây đúng?
$b < c < a$.
$c < a < b$.
$a < b < c$.
$a < c < b$.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
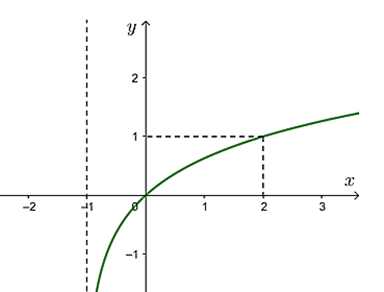
$y = {\log _2}x$.
\[y = {\log _2}\left( {x + 1} \right)\].
$y = {\log _3}x + 1$.
$y = {\log _3}\left( {x + 1} \right)$.
Nghiệm của phương trình ${7^x} = 2$ là
$x = {\log _7}2$.
$x = {\log _2}7$.
$x = \frac{2}{7}$.
$x = \sqrt 7 $.
Nghiệm của phương trình ${\log _3}\left( {5x} \right) = 2$ là
$x = \frac{8}{5}$.
$x = 9$.
$x = \frac{9}{5}$.
$x = 8$.
Tập nghiệm của bất phương trình ${\log _{\frac{2}{3}}}\left( {x - 2} \right) \geqslant 1$ là
$\left[ {\frac{8}{3}; + \infty } \right)$.
$\left[ {2;\frac{8}{3}} \right]$.
$\left( {2;\frac{8}{3}} \right]$.
$\left( { - \infty ;\frac{8}{3}} \right]$.
Tập nghiệm của bất phương trình \[{2^{x\, - \,3}}\, > \,16\] là
\[\left[ {7;\, + \infty } \right)\].
\[\left( {0;\, + \infty } \right)\].
\[\left( {7;\, + \infty } \right)\].
\[\left( {3;\, + \infty } \right)\].
Biết phương trình${4^x} - 9 \cdot {2^x} + 16 = 0$ có hai nghiệm phân biệt ${x_1},{x_2}$. Tính giá trị của biểu thức$A = {x_1} + {x_2}.$
$A = 4.$
$A = {\log _2}9.$
$A = 9.$
$A = 16.$
Trong không gian cho hai đường thẳng thẳng $m$ và $n$. Phát biểu nào sau đây là đúng?
Góc giữa hai đường thẳng $m$ và $n$ là góc giữa hai đường thẳng $a$ và $b$ cùng đi qua một điểm và tương ứng song song với $m$ và $n$.
Góc giữa hai đường thẳng $m$ và $n$ là góc giữa hai đường thẳng $m$ và $b$ vuông góc với $n$.
Góc giữa hai đường thẳng $m$ và $n$ là góc giữa hai đường thẳng $a$ và $b$ tương ứng vuông góc với $m$ và $n$.
Góc giữa hai đường thẳng $m$ và $n$ là góc giữa hai đường thẳng $a$ và $b$ bất kỳ.
Trong không gian, cho hai đường thẳng $a$ và $b$. Khẳng định nào sau đây là đúng?
Đường thẳng $a$ và $b$ vuông góc với nhau khi và chỉ khi chúng cắt nhau.
Đường thẳng $a$ và $b$ vuông góc với nhau khi và chỉ khi góc giữa chúng bằng $90^\circ $.
Đường thẳng $a$ và $b$ vuông góc với nhau khi và chỉ khi góc giữa chúng bằng $45^\circ $.
Đường thẳng $a$ và $b$ vuông góc với nhau khi và chỉ khi góc giữa chúng bằng $0^\circ $.
Cho hình lập phương $ABCD.A'B'C'D'$ (như hình vẽ dưới).
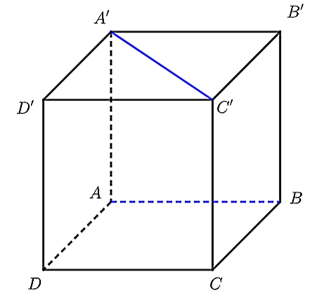
Góc giữa hai đường thẳng $AB$ và $A'C'$bằng
$60^\circ $.
$45^\circ $.
$90^\circ $.
$30^\circ $.
Cho hình lập phương $ABCD.A'B'C'D'$ (như hình vẽ dưới).
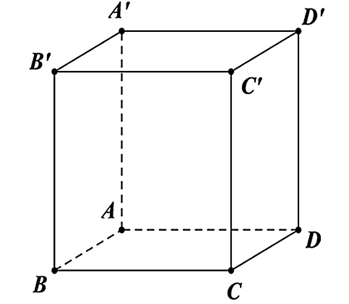
Đường thẳng nào sau đây vuông góc với đường thẳng $BC'$?
\[A'D\].
$AC$.
$BB'$.
$AD'$.
Trong không gian cho đường thẳng $d$ vuông góc với mọi đường thẳng $a$ nằm trong mặt phẳng $\left( \alpha \right)$. Khẳng định nào sau đây đúng?
$d{\text{//}}\left( \alpha \right)$ .
$d \bot \left( \alpha \right)$.
$d \subset \left( \alpha \right)$.
$d$ cắt $a$.
Cho tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc với nhau (tham khảo hình vẽ).
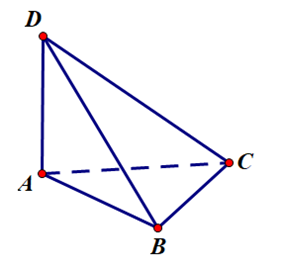
Khẳng định nào sau đây là đúng?
$AB \bot \left( {BCD} \right)$.
$AC \bot \left( {BCD} \right)$.
$AD \bot \left( {BCD} \right)$.
$AD \bot \left( {ABC} \right)$.
Cho hai đường thẳng $a,b$ và $mp\left( P \right)$. Chỉ ra mệnh đề đúng trong các mệnh đề sau:
Nếu $a{\text{//}}\left( P \right)$ và $b \bot a$ thì $b{\text{//}}\left( P \right)$.
Nếu $a{\text{//}}\left( P \right)$ và $b \bot \left( P \right)$ thì $a \bot b$.
Nếu $a{\text{//}}\left( P \right)$ và $b \bot a$ thì $b \bot \left( P \right)$.
Nếu $a \bot \left( P \right)$ và $b \bot a$ thì $b{\text{//}}\left( P \right)$.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật, $SA \bot \left( {ABCD} \right)$. Gọi $M,N$ lần lượt là trung điểm của $AB$ và $SB$(tham khảo hình vẽ).
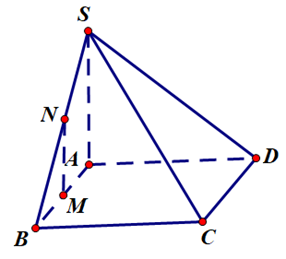
Khẳng định nào sau đây là đúng?
$AC \bot \left( {SAD} \right)$.
$MN \bot \left( {SBD} \right)$.
$BD \bot (SCD)$.
$MN \bot \left( {ABCD} \right)$.
Cho hình chóp $S.ABCD$ có đáy là hình vuông, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $H$ là hình chiếu vuông góc của $A$ lên mặt phẳng $\left( {SBC} \right)$.
Khẳng định nào sau đây là khẳng định đúng?
$H$ là chân đường vuông góc hạ từ $A$ lên \[SB\].
$H$ là trọng tâm tam giác \[SBC\].
$H$ trùng với \[B\].
$H$ là trung điểm của \[SB\].
Cho hai mặt phẳng $\left( \alpha \right)$, $\left( \beta \right)$. Phát biểu nào sau đây đúng?
Nếu $\left( \alpha \right)$ cắt $\left( \beta \right)$ thì $\left( \alpha \right) \bot \left( \beta \right)$.
Nếu $\left( {\left( \alpha \right),\left( \beta \right)} \right) = 0^\circ $ thì $\left( \alpha \right) \bot \left( \beta \right)$.
Nếu $\left( {\left( \alpha \right),\left( \beta \right)} \right) = 45^\circ $ thì $\left( \alpha \right) \bot \left( \beta \right)$.
Nếu $\left( {\left( \alpha \right),\left( \beta \right)} \right) = 90^\circ $thì $\left( \alpha \right) \bot \left( \beta \right)$.
Số cạnh bên của hình chóp cụt tứ giác đều là
$3$.
$4$.
$6$.
$12$.
Cho đường thẳng \[a\] vuông góc với mặt phẳng \[\left( \alpha \right)\] và \[a \subset \left( \beta \right)\]. Khẳng định nào sau đây là đúng?
$\left( \alpha \right)\,{\text{//}}\,\left( \beta \right)$.
$\left( \alpha \right)$trùng $\left( \beta \right)$.
$0^\circ \leqslant \left( {\left( \alpha \right),\left( \beta \right)} \right) < 90^\circ $.
$\left( \alpha \right) \bot \left( \beta \right)$.
Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, $SA$ vuông góc với đáy (tham khảo hình vẽ).
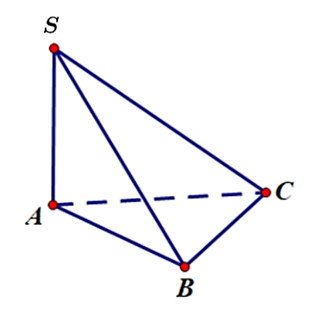
Khẳng định nào sau đây sai?
$\left( {SAB} \right) \bot \left( {ABC} \right)$.
$\left( {SAB} \right) \bot \left( {SAC} \right)$.
$\left( {SAC} \right) \bot \left( {ABC} \right)$.
$\left( {SAB} \right) \bot \left( {SBC} \right)$.
Cho tam giác $ABC$ cân tại $A$ có đường cao $AH = a\sqrt 3 ,\,BC = 3a$, $BC$ chứa trong mặt phẳng $\left( P \right)$. Gọi $A'$ là hình chiếu vuông góc của $A$ lên mặt phẳng $\left( P \right)$ (như hình vẽ bên). Biết tam giác $A'BC$ vuông tại $A'$. Gọi $\varphi $ là góc giữa $\left( P \right)$ và $\left( {ABC} \right)$.
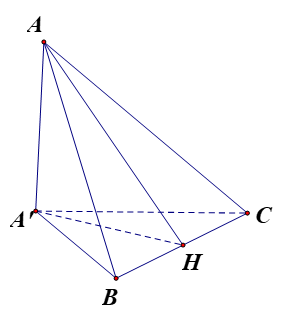
Chọn khẳng định đúng trong các khẳng định sau.
$\varphi = 60^\circ $.
$\varphi = 45^\circ $.
$\cos \varphi = \frac{{\sqrt 2 }}{3}$.
$\varphi = 30^\circ $.
