35 câu hỏi
Đổi số đo của góc $\alpha = 30^\circ $ sang rađian.
$\alpha = \frac{\pi }{2}.$
$\alpha = \frac{\pi }{4}.$
$\alpha = \frac{\pi }{6}.$
$\alpha = \frac{\pi }{3}.$
Cho $0 < \alpha < \frac{\pi }{2}.$ Khẳng định nào sau đây đúng?
$\cot \left( {\alpha + \frac{\pi }{2}} \right) > 0.$
$\cot \left( {\alpha + \frac{\pi }{2}} \right) \geqslant 0.$
$\tan \left( {\alpha + \pi } \right) < 0.$
$\tan \left( {\alpha + \pi } \right) > 0.$
Công thức nào dưới đây SAI?
$\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}$.
\[\cos a\cos b = \frac{1}{2}\left[ {{\text{cos}}\left( {a - b} \right) + {\text{cos}}\left( {a + b} \right)} \right]\].
\[\sin a\cos b = \frac{1}{2}\left[ {{\text{sin}}\left( {a - b} \right) + {\text{sin}}\left( {a + b} \right)} \right]\].
\[\sin a\sin b = \frac{1}{2}\left[ {{\text{cos}}\left( {a - b} \right) + {\text{cos}}\left( {a + b} \right)} \right]\].
Rút gọn $M = \sin \left( {x + y} \right)\cos y - \cos \left( {x + y} \right)\sin y$?
$M = \cos x$.
\[M = \sin x\].
$M = \sin \left( {x + 2y} \right)$.
$M = \cos \left( {x + 2y} \right)$.
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ.
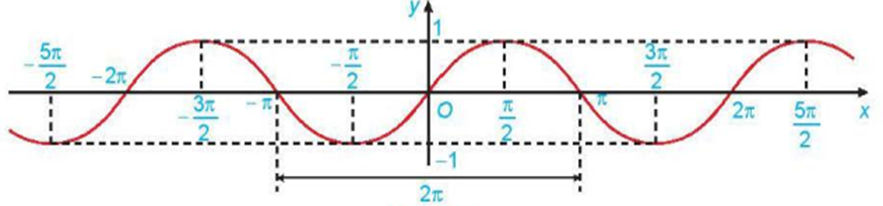
Đồ thị hàm số \[y = f\left( x \right)\]là đồ thị của hàm số nào dưới đây?
\[y = \tan x\].
\[y = \sin x\].
\[y = \cos x\].
\[y = \cot x\].
Trong các khẳng định sau, khẳng định nào sai ?
Tập xác định của hàm số \[y = \cot x\]là \[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}\,} \right\}\].
Tập xác định của hàm số \[y = \sin x\]là \[\mathbb{R}\].
Tập xác định của hàm số \[y = \cos x\]là \[\mathbb{R}\].
Tập xác định của hàm số \[y = \tan x\]là \[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}\,} \right\}\].
Trong các hàm số cho dưới đây, hàm số nào là hàm số tuần hoàn?
\[y = \tan x\].
\[y = {x^2} + \tan x\].
\[y = {x^2}\].
\[y = {x^2}\tan x\].
Phương trình $\tan x = \sqrt 3 $ có tập nghiệm là
\[\left\{ {\frac{\pi }{3} + k2\pi ,\,k \in \mathbb{Z}} \right\}\].
\[\emptyset \].
\[\left\{ {\frac{\pi }{3} + k\pi ,\,k \in \mathbb{Z}} \right\}\].
\[\left\{ {\frac{\pi }{6} + k\pi ,\,k \in \mathbb{Z}} \right\}\].
Nghiệm của phương trình $\cos x = - \frac{1}{2}$ là
$x = \pm \frac{{2\pi }}{3} + k2\pi $.
$x = \pm \frac{\pi }{6} + k\pi $.
$x = \pm \frac{\pi }{3} + k2\pi $.
$x = \pm \frac{\pi }{6} + k2\pi $.
Phương trình nào dưới đây tương đương với phương trình $x + 1 = 0$?
${x^2} - 1 = 0$.
$\frac{{x + 1}}{{x - 1}} = 0$.
${x^2} - 2x + 1 = 0$.
$\frac{{{x^2} + 2x + 1}}{{x + 1}} = 0$.
Cho dãy số \[\left( {{u_n}} \right)\] là dãy số tự nhiên lẻ theo thứ tự tăng dần và ${u_1} = 3$. Năm số hạng đầu của dãy số \[\left( {{u_n}} \right)\] là:
$1;3;5;7;9$.
$1,2,3,4,5$.
$3,5,7,9,11$.
$0,1,3,5,7$.
Cho dãy số \[\left( {{u_n}} \right)\] được xác định bởi \[\left\{ \begin{gathered}
{u_1} = 3 \hfill \\
{u_{n + 1}} = {u_n} - 2 \hfill \\
\end{gathered} \right.,\forall n \in {\mathbb{N}^*}\]. Khẳng định nào sau đây đúng?
$\left( {{u_n}} \right)$ là dãy số tăng.
$\left( {{u_n}} \right)$ là dãy số giảm.
$\left( {{u_n}} \right)$ không là dãy số tăng cũng không là dãy số giảm .
$\left( {{u_n}} \right)$ là dãy số không đổi.
Trong các dãy sốsau, dãy số nào là một cấp số cộng?
\[\;1; - 3; - 7; - 11; - 15; \cdots \]
\[1; - 3; - 6; - 9; - 12; \cdots \]
\[1; - 2; - 4; - 6; - 8; \cdots \]
\[1; - 3; - 5; - 7; - 9; \cdots \]
Cho dãy số \[\frac{1}{2};0; - \frac{1}{2}; - 1; - \frac{3}{2};.....\] là cấp số cộng với:
Số hạng đầu tiên là \[\frac{1}{2}\], công sai là \[\frac{1}{2}.\]
Số hạng đầu tiên là \[\frac{1}{2}\], công sai là \[ - \frac{1}{2}.\]
Số hạng đầu tiên là \[0\], công sai là \[\frac{1}{2}.\]
Số hạng đầu tiên là \[0\], công sai là \[ - \frac{1}{2}.\]
Dãy số nào sau đây không phải là cấp số nhân?
$1;{\text{ }}2;{\text{ }}4;{\text{ }}8;{\text{ }} \cdots $.
$3;{\text{ }}{3^2};{\text{ }}{3^3};{\text{ }}{3^4};{\text{ }} \cdots $.
$4;{\text{ }}2;{\text{ }}\frac{1}{2};{\text{ }}\frac{1}{4};{\text{ }} \cdots $.
$\frac{1}{\pi };{\text{ }}\frac{1}{{{\pi ^2}}};{\text{ }}\frac{1}{{{\pi ^4}}};{\text{ }}\frac{1}{{{\pi ^6}}};{\text{ }} \cdots $.
Cho cấp số nhân $\left( {{u_n}} \right)$ với ${u_1} = - 2$ và $q = - 5.$ Viết bốn số hạng đầu tiên của cấp số nhân.
$ - 2;{\text{ }}10;{\text{ }}50;{\text{ }} - 250.$
$ - 2;{\text{ }}10;{\text{ }} - 50;{\text{ }}250.$
$ - 2;{\text{ }} - 10;{\text{ }} - 50;{\text{ }} - 250.$
$ - 2;{\text{ }}10;{\text{ }}50;{\text{ }}250.$
Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao thông đang làm nhiệm vụ.
|
Tốc độ |
$\left[ {20;35} \right]$ |
$\left( {35;50} \right]$ |
$\left( {50;60} \right]$ |
$\left( {60;70} \right]$ |
$\left( {70;85} \right]$ |
$\left( {85;100} \right]$ |
|
Số phương tiện giao thông |
27 |
70 |
8 |
3 |
1 |
1 |
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
Số xe được đo tốc độ là 100 xe.
Mẫu số liệu đã cho gồm 5 nhóm có độ dài bằng nhau.
Tổng độ dài các nhóm là 80.
Số xe máy thuộc nhóm $\left[ {60;70} \right)$ là ít nhất.
Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả:
|
Chiều cao (cm) |
$\left[ {150;152} \right)$ |
$\left[ {152;154} \right)$ |
$\left[ {154;156} \right)$ |
$\left[ {156;158} \right)$ |
$\left[ {158;160} \right)$ |
$\left[ {160;162} \right)$ |
$\left[ {162;168} \right)$ |
|
Số học sinh |
5 |
18 |
40 |
25 |
8 |
3 |
1 |
Số học sinh có chiều cao từ 156 cm trở lên là
37.
77.
12.
25.
Cho bảng phân phối tần số ghép lớp:

Mệnh đề nào sau đúng là
Giá trị đại diện của lớp \[\left[ {50;52} \right)\]là \[53\].
Tần số của lớp \[\left[ {58;60} \right)\]là \[95\].
Tần số của lớp \[\left[ {52;54} \right)\]là \[35\].
Số \[50\] không phụ thuộc lớp \[\left[ {54;56} \right)\].
Nhóm chứa mốt của mẫu số liệu trong Câu 19 là
$\left[ {54;56} \right)$.
$\left[ {50;52} \right)$.
$\left[ {52;54} \right)$.
$\left[ {58;60} \right)$.
Cho $\cos \alpha = \frac{4}{5}$ với $0 < \alpha < \frac{\pi }{2}$. Tính $\sin \alpha $.
$\sin \alpha = \frac{1}{5}$.
$\sin \alpha = - \frac{1}{5}$.
$\sin \alpha = \frac{3}{5}$.
$\sin \alpha = \pm \frac{3}{5}$.
Rút gọn biểu thức \[A = \frac{{\sin x + \sin 2x + \sin 3x}}{{\cos x + \cos 2x + \cos 3x}}\].
\[A = \tan 6x.\]
\[A = \tan 3x.\]
\[A = \tan 2x.\]
\[A = \tan x + \tan 2x + \tan 3x.\]
Cho $\sin a = \frac{3}{5},\frac{\pi }{2} < a < \pi .$ Tính giá trị biểu thức $M = \sin \left( {a + \frac{\pi }{4}} \right)$.
$M = - \frac{{\sqrt 2 }}{{10}}$.
$M = - \frac{{\sqrt 2 }}{{10}}$.
$M = - \frac{{\sqrt 2 }}{{10}}$.
$M = - \frac{{\sqrt 2 }}{{10}}$.
Tìm giá trị lớn nhất \[M\]và giá trị nhỏ nhất \[m\]của hàm số \[y = 1 - 2\left| {{\text{cos}}3x} \right|\].
\[M = 3\,,\,m = - 1\].
\[M = 0\,,\,m = - 2\].
\[M = 1\,,\,m = - 1\].
\[M = 2\,,\,m = - 2\].
Hàm số \[f\left( x \right) = 2023\sin 3x\] tuần hoàn với chu kì bằng
\[2\pi \].
\[2023\pi \].
\[\frac{{2\pi }}{{2023}}\].
\[\frac{{2\pi }}{3}\].
Tất cả nghiệm của phương trình $\sin \left( {x - \frac{\pi }{5}} \right) = \sin \frac{{2\pi }}{5}$ là
$x = \frac{{3\pi }}{5} + k2\pi ,k \in \mathbb{Z}$.
$x = \frac{{4\pi }}{5} + k2\pi ,k \in \mathbb{Z}$.
$x = \frac{{2\pi }}{5} + k2\pi $ và $x = \frac{{3\pi }}{5} + k2\pi ,k \in \mathbb{Z}$.
$x = \frac{{3\pi }}{5} + k2\pi $ và $x = \frac{{4\pi }}{5} + k2\pi ,k \in \mathbb{Z}$.
Phương trình $\sin x = \cos x$ có số nghiệm thuộc đoạn $\left[ { - \pi ;\pi } \right]$ là
\[3\].
\[5\].
\[2\].
\[4\].
Biết năm số hạng đầu của dãy số$\left( {{u_n}} \right)$ là $1,\,2,2,4,8,32...$. Tìm một công thức truy hồi của dãy số trên.
$\left\{ \begin{gathered}
{u_1} = 1;\,{u_2} = 2 \hfill \\
{u_{n + 2}} = {u_{n + 1}}.{u_n} \hfill \\
\end{gathered} \right.,\forall n \in {\mathbb{N}^*}$.
$\left\{ \begin{gathered}
{u_1} = 1 \hfill \\
{u_{n + 1}} = 2.{u_n} \hfill \\
\end{gathered} \right.,\forall n \in {\mathbb{N}^*}$.
$\left\{ \begin{gathered}
{u_1} = 1 \hfill \\
{u_{n + 1}} = 4{u_n} - 2n \hfill \\
\end{gathered} \right.,\forall n \in {\mathbb{N}^*}$.
$\left\{ \begin{gathered}
{u_1} = 1;\,{u_2} = 2 \hfill \\
{u_{n + 2}} = 2{u_{n + 1}} - 2{u_n} \hfill \\
\end{gathered} \right.,\forall n \in {\mathbb{N}^*}$.
Cho dãy số \[\left( {{u_n}} \right)\] được xác định bởi \[\left\{ \begin{gathered}
{u_1} = 2 \hfill \\
{u_{n + 1}} = 3 + {u_n} \hfill \\
\end{gathered} \right.,\forall n \in \left\{ {1;2;3;4} \right\}\]. Tìm công thức số hạng tổng quát của \[\left( {{u_n}} \right)\].
${u_n} = 3n - 1$ với \[n \in \left\{ {1;2;3;4;5} \right\}\].
${u_n} = 3n - 1$ với \[n \in \left\{ {1;2;3;4} \right\}\].
${u_n} = {3^n}$ với \[n \in \left\{ {1;2;3;4} \right\}\].
${u_n} = {2^n}$ với \[n \in \left\{ {1;2;3;4;5} \right\}\].
Cho cấp số cộng $\left( {{u_n}} \right)$ biết \[{u_5} = 5\], \[{u_{10}} = 15\]. Khi đó \[{u_7}\] bằng
${u_7} = 12$.
${u_7} = 8$.
${u_7} = 7$.
${u_7} = 9$.
Tổng của bao nhiêu số hạng đầu của cấp số cộng $1; - 1; - 3;...$ bằng $ - 9800$.
${u_7} = 12$.
$99$.
\[101\].
\[98\].
Cho cấp số nhân có các số hạng lần lượt là $x;\,{\text{ }}12;\,{\text{ }}y;\,{\text{ }}192.$ Mệnh đề nào sau đây là đúng?
$x = 1;\,y = 144.$
$x = 2;\,y = 72.$
$x = 3;\,y = 48.$
$x = 4;\,y = 36.$
Cho cấp số nhân có các số hạng lần lượt là $3;\,{\text{ }}9;\,{\text{ }}27;\,{\text{ }}81;{\text{ }}...$. Tìm số hạng tổng quát ${u_n}$ của cấp số nhân đã cho.
${u_n} = {3^{n - 1}}.$
${u_n} = {3^n}.$
${u_n} = {3^{n + 1}}.$
${u_n} = 3 + {3^n}.$
Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Thời gian (giây) chạy trung bình cự li 1000 m của các bạn học sinh là
$130,35$.
$131,03$.
$130,4$.
$132,5$.
Trung vị của mẫu số liệu ghép nhóm trong Câu 34 là
${M_e} = \frac{{392}}{3}$.
${M_e} = \frac{{394}}{3}$.
${M_e} = \frac{{391}}{3}$.
${M_e} = \frac{{395}}{3}$.
