12 câu hỏi
Cho \(\frac{{7\pi }}{4} < \alpha < 2\pi \). Khẳng định nào sau đây đúng?
\(\cos \alpha > 0\).
\(\sin \alpha > 0\).
\(\tan \alpha > 0\).
\(\cot \alpha > 0\).
Khẳng định nào dưới đây sai?
\(\cos 2a = 2\cos a - 1\).
\(2{\sin ^2}a = 1 - \cos 2a\).
\(\sin \left( {a + b} \right) = \sin a\cos b + \sin b\cos a\).
\(\sin 2a = 2\sin a \cdot \cos a\).
Mệnh đề nào dưới đây đúng?
Hàm số \(y = \cot x\) là hàm số chẵn.
Hàm số \(y = \sin x\) là hàm số chẵn.
Hàm số \(y = \tan x\) là hàm số chẵn.
Hàm số \(y = \cos x\) là hàm số chẵn.
Tìm nghiệm của phương trình \(\cos x = - \frac{1}{2}.\)
\(x = \pm \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}.\)
\(x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}.\)
\(x = \pm \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}.\)
\(x = \pm \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}.\)
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{1}{3}\left( {{u_n} + 1} \right)\end{array} \right..\) Tìm số hạng \({u_3}.\)
\({u_3} = \frac{5}{9}.\)
\({u_3} = 1.\)
\({u_3} = \frac{2}{3}.\)
\({u_3} = \frac{{14}}{{27}}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\), biết \({u_1} = 2,{u_2} = 8\). Công sai của cấp số cộng là
\(d = 10\).
\(d = 6.\)
\(d = 4.\)
\(d = 16.\)
Dãy số nào sau đây là cấp số nhân?
\(1\), \( - 2\), \(4\), \( - 8\), \( - 16\).
\(2\), \(22\), \(222\), \(22222\).
\(3\), \(6\), \(12\), \(24\).
\(x\), \(2x\), \(3x\), \(4x\) với \(x \ne 0\).
Mệnh đề nào sau đây đúng?
Tứ diện có 4 mặt và 6 cạnh.
Tứ diện có 4 mặt và 4 cạnh.
Tứ diện có 4 mặt và 5 cạnh.
Tứ diện có 4 cạnh và 6 mặt.
Cho hình lập phương \(ABCD.EFGH\). Mệnh đề nào sau đây sai?
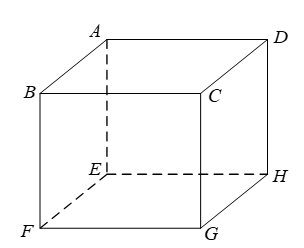
\(BG\) và \(HD\) chéo nhau.
\(BF\) và \(AD\) chéo nhau.
\(AB\) song song với \(HG\).
\(CG\) cắt \(HE\).
Biết \(\cos a = \frac{1}{3}\), \(\cos b = \frac{1}{4}\). Giá trị \[\cos \left( {a + b} \right) \cdot \cos \left( {a - b} \right)\] bằng
\[ - \frac{{113}}{{144}}.\]
\[ - \frac{{115}}{{144}}.\]
\[ - \frac{{117}}{{144}}.\]
\[ - \frac{{119}}{{144}}.\]
Cho cấp số cộng \(\left( {{u_n}} \right)\) biết \({u_1} = 4\) và \(d = 3\). Tổng \(S\) của \(20\) số hạng đầu tiên của cấp số cộng bằng bao nhiêu?
\({S_2}_0 = 750\).
\({S_2}_0 = 650\).
\({S_{20}} = 460\).
\({S_{20}} = 860\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành (xem hình vẽ). Khẳng định nào sau đây sai?
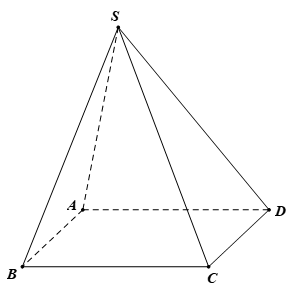
\(BC{\rm{//}}\left( {SAD} \right)\).
\(CD{\rm{//}}\left( {SAB} \right)\).
\(SA{\rm{//}}\left( {SCD} \right)\).
\(AD{\rm{//}}\left( {SBC} \right)\).
Gợi ý cho bạn
Xem tất cảĐề kiểm tra Cuối kì 1 Toán 11 Kết nối tri thức có đáp án
Đề kiểm tra Cuối kì 1 Toán 11 Kết nối tri thức có đáp án
Đề kiểm tra Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 02