30 câu hỏi
Kí hiệu S là diện tích hình phẳng gới hạn bởi đồ thị hàm số y = f (x) trục hoành và hai đường thẳng x = a, x = b như hình bên. Tìm khẳng định đúng?
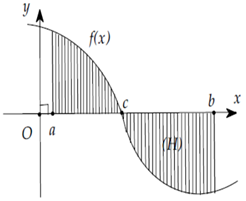
S =
S =
S =
S =
Cho hàm số f(x) thỏa mãn = 3. Tính tích phân ?
6
2
Tính tích phân bằng
-5
5
-10
10
Trong không gian oxyz , cho mặt cầu (S) có phương trình (x – 1)2 + (y – 2)2 + (z + 2)2 = 16. Tìm tọa độ tâm I và bán kính R của mặt cầu (S)?
I(−1; −2; 2), R = 16
I(1; 2; −2), R = 16
I(1; 2; −2), R =4
I(−1; −2; 2), R = 4
Giả sử H là hình phẳng giới hạn bởi đường y = f (x) liên tục trên đoạn [a; b], trục Ox và các đường thẳng x = a, x = b. Khi đó nếu H được xoay tròn quanh trục Ox sẽ tạo thành một khối có thể tích là:
V =
V =
V =
V =
Trong không gian Oxyz cho hai điểm A = (3; −2; 1), B = (1; 2; 3). Tính khoảng cách giữa hai điểm A và B?
Cho hàm số f(x) liên tục trên đoạn [a; b]. Hãy chọn khẳng định sai?
Cho hàm số f(x) = x − với x ≠ 0. Tìm khẳng định đúng?
Tìm thể tích của khối T tạo thành khi xoay hình H bao bởi đường y = x2 + 1, trục hoành và hai đường x = 0, x = 2 quanh trục Ox?
V =
V =
V =
V =
Tìm họ nguyên hàm của hàm số f(x) = cosx ?
sinx + C
cos2x + C
–sinx + C
–cosx + C
Kí hiệu S là diện tích hình phẳng gới hạn bởi các đồ thị hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b như hình bên. Tìm khẳng định sai?
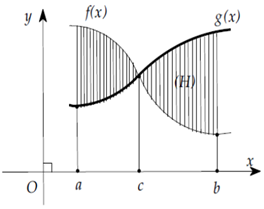
S =
S =
S =
S =
Giả sử một vật từ trạng thái nghỉ khi t = 0 chuyển động thẳng với vận tốc v(t) = t(5 − t) m/s . Tìm quãng đường vật đi dược cho tới khi nó dừng lại?
20,83 m
20,8 m
m
20,8333333 m
Diện tích của hình phẳng bao bởi đường y = sinx, trục Ox và hai đường thẳng x = − và x = bằng
3
2
1
5
Cho hàm số f(x) thỏa mãn = 20 và 3f(1) – 2f(0) = 7. Tính ?
-13
13
8
1
Cho hàm số f(x) = e2x – 1 . Tìm khẳng định đúng?
= 2e2x – 1 + C
= e2x – 1 + C
= e2x + C
= e2x – 1 + C
Tìm họ nguyên hàm của hàm số f (x) = x3 ?
4x4 + C
x4 + C
3x2 + C
x4 + C
Cho = 3. Tính tích phân ?
1
-1
Trong không gian Oxyz, mặt phẳng (P) đi qua A = (1; 0; 2) và song song với mặt phẳng (β) : 2x + 3y − z + 3 = 0 có phương trình là:
x + 2y – 3z + 5 = 0
2x + 3y – z – 1 = 0
2x + 3y – z = 0
2x + 3y – z + 1 = 0
Cho hàm số f(x) = xex biết F(x) là một nguyên hàm của f(x) và F(0) = 2. Khi đó F(x) bằng
F(x) = (x + 1)ex + 3
F(x) = (x + 4)ex – 2
F(x) = (x – 1)ex + 3
F(x) = −ex + 3
Tìm diện tích của hình phẳng nằm giữa các đường y = x và y = x3 – 3x ?
8
5
4
7
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong (C) trong hình vẽ bên , biết hàm số f(x) đạt cực trị tại hai điểm x1 , x2 thỏa x2 = x1 + 4 và = −12. Gọi d là đường thẳng đi qua hai điểm cực trị của đồ thị (C). Diện tích hình phẳng giới hạn bởi (C) và d bằng
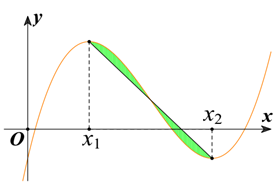
8
4
2
1
Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua điểm M = (3; −2; −2) nhận vectơ = (1; −2; 3) làm vectơ pháp tuyến?
x – 2y – 7 = 0
x – 2y – 3 z – 1 = 0
x – 2y + 3z – 1 = 0
3x – 2y – 2z – 1 = 0
Cho mặt phẳng ( Q ) có phương trình x – y + 3z − 1 = 0. Mặt phẳng (Q) đi qua điểm
M = (1; −2; −1)
M = (1; 3; 1)
M = (1; 1; 3)
M = (1; −1; −3)
Trong không gian Oxyz, cho hai vectơ = (1; −2; 3) và = (2; 5; −1). Tọa độ của vectơ là
(3; 3; 2)
(0; −9; 7)
(4; 1; 5)
(−1; −7; 4)
Trong không gian Oxyz, cho hai điểm A(1; 3; −2) và B(3; −1; 0). Phương trình mặt cầu đường kính AB là
(x – 2)2 + (y – 1)2 + (z + 1)2 =
(x – 4)2 + (y – 2)2 + (z + 2)2 = 24
(x – 2)2 + (y – 1)2 + (z – 1)2 = 6
(x + 2)2 + (y + 1)2 + (z – 1)2 = 6
Cho hàm số f(x) = liên tục trên R. Biết tích phân với là phân số tối giản. Giá trị của tổng a + b + c bằng
20
21
18
19
Một khối T với mặt cắt có diện tích là S(x) vuông góc với trục Ox tại mỗi điểm trên đoạn [a; b] có thể tích là:
V =
V =
V =
V =
Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng (Oxy) là
= (0; 1; 0)
= (1; 0; 0)
= (0; 0; 1)
= (1; 1; 0)
Trong không gian Oxyz, cho .Tọa độ điểm A là
A = (2; 3; −1)
A = (2; −1; 3)
A = (2; 1; 3)
A = (−1; 2; 3)
Trong không gian Oxyz, cho . Tọa độ của vectơ là
= (3; 4; −5)
= (4; −5; 3)
= (4; 3; 5)
= (4; 3; −5)
