Đề kiểm tra Dãy số (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Dãy số \(\left( {{u_n}} \right)\)nào sau đây là dãy số tăng?
\({u_n} = {3^{ - n}} + 1\).
\({u_n} = \sin n\).
\({u_n} = 2n - 3\).
\({u_n} = \frac{{n + 2}}{{n + 1}}\).
Cho dãy số \[\left( {{u_n}} \right)\] có \[{u_n} = \frac{1}{{n\left( {n + 1} \right)}}\]. Tìm mệnh đề đúng.
Dãy số \[\left( {{u_n}} \right)\] chỉ bị chặn dưới.
Dãy số \[\left( {{u_n}} \right)\] tăng.
Dãy số \[\left( {{u_n}} \right)\] bị chặn.
Dãy số \[\left( {{u_n}} \right)\] chỉ bị chặn trên.
Cho dãy số\(\left( {{u_n}} \right)\) với \({u_n} = \frac{{a{n^2}}}{{n + 1}}\) (\(a\) hằng số). Hỏi \({u_{n + 1}}\) là số hạng nào sau đây?
\({u_{n + 1}} = \frac{{a{n^2}}}{{n + 2}}\).
\({u_{n + 1}} = \frac{{a.{{\left( {n + 1} \right)}^2}}}{{n + 2}}\).
\({u_{n + 1}} = \frac{{a.{{\left( {n + 1} \right)}^2}}}{{n + 1}}\).
\({u_{n + 1}} = \frac{{a.{n^2} + 1}}{{n + 1}}\).
Cho dãy số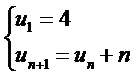 
. Năm số hạng đầu của dãy số là
\[4,\,5,\,6,\,7,\,8.\].
\[4,\,16,\,32,\,64,\,128.\].
\[4,\,6,\,9,\,13,\,18.\].
\[4,\,5,\,7,\,10,\,14.\]
Cho dãy số \(\left( {{u_n}} \right)\)xác định bởi \({u_1} = 3;\;{u_{n + 1}} = {u_n} + n,\;\forall \,n \in {\mathbb{N}^*}\). Giá trị \({u_1} + {u_2} + {u_3}\)bằng
\(18\).
\(13\).
\(15\).
\(16\).
Cho dãy số\(\left( {{u_n}} \right)\)xác định bởi:\(\left\{ \begin{array}{l}{u_1} = 2;{u_2} = 3\\{u_{n + 2}} = 3{u_{n + 1}} - 2{u_n}\end{array} \right.\)với\(n \ge 1\). Khẳng định nào sau đây sai?
\({u_n} = {2^{n - 1}} + 1\).
\(\left( {{u_n}} \right)\)là dãy số tăng.
Năm số hạng đầu của dãy số là:\(2\), \(3\), \(5\), \(9\), \(17\).
\({u_n} = \frac{{{n^2} + 5}}{3}\).
Cho dãy số \[\left( {{u_n}} \right)\]biết \[{u_n} = \frac{{{n^2} + 3}}{{2{n^2} - 1}}\] với \[n \in {N^*}\]. Tìm số hạng \[{u_5}\].
\[{u_5} = \frac{7}{4}.\].
\[{u_5} = \frac{7}{9}.\].
\[{u_5} = \frac{{24}}{{51}}.\].
\[{u_5} = \frac{4}{7}.\]
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \left( {a - 5} \right)n + 5 - a,\forall n \in \mathbb{N}*\). Dãy số \(\left( {{u_n}} \right)\)là dãy số giảm khi và chỉ khi
\[a \le 5\].
\[a \ge 5\].
\[a < 5\].
\[a > 5\].
Trong các dãy số \(\left( {{u_n}} \right)\) sau đây, dãy số nào bị chặn?
\({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{2n + 1}}\).
\({u_n} = n + \frac{1}{n}\).
\({u_n} = \sqrt {{n^2} + 1} \).
\({u_n} = {3.2^n}\).
Cho dãy số \(\left( {{u_n}} \right),\) được xác định \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = 2{u_n}\end{array} \right..\) Số hạng tổng quát \({u_n}\) của dãy số là số hạng nào dưới đây?
\({u_n} = {n^{n - 1}}.\)
\({u_n} = {2^n}.\)
\({u_n} = {2^{n + 1}}.\)
\({u_n} = 2.\)
Cho dãy số \[\left( {{u_n}} \right)\] với \[{u_n} = \sin \frac{\pi }{{n + 1}}\]. Khẳng định nào sau đây là đúng?
Dãy số \[\left( {{u_n}} \right)\] là một dãy số giảm.
Dãy số \[\left( {{u_n}} \right)\] là một dãy số tăng.
Số hạng thứ \[n + 1\] của dãy là \[{u_{n + 1}} = \sin \frac{\pi }{{n + 1}}\].
Dãy số \[\left( {{u_n}} \right)\] là dãy số không bị chặn.
Dãy số nào trong các dãy số sau đây là dãy số bị chặn?
\[\left( {{u_n}} \right),\,\,{u_n} = \frac{n}{{n + 1}}\,\,\,\forall n \in {\mathbb{N}^*}\].
\[\left( {{u_n}} \right),\,\,{u_n} = n + 1\,\,\,\forall n \in {\mathbb{N}^*}\].
\[\left( {{u_n}} \right),\,\,{u_n} = - n\,\,\,\,\forall n \in {\mathbb{N}^*}\].
\[\left( {{u_n}} \right),\,\,{u_n} = {n^2}\,\,\,\,\forall n \in {\mathbb{N}^*}\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = \frac{{2n + 1}}{{n + 2}}\). Khi đó:
a) Số hạng đầu tiên của dãy số là \(1\)
b) Số hạng \({u_2} = \frac{5}{4};{u_3} = \frac{7}{5}\)
c) Số hạng \({u_4} = \frac{3}{2};{u_5} = \frac{{11}}{7}\)
d) Số \(\frac{{167}}{{84}}\) là số hạng thứ 252 của dãy số \(\left( {{u_n}} \right)\)
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \ldots + \frac{1}{{n(n + 1)}}\). Khi đó:
a) Số hạng \({u_1} = \frac{1}{2}\)
b) Số hạng \({u_3} = \frac{3}{4}\)
c) \(\frac{{10}}{{11}}\) là số hạng thứ 11 của dãy số
d) \({u_{2023}} + {u_{2024}} > 2\)
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = n + \frac{1}{n}\). Khi đó:
a) \({u_{n + 1}} > {u_n},\forall n \in {\mathbb{N}^*}\)
b) Dãy số \(\left( {{u_n}} \right)\) là dãy số tăng
c) \({u_n} \ge 1,\forall n \in {\mathbb{N}^*}\)
d) Dãy số đã cho bị chặn trên
Bà Hoa gửi vào một ngân hàng số tiền 200 triệu đồng với lãi suất \(5\% \) một năm theo hình thức lãi kép, kì hạn 1 tháng. Số tiền (triệu đồng) của bà Hoa sau \(n\) tháng được tính theo công thức \({T_n} = 200{\left( {1 + \frac{{0,05}}{{12}}} \right)^n}\). Khi đó:
a) Sau 1 tháng, số tiền bà Hoa nhận được là khoảng \(200,83\) (triệu đồng)
b) Sau 2 tháng, số tiền bà nhận được là khoảng \(201,67\) (triệu đồng);
c) Sau 14 tháng, số tiền bà nhận được là khoảng \(211,99\) (triệu đồng).
d) Sau 17 tháng, số tiền bà nhận được là khoảng \(215,65\) (triệu đồng).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Xét tính bị chặn của dãy số \(\left( {{u_n}} \right)\), với \({u_n} = 2n - 1\).
Cho dãy số \(({u_n})\) được xác định như sau: \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + 2\end{array} \right.\). Tìm số hạng \({u_{50}}\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_1} = 1\) và \({u_{n + 1}} = 3{u_n} + 10\) với mọi \(n \ge 1.\)
Chứng minh rằng:
Xét tính tăng, giảm của dãy số \(\left( {{u_n}} \right)\), với \({u_n} = \frac{1}{{n + 1}}\).
Chứng minh rằng dãy số \(\left( {{u_n}} \right)\), với \({u_n} = \frac{{{n^2} + 1}}{{2{n^2} - 3}}\) là một dãy số bị chặn.
Ông An gửi tiết kiệm 100 triệu đồng kì hạn 1 tháng với lãi suất \(6\% \) một năm theo hình thức tính lãi kép. Số tiền (triệu đồng) của ông An thu được sau \(n\) tháng được cho bởi công thức \({A_n} = 100{\left( {1 + \frac{{0,06}}{{12}}} \right)^n}{\rm{. }}\)
a) Tìm số tiền ông An nhận được sau tháng thứ nhất, sau tháng thứ hai.
b) Tìm số tiền ông An nhận được sau 1 năm.
