Đề kiểm tra Dãy số (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_1} = 2\) và \({u_n} = \frac{{{u_{n - 1}} + 1}}{2}\) với mọi \(n \ge 2\). Ba số hạng đầu tiên của dãy số lần lượt là:
\(2;1;\frac{3}{2}\).
\(2;\frac{3}{2};\frac{5}{2}\).
\(2;\frac{3}{2};\frac{5}{4}\).
\(2;\frac{3}{2};2\).
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = {3^n}\). Số hạng \({u_{n + 1}}\) bằng:
\({3^n}.3\).
\({3^n} + 3\).
\({3^n} + 1\).
\(3(n + 1)\).
Trong các dãy số \(\left( {{u_n}} \right)\) được xác định như sau, dãy số giảm là:
\({u_n} = \frac{{3n - 1}}{{n + 1}}\).
\({u_n} = {n^3}\).
\({u_n} = \frac{1}{{{3^{n + 1}}}}\).
\({u_n} = \sqrt n \).
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \cos n\). Dãy số \(\left( {{u_n}} \right)\) là:
Dãy số tăng.
Dãy số giảm.
Dãy số bị chặn.
Dãy số bị chặn dưới, không bị chặn trên.
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_n} = \frac{{{2^{n - 1}} + 1}}{n}\). Tìm số hạng thứ \(10\) của dãy số đã cho.
\(51,2\).
\(51,3\).
\(51,1\).
\(102,3\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = {\left( { - 1} \right)^{n + 1}}\sqrt {n + 1} \). Mệnh đề nào sau đây đúng?
\({u_8} = 3\).
\({u_8} = - 3\).
\({u_8} = \sqrt 8 \).
\({u_8} = - \sqrt 8 \).
Cho dãy số \(\left( {{u_n}} \right)\) cho bởi công thức tổng quát \({u_n} = 3 + 4{n^2},\,\,n \in {\mathbb{N}^*}\). Khi đó \({u_5}\) bằng
\(103\).
\(23\).
\(503\).
\( - 97\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {3^n}.\) Tính \({u_{n + 1}}?\)
\({u_{n + 1}} = {3^n} + 3.\).
\({u_{n + 1}} = {3.3^n}.\).
\({u_{n + 1}} = {3^n} + 1.\).
\({u_{n + 1}} = 3\left( {n + 1} \right).\)
Trong các dãy số sau, dãy số nào là dãy số giảm?
\[{u_n} = {n^2}\].
\[{u_n} = 2n\].
\[{u_n} = {n^3} - 1\].
\[{u_n} = \frac{{2n + 1}}{{n - 1}}\].
Cho dãy số \(\left( {{u_n}} \right)\)với \({u_n} = 2n - 1\). Dãy số \(\left( {{u_n}} \right)\)là dãy số
Bị chặn trên bởi 1.
Giảm.
Bị chặn dưới bởi 2.
Tăng.
Cho dãy số \(\left( {{u_n}} \right)\)với \({u_n} = \frac{1}{{n + 2}}\). Trong các mệnh đề dưới đây, mệnh đề nào đúng?
Dãy số \(\left( {{u_n}} \right)\)là dãy số giảm và bị chặn.\(\).
Dãy số \(\left( {{u_n}} \right)\)là dãy số tăng và bị chặn trên.
Dãy số \(\left( {{u_n}} \right)\)là dãy số giảm và không bị chặn dưới.
Dãy số \(\left( {{u_n}} \right)\)là dãy số tăng và không bị chặn trên.
Cho dãy số \(\left( {{U_n}} \right)\) có số hạng tổng quát \({U_n} = \frac{{n - 1}}{{n + 2}},\left( {n \in {N^*}} \right)\). Số hạng thứ \(100\) của dãy số là
\({U_{100}} = \frac{{33}}{{34}}.\).
\({U_{100}} = \frac{{37}}{{34}}.\).
\({U_{100}} = \frac{{39}}{{34}}.\).
\({U_{100}} = \frac{{35}}{{34}}.\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{ - n}}{{n + 1}}\). Khi đó:
a) Năm số hạng đầu tiên của dãy số là \({u_1} = - \frac{1}{2};{u_2} = - \frac{2}{3};{u_3} = - \frac{3}{4};{u_4} = - \frac{4}{5};{u_5} = - \frac{5}{6}\)
b) Số hạng \({u_{10}},{u_{100}}\) lần lượt là \( - \frac{{10}}{{11}}; - \frac{{100}}{{101}}\)
c) \( - \frac{{85}}{{86}}\) là số hạng thứ 86 của dãy số \(\left( {{u_n}} \right)\)
d) \( - \frac{{99}}{{101}}\) là một số hạng của dãy số \(\left( {{u_n}} \right)\)
Cho dãy số \(\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{l}}{{u_1} = 2023;{u_2} = 2024}\\{2{u_{n + 1}} = {u_n} + {u_{n + 2}}}\end{array}} \right.\) với \(n \ge 1\). Khi đó:
a) Dãy \(\left( {{v_n}} \right):{v_n} = {u_n} - {u_{n - 1}}\) là dãy không đổi.
b) Biểu thị \({u_n}\) qua \({u_{n - 1}}\) ta được \({u_n} = {u_{n - 1}} + 1\)
c) Ta có \({u_3} = 2025\)
d) Ta có \({u_{2024}} = 4044\)
Cho dãy số \(\left( {{u_n}} \right)\) được xác định \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 2}\\{{u_{n + 1}} - {u_n} = 2n - 1}\end{array}} \right.\). Khi đó:
a) Ta có \({u_2} = 3\)
b) Ta có \({u_4} = 11\)
c) Ta có \({u_{2024}} = 4092536\)
d) Ta có \({u_{2023}} = 4088482\)
Cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = \sqrt {n + 1} - \sqrt n \). Khi đó:
a) \(\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{\sqrt {n + 2} + \sqrt n }}{{\sqrt {n + 3} + \sqrt {n + 2} }}\)
b) \(\frac{{{u_{2024}}}}{{{u_{2023}}}} < 1\)
c) \({u_{n + 1}} < {u_n},\forall n \in {\mathbb{N}^*}\)
d) Dãy số \(\left( {{u_n}} \right)\) là dãy số giảm.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tính tổng 6 số hạng đầu của dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = 3n - 1\).
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_1} = 2\) và \({u_n} = \sqrt {2 + u_{n - 1}^2} \) với mọi \(n \ge 2\). Viết năm số hạng đầu của dãy số và dự đoán công thức của số hạng tổng quát \({u_n}\).
Dự đoán công thức số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\) , biết \(\left\{ \begin{array}{l}{u_1} = - 2\\{u_{n + 1}} = - 2 - \frac{1}{{{u_n}}}\end{array} \right.\)
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 4}\\{{u_{n + 1}} = {u_n} + n}\end{array}(n \ge 1)} \right.\).
Tìm số hạng thứ năm của dãy số đó.
Với mỗi số nguyên dương \(n\), lấy \(n + 6\) điểm cách đều nhau trên đường tròn. Nối mỗi điểm với điểm cách nó hai điểm trên đường tròn đó để tạo thành các ngôi sao như Hình 1. Gọi \({u_n}\) là số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao thì ta được dãy số \(\left( {{u_n}} \right)\).
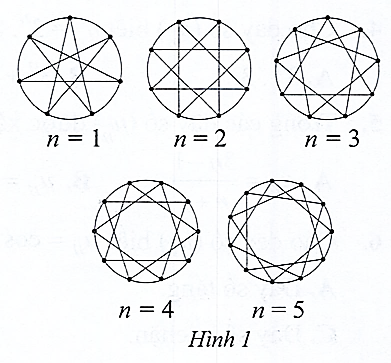
Tìm công thức của số hạng tổng quát \({u_n}\).
Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn \(75\% \) giá trị trong năm liền trước đó. Tính giá trị còn lại của chiếc máy photocopy đó sau mỗi năm, trong khoảng thời gian 5 năm kể từ khi mua.








