Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 9

2.1. Tính giá trị của biểu thức \(A = \frac{{x - 2y - z}}{2}\) với \(x = - 1;y = 1;z = - 1\).

2.2. Cho đa thức \(A\left( x \right) = \frac{3}{4}{x^3} - 1 + \frac{3}{5}x + 4{x^2} + \frac{5}{4}{x^3} - \frac{8}{5}x + 4 + 7{x^2}\).

     a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.

     b) Tính giá trị của \(A\left( x \right)\) tại \(x = - 1\).

     c) Tìm đa thức \(C\left( x \right)\) sao cho \(B\left( x \right) - C\left( x \right) = A\left( x \right)\), biết \(B\left( x \right) = 2{x^3} + 12{x^2} - 3x + 3\). Tìm nghiệm của đa thức \(C\left( x \right)\).

Trong một thùng đựng \(20\) quả bóng được đánh số \(5;6;7;....;23;24\). Lấy ngẫu nhiên một quả bóng.

     a) Viết tập hợp \(M\) gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra.

     b) Tính xác suất của biến cố \(N\): “Quả bóng lấy ra là số lẻ”.

     c) Tính xác suất của biến cố \(P\) : “Quả bóng lấy ra là ước của \(48\)”.

Nhóm của An tổ chức đi dã ngoại, các bạn dự định dựng một cái lều trên bãi có dạng hình lăng trụ đứng tam giác với kích thước như hình bên.

a) Tính thể tích khoảng không bên trong lều.

b) Biết rằng phủ vải bốn phía, trừ mặt trên cỏ. Tính diện tích bạt cần phải có để đựng lều.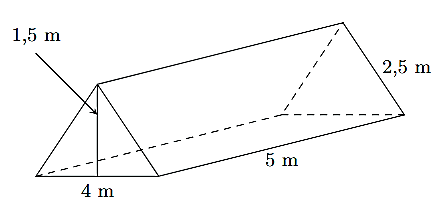 

Cho \(\widehat {xOy}\) là góc nhọn. Trên tia \(Ox\) lấy điểm \(A\) (\(A \ne O\)). Trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA = OB\). Từ \(A\) kẻ đường thẳng vuông góc với \(OA\), cắt \(Oy\) tại \(E\). Từ \(B\) kẻ đường thẳng vuông góc với \(OB\), cắt \(Ox\) tại \(F\).

     a) Chứng minh \(\Delta OAE = \Delta OBF\), từ đó suy ra \(OE = OF\).

     b) Gọi \(I\) là giao điểm của \(AE\) và \(BF\). Gọi \(M\) là trung điểm của \(EF\). So sánh \(EM\) và \(\frac{{EI + IF}}{2}.\)

     c) Chứng minh ba điểm \(O\), \(I\), \(M\) thẳng hàng.

Một công ty may có \(104\) công nhân được chia làm ba tổ. Nếu tổ I bớt đi 1 công nhân, tổ II bớt đi 2 công nhân, tổ III thêm vào 3 công nhân thì số công nhân trong các tổ I, II, III lần lượt tỉ lệ nghịch với \(3;4;2\). Tính số công nhân của mỗi tổ.