Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 5
29 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Giá trị của \(x\) thỏa mãn tỉ lệ thức \(\frac{{15}}{x} = \frac{3}{2}\) là
\(x = 12.\)
\(x = 6.\)
\(x = 30.\)
\(x = 10.\)
Biết rằng \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k = 3.\) Khi đó, phát biểu nào sau đây là sai?
\(y = 3x.\)
\(y = \frac{3}{x}.\)
\(x = \frac{1}{3}y.\)
\(\frac{y}{x} = 3.\)
Biểu thức đại số biểu thị nửa tổng của \(x\) và \(y\) là
\(x + y.\)
\(\frac{x}{2} + y.\)
\(\frac{{x + y}}{2}.\)
\(x + \frac{y}{2}.\)
Đa thức một biến nào sau đây có hệ số tự do bằng 2?
\({x^2} + 2xy - 2.\)
\({x^3} + 2xy + 2.\)
\(2{x^2} - 5x + 1.\)
\( - {x^2} + 3x + 2.\)
Kết quả của phép nhân hai đa thức \(\left( {2x - 3} \right)\left( {2x + 3} \right)\) là
\(4{x^2} + 12x + 9.\)
\(4{x^2} - 9.\)
\(2{x^2} - 3.\)
\(4{x^2} + 9.\)
Một thùng kín đựng 7 quả bóng đỏ, 12 quả bóng màu xanh, 18 quả bóng màu vàng, 15 quả bóng màu trắng có cùng kích thước. Nam lấy ngẫu nhiên một quả bóng trong thùng. Hỏi khả năng Nam lấy được quả bóng màu nào lớn nhất?
Đỏ
Xanh.
Vàng.
Trắng.
Gieo một con xúc xắc cân đối. Xét các biến cố sau, biến cố nào là biến cố chắc chắn?
“Mặt xuất hiện có số chấn nhỏ hơn 7”.
“Mặt xuất hiện có số chấm chia hết cho 7”.
“Mặt xuất hiện có số chấm lớn hơn 4”.
“Mặt xuất hiện có số chấm nhỏ hơn 2”.
Cho \(\Delta ABC\) có \(\widehat B = 70^\circ ,\widehat A = 50^\circ \). Khẳng định nào sau đây là đúng?
\(AB > BC > AC.\)
\(AC > AB > BC.\)
\(BC > AB > AC.\)
\(AC > BC > AB.\)
Cho \(\Delta ABC\) có \(I\) là giao điểm của ba đường phân giác trong \(\Delta ABC\). Khi đó, ta có:
\(AI\) vuông góc với \(BC.\)
\(I\) cách đều ba đỉnh của \(\Delta ABC\).
\(\Delta ABI\) cân ở \(I.\)
\(I\) cách đều ba cạnh của \(\Delta ABC\).
Vịnh Hạ Long là một trong bảy kì quan thiên nhiên của thế giới, giả sử 3 hòn núi đá tạo thành một tam giác, người ta muốn xây dựng một cột đèn để chiếu sáng cả ba hòn núi trên sao cho cột đèn cách đều ba điểm được đánh dấu trên hòn núi đá. Khi đó vị trí cột đèn sẽ nằm ở:
Trọng tâm của tam giác.
Trực tâm của tam giác.
Giao điểm của ba đường phân giác của tam giác.
Giao điểm của ba được trung trực của tam giác.
Số cạnh của một hình hộp chữ nhật là
4.
6.
8.
12.
Phát biểu nào sau đây là đúng?
Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
Các mặt bên của hình lăng trụ đứng là các hình thang cân.
Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
Các mặt bên của hình lăng trụ đứng là các hình bình hành.
a) Biến cố “Thẻ rút được là số nguyên tố” là biến cố chắc chắn.
b) Biến cố “Thẻ rút được là ước của \(72\)” là biến cố ngẫu nhiên.
c) Xác suất của biến cố “Thẻ rút được là bội của \(2\)” là \(\frac{1}{2}.\)
d) Xác suất của biến cố “Thẻ rút được là số chia \(3\) dư \(2\)” là \(\frac{2}{3}\).
a) \(AE = BD.\)
b) \(DE\parallel AB.\)
c) \(IM\) vuông góc với \(AB.\)
d) \(AB + 2BC < CI + 2AE.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một ô tô chạy từ A đến B với vận tốc \(72{\rm{ km/h}}\) thì mất \(5\) giờ. Hỏi chiếc ô tô đó chạy từ A đến B với vận tốc \({\rm{60 km/h}}\) thì mất khoảng bao nhiêu thời gian? (Đơn vị: giờ)
Tìm nghiệm của đa thức \(M\left( x \right) = 3x\left( {2x + 1} \right) + \left( {2 - x} \right)\left( {6x + 3} \right)\).
(Kết quả ghi dưới dạng số thập phân)
Cho đa thức \(h\left( x \right) = {x^3} + 3{x^2} + 5x + m\) (\(m\) là hệ số). Tìm \(m\) để đa thức chia hết cho \(x + 1.\)
Một khối gỗ hình hộp chữ nhật có kích thước \(20{\rm{ cm, 12 cm, 10 cm}}\) như hình vẽ.
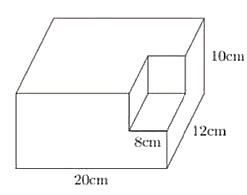
Người ta cắt đi một phần khối gỗ hình lập phương cạnh \({\rm{8 cm}}\). Tính thể tích phần còn lại của khối gỗ.
(Đơn vị: cm3).
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Hai xe máy cùng đi từ A đến B. Xe thứ nhất đi hết \(1\) giờ 20 phút, xe thứ hai đi hết 1 giờ 30 phút. Tính vận tốc trung bình của mỗi xe, biết rằng vận tốc trung bình của xe thứ nhất lớn hơn vận tốc trung bình của xe thứ hai là \(6{\rm{ km/h}}\).
a) Chứng minh \(\Delta ABH = \Delta ACH.\) Từ đó suy ra \(AH\) vuông góc với \(BC\).
b) Tia phân giác của góc \(B\) cắt \(AH\) tại \(I.\) Chứng minh tam giác \(BIC\) cân.
c) Đường thẳng đi qua \(A\) và song song với \(BC\) cắt \(BI,CI\) lần lượt tại \(M,N\). Chứng minh \(A\) là trung điểm của đoạn \(MN.\)
(0,5 điểm) Trong một hộp gỗ có các thẻ được đánh số từ \(100\) đến \(1{\rm{ }}000\). Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất để thẻ rút ra chia hết cho \(17.\)








