Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
29 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Từ \(2.4 = \left( { - 1} \right).\left( { - 8} \right)\), ta có tỉ lệ thức
\(\frac{{ - 1}}{2} = \frac{4}{{ - 8}}.\)
\(\frac{2}{4} = \frac{1}{8}.\)
\(\frac{4}{2} = \frac{8}{1}.\)
\(\frac{2}{{ - 1}} = \frac{4}{{ - 8}}.\)
Biết \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ là \(a\) và khi \(x = 4\) thì \(y = - 8\). Hệ số tỉ lệ của \(a\) là
\( - 12.\)
\( - 32.\)
\( - 2.\)
\(\frac{{ - 1}}{2}.\)
Bậc của đa thức \(11{x^{10}} + x + 5{x^3} - 3{x^4} - 11{x^{10}} - 3{x^5} - 6\) là
\(3.\)
\(4.\)
\(5.\)
\(9.\)
Kết quả của phép tính \(\frac{1}{6}{x^3}.{\left( { - 2x} \right)^2}\) là
\( - \frac{2}{3}{x^5}.\)
\(\frac{2}{3}{x^5}.\)
\( - \frac{2}{3}{x^6}.\)
\(\frac{2}{3}{x^6}.\)
Viết một đa thức một biến có hai hạng tử mà hệ số cao nhất là \(5\) và hệ số tự do là \( - 1.\)
\( - {x^2} + 5.\)
\(5{x^2} - x.\)
\(5{x^3} - 1.\)
\(5{x^2} - x - 1.\)
Đáp án đúng nhất khi nói về giá trị của xác suất \(P\) của một biến cố là
\(0 < P < 1.\)
\(0 < P \le 1.\)
\(0 \le P \le 1.\)
\(0 \le P < 1.\)
Rút ngẫu nhiên một quả bóng bán từ một chiếc hộp đựng 9 quả bóng có đánh số: \(0;1;2;3;\)\(4;5;6;7;8;9\). Biến cố “Rút được quả bóng có ghi số 9” là biến cố gì?
Biến cố chắc chắn.
Biến cố ngẫu nhiên.
Biến cố không thể.
Biến cố đã xảy ra.
Cho tam giác \(ABC\) có \(\widehat B\) là góc tù và \(\widehat A > \widehat C\). Khẳng định nào sau đây là đúng?
\(AC > AB > BC.\)
\(BC > AB > AC.\)
\(AB > AC > BC.\)
\(AC > BC > AB.\)
Cho \(I\) là giao điểm của ba đường phân giác trong của một tam giác. Kết luận nào sau đây là đúng?
\(I\) cách đều ba cạnh của tam giác.
\(I\) cách đều ba đỉnh của tam giác.
\(I\) là trọng tâm của tam giác.
\(I\) cách đỉnh một khoảng bằng \(\frac{2}{3}\) độ dài đường phân giác.
Bạn Bình đã lấy một miếng bìa hình tam giác và đặt đầu nhọn của chiếc bút chì vào điểm \(H\) trên hình tam giác thì mấy miếng bìa cân bằng trên đầu bút. Hỏi bạn Bình đã xác định vị trí điểm \(H\) bằng cách nào?
Bạn Bình vẽ hai đường trung trực cắt nhau tại \(H.\)
Bạn Bình vẽ hai đường cao cắt nhau tại \(H.\)
Bạn Bình vẽ hai đường trung tuyến cắt nhau tại \(H.\)
Bạn Bình vẽ hai đường phân giác cắt nhau tại \(H.\)
Trong các hình sau, đâu là hình lăng trụ đứng tam giác?
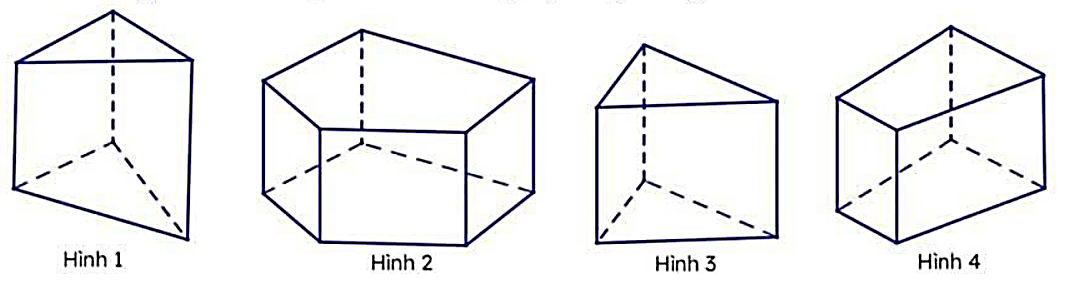
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Hình hộp chữ nhật có ba kích thước lần lượt là \(a;2a;\frac{a}{2}\). Thể tích của hình hộp chữ nhật đó là
\({a^2}.\)
\(4{a^2}.\)
\({a^3}.\)
\(2{a^3}.\)
a) Biến cố “Mặt xuất hiện có số chấm nhỏ hơn 8” là biến cố chắc chắn.
b) Biến cố “Mặt xuất hiện có số chấm chia hết cho 7” là biến cố ngẫu nhiên.
c) Xác suất của biến cố “Mặt xuất hiện có số chấm không nhỏ hơn 3” là \(\frac{1}{2}.\)
d) Xác suất của biến cố “Mặt xuất hiện có số chấm là số chia 4 dư 2” là \(\frac{1}{3}.\)
a) \(\widehat {ACB} = 60^\circ \).
b) \(\Delta ABE = \Delta EBH\).
c) \(BE\) là phân giác của \(\widehat B\).
d) \(BE\) vuông góc với \(KC.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Dùng \(8\) máy thì tiêu thụ hết \(70\) lít xăng. Hỏi dùng \(12\) máy thì số xăng tiêu thụ là bao nhiêu lít?
Tìm giá trị của \(m\) biết đa thức \(f\left( x \right) = 2{x^2} + mx + 6\) có nghiệm \(x = - 2.\)
Có bao nhiêu giá trị nguyên của \(x\) để giá trị của đa thức \(k\left( x \right) = {x^3} - {x^2} - x + 3\) chia hết cho giá trị của đa thức \(s\left( x \right) = x - 2.\)
Một ngôi nhà đồ chơi có kích thước như hình dưới dây.
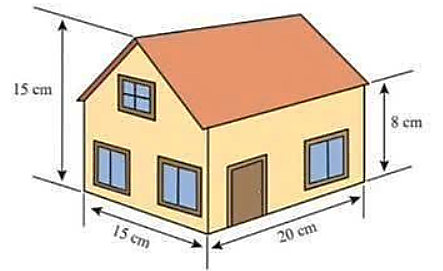
Hỏi thể tích của ngôi nhà là bao nhiêu? (Đơn vị: cm3)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Ba đội máy cày trên ba cánh đồng có diện tích như nhau. Đội I hoàn thành công việc trong 3 ngày, đội II trong 5 ngày, đội III trong 6 ngày. Hỏi mỗi đội có bao nhiêu máy cày, biết rằng đội II nhiều hơn đội III 1 máy và công suất các máy là như nhau.
a) Chứng minh \(DE \bot BC\) và \(BD\) là đường trung trực của đoạn thẳng \(AE.\)
b) So sánh \(DA\) và \(DC.\)
c) Hạ \(CF\) vuông góc với tia \(BD\) tại \(F\). Chứng minh ba đường thẳng \(AB,DE,CF\) đồng quy.
(0,5 điểm) Chọn ngẫu nhiên một số có hai chữ số. Tính xác suất để số được chọn chia hết cho \(2\) mà không chia hết cho \(5\).








