Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 10
6 câu hỏi
1.1. Tìm \(x,\)biết:
a) \(\frac{x}{3} = \frac{{ - 10}}{6};\) b) \(\frac{{2 - x}}{4} = \frac{{x - 3}}{{ - 5}}\).
1.2. Ba đội y tế tiêm ngừa vaccine Covid – 19 tại ba trường THCS trong quận có cùng số lượng học sinh đăng kí tiêm chủng như nhau. Đội thứ nhất tiêm xong trong 5 ngày, đội thứ hai tiêm xong trong 4 ngày và đội thứ ba tiêm xong trong 6 ngày. Hỏi mỗi đội có bao nhiêu cán bộ y tế, biết cả ba đội có tất cả 37 cán bộ? (Năng suất làm việc của các cán bộ y tế là như nhau)
2.1. Tính giá trị của biểu thức \(H = xy - xz + yz\) tại \(x = - 1;y = 1;z = - 1\).
2.2. Cho đa thức \(A\left( x \right) = \frac{5}{6}{x^3} - \frac{{12}}{7}{x^2} + 5x + \frac{5}{7}{x^2} + \frac{1}{6}{x^3} - 3x + 9\).
a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Xác định hệ số tự do của đa thức \(A\left( x \right)\) và tính \(A\left( 2 \right)\).
c) Tìm đa thức \(C\left( x \right)\) sao cho \(A\left( x \right) + C\left( x \right) = B\left( x \right)\), biết \(B\left( x \right) = {x^3} - 2{x^2} + 9x - 3\). Tìm nghiệm của đa thức \(C\left( x \right)\).
Trong hộp gỗ gồm 6 thẻ gỗ cùng loại, được đánh số \(12;13;14;15;16;17\) rút ngẫu nhiên một thẻ.
a) Viết tập hợp \(A\) gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra.
b) Tính xác suất của biến cố \(B\): “Thẻ rút được là ước của 24”.
c) Tính xác suất của biến cố \(C\): “Thẻ rút được chia 3 dư 2”.
Một các bục hình lăng trụ đứng có kích thước như hình bên.
a) Tính thể tích của cái bục.
b) Người ta muốn sơn tất cả các mặt của cái bục. Biết rằng giá sơn là \(15{\rm{ 000}}\) đồng/m2. Tính số tiền cần trả để sơn các mặt của bục đó.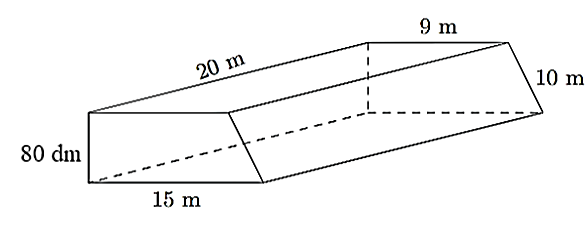
Cho \(\Delta ABC\) cân tại \(A\) (\(\widehat A < 90^\circ \)). Kẻ \(BD \bot AC\) tại \(D\) và \(CE \bot AB\) tại \(E\).
a) Chứng minh \(\Delta ABD = \Delta ACE\), từ đó suy ra \(\widehat {ABD} = \widehat {ACE}\).
b) Gọi \(H\) là giao điểm của \(BD\) và \(CE\).
Chứng minh \(\Delta BHC\) là tam giác cân. So sánh \(HB\) và \(HD.\)
c) Trên tia đối của tia \(EH\), lấy điểm \(P\) sao cho \(PH < HC\). Trên tia đối của tia \(DH\), lấy điểm \(Q\) sao cho \(QH = HP\). Chứng minh các đường thẳng \(BP\), \(AH\), \(CQ\) đồng quy.
Một cửa hàng có ba loại vải với tổng chiều dài là \(186{\rm{ m}}\). Giá tiền của mỗi mét vải của ba loại là như nhau. Sau khi bán được một ngày, cửa hàng còn lại \(\frac{2}{3}\) cuộn vải loại I, \(\frac{1}{3}\) cuộn vải loại II và \(\frac{3}{5}\) cuộn vải loại III. Số tiền bán được mỗi loại vải của cửa hàng lần lượt tỉ lệ với \(2;3;2\). Tính xem trong ngày đó cửa hàng đã bán được bao nhiều mét vải của mỗi loại?








