Đề kiểm tra Bài tập cuối chương 1 (có lời giải) - Đề 5
22 câu hỏi
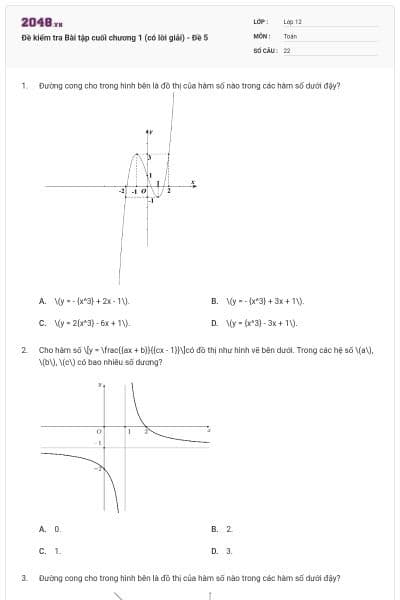
Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đậy? 
\(y = - {x^3} + 2x - 1\).
\(y = - {x^3} + 3x + 1\).
\(y = 2{x^3} - 6x + 1\).
\(y = {x^3} - 3x + 1\).
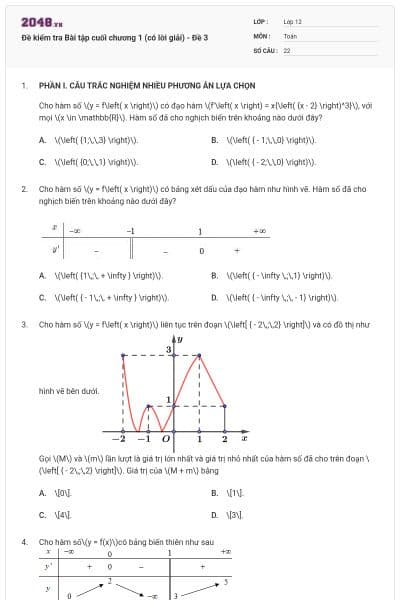
Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\]có đồ thị như hình vẽ bên dưới. Trong các hệ số \(a\), \(b\), \(c\) có bao nhiêu số dương?![Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\] có đồ thị như hình vẽ bên dưới. Trong các hệ số \(a\), \(b\), \(c\) có bao nhiêu số dương? A. 0. B. 2. C. 1. D. 3. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759228513.png)
0.
2.
1.
3.
Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đậy?
\[y = \frac{{{x^2} - 2x + 2}}{{x + 1}}\].
\[y = \frac{{ - {x^2} + x + 2}}{{x - 1}}\].
\[y = \frac{{{x^2} - x + 1}}{{ - x + 1}}\].
\[y = \frac{{ - {x^2} - x + 1}}{{x - 1}}\].
Cho hàm số \[y = \frac{{a{x^2} + bx + 1}}{{cx + 2}}\]có đồ thị như hình vẽ bên dưới. Tính giá trị biểu thức: \(T = 2a + 3b - c\).![Cho hàm số \[y = \frac{{a{x^2} + bx + 1}}{{cx + 2}}\] có đồ thị như hình vẽ bên dưới. Tính giá trị biểu thức: \(T = 2a + 3b - c\). A. 9. B. 10. C. 8. D. 11. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/4-1759228607.png)
9.
10.
8.
11.
Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau:![Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau: Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. \[\left( {2; + \infty } \right)\]. B. \[\left( {0;2} \right)\]. C. \[\left( { - 3;1} \right)\]. D. \[\left( { - \infty ;1} \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/5-1759228658.png)
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\[\left( {2; + \infty } \right)\].
\[\left( {0;2} \right)\].
\[\left( { - 3;1} \right)\].
\[\left( { - \infty ;1} \right)\].
Hàm số \[y = - {x^3} + 3{x^2}\] đồng biến trên khoảng nào dưới đây?
\[\left( {0;4} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {2; + \infty } \right)\].
\[\left( {0;2} \right)\]
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ { - 2\,;\,2} \right]\) và có đồ thị là đường cong trong hình vẽ sau.![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ { - 2\,;\,2} \right]\) và có đồ thị là đường cong trong hình vẽ sau. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/6-1759228731.png)
Điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) là
\[x = 1\].
\[x = - 2\].
\[M\left( {1\,;\, - 2} \right)\].
\[M\left( { - 2\,;\, - 4} \right)\].
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) có đồ thị như hình vẽ![Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) có đồ thị như hình vẽ Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) là A. \(1\). B. \( - 1\). C. \( - 2\). D. \(3\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/7-1759228777.png)
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) là
\(1\).
\( - 1\).
\( - 2\).
\(3\).
Giá trị nhỏ nhất của hàm số \[y = {x^2} - 2x + 3\] trên đoạn \(\left[ {2;4} \right]\) là
\(3.\)
\( - 1.\)
\(0.\)
\(1.\)
Đồ thị hàm số \[y = \frac{{1 + 2x}}{{x - 1}}\]có đường tiệm cận ngang là
\(x = 1\).
\(y = 1\).
\(x = 2\).
\(y = 2\)
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\) là
\(y = x - 3\).
\(y = x + 1.\)
\(y = - 3x + 1.\)
\(x = - 3y + 1.\)
Tổng số đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt x + 1}}{{3x - 9\sqrt x + 6}}\) là
3.
4.
2.
1.
Phần 2: Trắc nghiệm đúng sai
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\)và hàm số \(y = f'\left( x \right)\)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
![Xét tính đúng hoặc sai của các mệnh đề sau: a) [Mức độ 1] Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/8-1759228942.png)
Xét tính đúng hoặc sai của các mệnh đề sau:
a) [Mức độ 1] Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
b) [Mức độ 1] Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
c) [Mức độ 2] \(f'\left( 2 \right) = 4\).
d) [Mức độ 3] Hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{2}{x^2} + x + 2024\) đồng biến trên khoảng \(\left( { - \frac{5}{2}; - \frac{3}{2}} \right)\).
Cho hàm số \(y = {x^3} - 3x + 1\). Xét tính đúng hoặc sai của các mệnh đề sau:
a) Điểm cực tiểu của hàm số là \(x = 1\).
b) Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right)\).
c) Giả sử hàm số đã cho có hai điểm cực trị là \({x_1};{x_2}\). Khi đó giá trị \({x_1} \cdot {x_2} = - 1\).
d) Gọi \(A,B\)lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số. Khi đó, diện tích tam giác \(ABC\)là \(12\) với \(C( - 1;2)\).
Cho hàm số \(y = \frac{{x + m}}{{x - 1}}\) (\(m\) là tham số thực). Chọn đúng hoặc sai?
a) Khi \(m = 2\)thì giá trị lớn nhất của hàm số trên đoạn \(\left[ {2;5} \right]\) là \(4.\)
b) Khi \(m = 2\)thì giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {2;5} \right]\) là \(\frac{7}{4}.\)
c) Khi \(m < - 1\)thì giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {2;4} \right]\)là \(y\left( 4 \right).\)
d) Khi \(\mathop {\min }\limits_{[2;4]} y = 3\) thì giá trị của tham số \(m\) là \(1 \le m < 3\).
Các mệnh đề sau đúng hay sai?
a) Đồ thị hàm số \(y = \frac{{x + 1}}{{2x - 7}}\) có 1 tiệm cận đứng và 1 tiệm cận ngang.
b) Đồ thị hàm số \(y = \frac{x}{{{x^2} + 4}}\) có 1 tiệm cận ngang.
c) Đồ thị hàm số \(y = \frac{{2{x^2} - 6x + 2}}{{x + 3}}\) có tất cả 3 đường tiệm cận.
d) Đồ thị hàm số \(y = \frac{{\sqrt {25 - {x^2}} }}{{{x^2}}}\) có hai đường tiệm cận ngang là \(y = 1\) và \(y = - 1.\)
Phần 3: Câu trả lời ngắn
Sau khi phát hiện một dịch bệnh, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày phát hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \[f\left( t \right) = - {t^3} + 45{t^2} + 600t\], \[t \in \mathbb{N},{\rm{ }}t \le 30\]. Nếu coi \(f\left( t \right)\) là hàm số xác định trên đoạn \(\left[ {0;30} \right]\) thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \(t\). Trong 30 ngày đầu tiên, có bao nhiêu ngày mà tốc độ truyền bệnh lớn hơn 1200?
Trong một trò chơi, mỗi đội chơi được phát một tấm bìa hình chữ nhật kích thước 21 cm, 29,5 cm. Nhiệm vụ của mỗi đội là cắt ở bốn góc của tấm bìa này bốn hình vuông bằng nhau, rồi gập tấm bìa lại và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật như hình vẽ.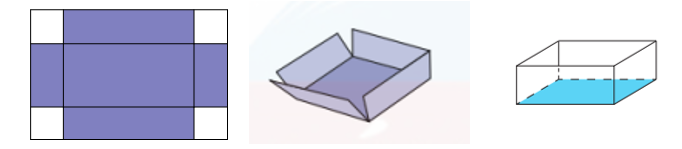 
Đội nào thiết kế được chiếc hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của hình vuông bị cắt để thu được hộp có thể tích lớn nhất. (Coi mép dán không đáng kể, kết quả làm tròn đến hàng phần trăm).
Điểm cực tiểu \[{x_{CT}}\] của hàm số \(y = {x^3} + 3{x^2} - 9x\)là:
Tìm \(m\) để hàm số \(y = {x^3} - 3m{x^2} + \left( {{m^2} + 2} \right)x - m + 1\) đạt cực đại tại \(x = 1\).
Cho hàm số \(y = \frac{{x - {m^2} - 1}}{{x - m}}\)có bao nhiêu giá trị nguyên m thỏa mãn \[\mathop {max}\limits_{\left[ {0;\,4} \right]} \,y = - 6\]
Biết tích các giá trị của tham số \(m\) để đồ thị của hàm số \(y = \frac{{2x - 4}}{{{x^2} + 2\left( {m - 2} \right)x + {m^2} + 1}}\) có đúng 2 đường tiệm cận là \(\frac{a}{b}\), \(\frac{a}{b}\) là phân số tối giản. Tính \(P = {a^2} + {b^2}\).
