Đề kiểm tra Bài tập cuối chương 1 (có lời giải) - Đề 2
21 câu hỏi
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = - {x^2} - 4\], \[\forall x \in \mathbb{R}\]. Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng \[\left( {2; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - 2;2} \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - \infty ; + \infty } \right)\].
Hàm số đồng biến trên khoảng \[\left( { - \infty ; - 2} \right)\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau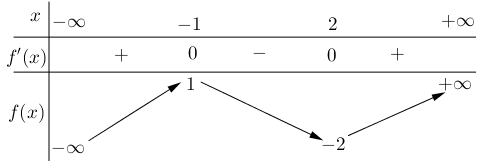
Giá trị cực tiểu của hàm số đã cho bằng
\( - 1\).
\(2\).
\( - 2\).
\(1\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau.![Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] trên \[\mathbb{R}\] bằng A. \(6\). B. \(9\). C. \( - 3\). D. \( - 1\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759222314.png)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] trên \[\mathbb{R}\] bằng
\(6\).
\(9\).
\( - 3\).
\( - 1\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số trên đoạn \(\left[ {0\,;\,3} \right]\) bằng A. \(4\). B. \(2\). C. \(3\). D. \(0\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/3-1759222372.png)
Giá trị lớn nhất của hàm số trên đoạn \(\left[ {0\,;\,3} \right]\) bằng
\(4\).
\(2\).
\(3\).
\(0\).
Đường tiệm cận ngang của đồ thi hàm số \(y = \frac{{2024x + 2025}}{{x - 5}}\) là
\(y = 2025\).
\(y = 2024\).
\(y = 1\).
\(y = - 5\).
Đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{15x - 6}}{{10x + 5}}\) là
\(x = \frac{3}{2}\).
\(x = - \frac{6}{5}\).
\(x = - \frac{1}{2}\).
\(x = \frac{2}{5}\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{ - {x^2} - 3x + 4}}{{x + 2}}\) là đường thẳng có phương trình?
\(y = - x - 1\).
\(y = x - 1\).
\(y = - x + 1\).
\(y = x + 1\).
Đường cong ở hình sau là đồ thị của hàm số nào?
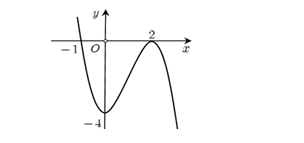
\[y = - {x^3} + 3{x^2} - 4.\]
\[y = {x^3} - 4.\]
\[y = {x^2} - 4.\]
\[y = - {x^2} - 4.\]
Hàm số nào sau đây có bảng biến thiên như hình?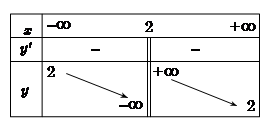
\[y = \frac{{2x + 1}}{{x - 2}}.\]
\[y = \frac{{2x - 5}}{{x - 2}}.\]
\[y = \frac{{2x + 1}}{{x + 2}}.\]
\[y = \frac{{2x - 1}}{{x + 2}}.\]
Đường cong dưới đây là đồ thị của hàm số nào?
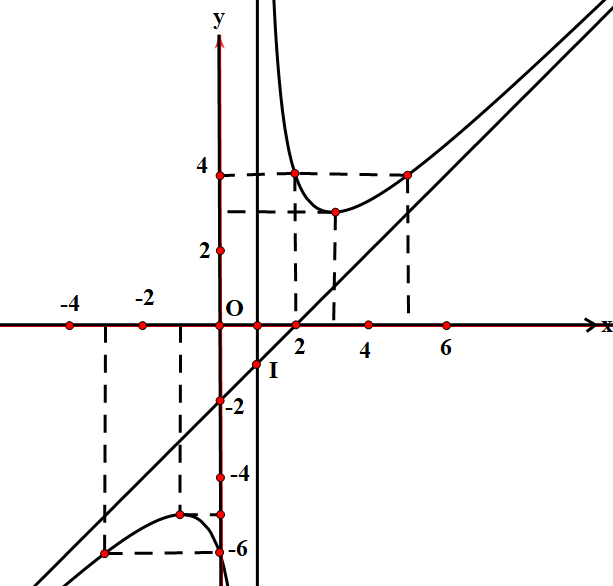
\(y = - {x^3} + {x^2} - 2x + 1\).
\(y = \frac{{{x^2} - x + 3}}{{x - 1}}\).
\(y = \frac{{{x^2} - 3x + 6}}{{x - 1}}\).
\(y = \frac{{2x + 3}}{{x - 1}}\).
Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã nhận thấy rằng: nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng là \(P\left( n \right) = 800 - 20n\,\,\left( g \right)\). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
\(19\).
\(20\).
\(21\).
\(22\).
Hàm số ![Hàm số đạt cực đại tại điểm A. \[x = - 1\]. B. \[x = 1\]. C. \[x = 3\]. D. \(x = - 3\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/7-1759222811.png){kind=small}
đạt cực đại tại điểm
\[x = - 1\].
\[x = 1\].
\[x = 3\].
\(x = - 3\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
[NB-TH-TH-TH] Xét tính đúng sai của các mệnh đề sau:
a) Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên như sau:
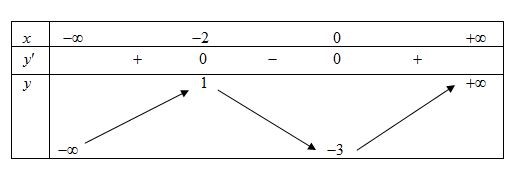
Khi đó hàm số trên nghịch biến trên khoảng \[\left( { - 2\,;\;0} \right)\].
b) Hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\) đồng biến trên \[\left( {2\,;\; + \infty } \right)\].
c) Cho hàm số \(y = f\left( x \right)\) có \(f'\left( x \right) = {x^{2017}}{\left( {x - 1} \right)^{2018}}\left( {x + 1} \right)\,\,\forall x \in \mathbb{R}\). Khi đó hàm số đã cho có 3 điểm cực trị.
d) Đồ thị hàm số\(y = {x^3} - 3{x^2} + 2ax + b\) có điểm cực tiểu\(A(2; - 2)\). Khi đó \(a + b = 2\).
Xét tính đúng sai của các mệnh đề sau:
a) Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên như sau:
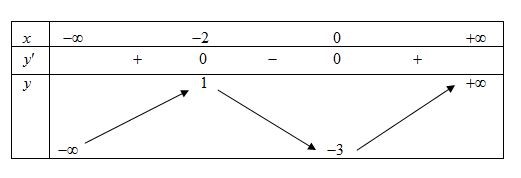
Khi đó giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\)trên \[\left( { - 2;\; + \infty } \right)\] bằng -3.
b) Giá trị lớn nhất của hàm số \(y = {x^3} - 2{x^2} - 7x + 1\) trên đoạn \(\left[ { - 2;1} \right]\) bằng -1.
c) Giá trị lớn nhất của hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\) trên \[\left[ {2;3} \right]\] bằng 3.
d) Một hãng dược phẩm cần một số lọ đựng thuốc dạng hình trụ với dung tích \(16\pi c{m^3}\). Để ít tốn nguyên liệu sản xuất nhất thì bán kính đáy\(R\)của lọ bằng \(2cm\).
Các mệnh đề sau là đúng hay sai?
a) Đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 3}}{{x + 2}}\) là \(y = 2\).
b) Đồ thị hàm số \(y = g\left( x \right) = \frac{{{x^2} - 1}}{{{x^2} + 5x + 4}}\) có hai tiệm cận đứng.
c) Đồ thị hàm số \(y = h\left( x \right) = \sqrt {{x^2} - 2x + 2} \) không có tiệm cận xiên.
d) Một bình chứa 500(gam) dung dịch nước muối có nồng độ 30%. Người ta rót thêm vào bình một dung dịch nước muối có nồng độ 45% với tốc độ 0,5 (gam/giây). Khi thời gian rót rất lâu thì nồng độ của dung dịch muối sẽ càng gần với nồng độ của dung dịch ban đầu.
Các mệnh đề sau là đúng hay sai?
a) Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ:
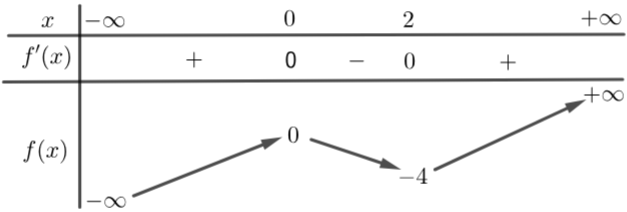
Hàm số đã cho nghịch biến trên khoảng \(\left( { - 4;0} \right)\).
b) Hàm số \(y = f\left( x \right) = \frac{{x - 1}}{{x + 1}}\) đồng biến trên \(\left( { - \infty \,;\, + \infty } \right)\).
c) Hàm số \(y = g\left( x \right) = \frac{{{x^2} - 1}}{x}\) không có cực trị.
d) Một doanh nghiệp mua một chiếc máy giá 5000 (USD) để sản xuất \(x\left( {kg} \right)\) sản phẩm loại A. Trong thực tế, mỗi kg sản phẩm được sản xuất ra cần phải có nguyên liệu với giá 4 (USD). Khi doanh nghiệp này sản xuất một số lượng rất lớn sản phẩm thì chi phí để sản xuất được mỗi kg sản phẩm giảm dần và đạt giá trị nhỏ nhất là 4,1 (USD).
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \left( {m - 1} \right){x^3} - \left( {m - 1} \right){x^2} + 3x + 2024\) đồng biến trên tập xác định?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thoả mãn \(f'\left( x \right) = x{\left( {x - 1} \right)^2}{\left( {x - 2} \right)^3}\). Hàm số \(g\left( x \right) = f\left( {{x^2} - 2x + 2} \right)\) có bao nhiêu điểm cực trị?
Tìm \(m\) để giá trị lớn nhất của hàm số \(y = \frac{{x - m}}{{x + 1}}\) trên đoạn \(\left[ {1;3} \right]\) bằng \(2\).
Chị Hà dự định sử dụng hết \(4\,{{\rm{m}}^2}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu mét khối (kết quả làm tròn đến hàng phần trăm)?
Có bao nhiêu giá trị thực của tham số \[m\] để đồ thị hàm số \[y = \frac{{{x^2} - 1}}{{{x^2} + \left( {2 - m} \right)x + 2m + 1}}\] có đúng hai đường tiệm cận?
