25 câu trắc nghiệm Toán 12 Kết nối tri thức Bài tập cuối chương 1 (Đúng sai - Trả lời ngắn) có đáp án
40 câu hỏi
Bài tập cuối chương I
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số y = f(x) có bảng biến thiên như sau:
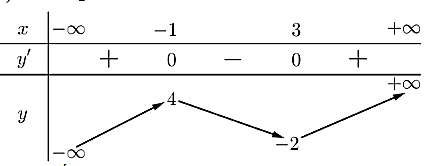
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
(−2; 4).
(−2; +∞).
(−1; 3).
(−∞; −1).
Cho hàm số y = f(x) liên tục trên ℝ, có đạo hàm f'(x) = (2x + 1)(x – 3)2(x – 2)3 với mọi x Î ℝ. Số điểm cực đại của hàm số y = f(x) là
0.
1.
2.
3.
Giá trị nhỏ nhất của hàm số f(x) = x3 – 3x + 2 trên đoạn [−3; 3] bằng
−16.
20.
0.
4.
Tiệm cận đứng của đồ thị hàm số 
là
A. 
.
y = 4
x = 4.
x = 1.
Cho hàm số y = f(x) có đồ thị là đường cong như hình bên dưới
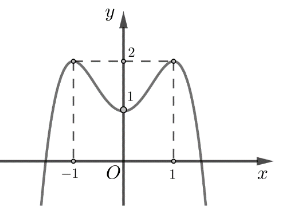
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(0; 1).
(−∞; 0).
(1; +∞).
(−1; 0).
Cho hàm số f(x) liên tục trên đoạn [−2; 3] có đồ thị như hình vẽ dưới đây
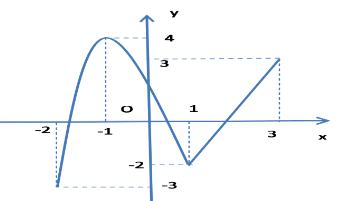
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [−2; 3]. Giá trị của 2m – 3M bằng
−13.
−18.
−16.
−15.
Cho hàm số f(x) liên tục trên ℝ\{1} và có bảng biến thiên như sau
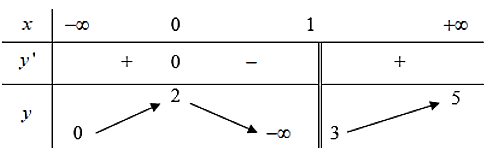
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
4.
1.
3.
2.
Đồ thị sau là đồ thị của hàm số nào?
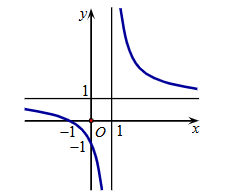
A. 
.
B. 
.
C. 
.
D. 
.
Đồ thị như hình bên dưới là đồ thị của hàm số nào?
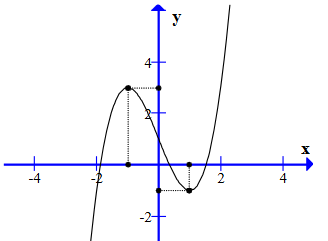
y = −x3 + 3x2 + 1.
y = x3 – 3x – 1.
y = x3 – 3x + 1.
y = −x3 – 3x2 – 1.
Tiệm cận xiên của đồ thị hàm số 
là
y = −2.
y = 1.
y = x + 2.
y = x.
Cho hàm số 
có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?
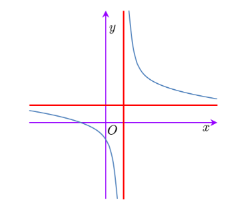
ac > 0, bd > 0.
ab < 0, cd < 0.
ac > 0, cd < 0.
bd < 0, ad > 0.
Cho hàm số y = f(x) liên tục và có đạo hàm trên ℝ. Hàm số f'(x) có đồ thị như hình bên
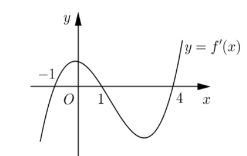
Hàm số y = f(x) đồng biến trên khoảng
(−1; 1).
(−1; 2024).
(−∞; −1).
(1; +∞).
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên như hình
Mệnh đề nào sau đây sai?
Hàm số có hai cực trị.
Phương trình y' = 0 có 2 nghiệm.
Phương trình y = 0 có 2 nghiệm dương và 1 nghiệm âm.
Giá trị cực đại của hàm số là 3.
Cho hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như sau:
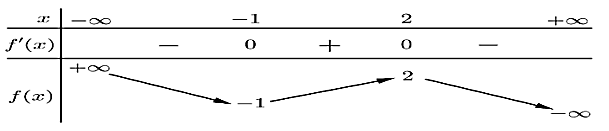
Số đường tiệm cận của đồ thị hàm số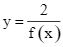 
là
5.
4.
3.
2.
Cho hàm số f(x) có đạo hàm là f'(x) =3x2 + ex. Giá trị lớn nhất của hàm số f(x) trên [0; 2] là:
f(2).
f(0).
f(1).
12 + e2.
a) Đồ thị (C) có tiệm cận xiên là y = −x – 6
b) Đồ thị (C) nhận điểm I(3; −9) làm tâm đối xứng
c) Hàm số y = f(x) đồng biến trên khoảng (3; 7)
d) Đồ thị (C) có hai điểm cực trị nằm về hai phía đối với Oy.
a) Hàm số y = f(x) có hai cực trị
b) Hàm số y = f(x) giảm trên (1; +∞).
c) Giá trị nhỏ nhất của hàm số y = f(x) trên [−3; 0] là f(−3)
d) Giá trị lớn nhất của hàm số y = 0,2f(x) trên [0; 2] là ef(1).
a) Hàm số f(x) đồng biến trên khoảng (−2; 2)
b) Giá trị cực tiểu của hàm số là −1
c) Số nghiệm thực của phương trình 
là 3.
d) Phương trình f(x3 + 3x2 – 1) = 1 có đúng 7 nghiệm thực phân biệt.
a) Chiều cao của bể nước là 
(m).
b) Diện tích các mặt cần xây là 
(m2).
c) Chi phí vật liệu thấp nhất khi x = 2 (m).
d) Diện tích các mặt cần xây đạt giá trị nhỏ nhất là 75 (m2)
a) Điểm cực tiểu của hàm số f(x) là x = −1
b) Giá trị nhỏ nhất của hàm số f(x) trên đoạn [1; +∞) là −1.
c) Phương trình f(x) = 0 có 3 nghiệm phân biệt.
d) Hàm số h(x) = f(2 – 3x) đồng biến trên khoảng 
.
PHẦN III. TRẢ LỜI NGẮN
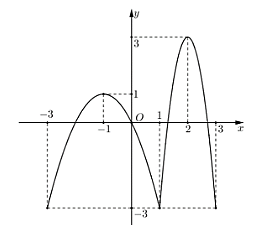
Cho hàm số y = f'(x) có đồ thị như hình vẽ bên dưới. Giá trị lớn nhất của hàm số y = f(x) trên đoạn [−1; 1] là f(x0). Tìm x0.
Cho hàm số y = f(x) có f'(x) = (3x2 – 10x + 3)(3x2 – 25x + 48). Giả sử hàm số y = f(x) nghịch biến trên khoảng (a; b). Trong khoảng (a; b) có nhiều nhất bao nhiêu giá trị nguyên nhỏ hơn 2024.
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2 – 1)(x – 4) với mọi x ∈ ℝ. Hàm số g(x) = f(3 – x) có bao nhiêu điểm cực đại?
Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức 
(f(t) được tính bằng nghìn người) (Nguồn : Giải tích 12 nâng cao, NXBGD Việt Nam, 2020). Xem y = f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Đồ thị hàm số y = f(t) có đường tiệm cận ngang là y = a. Giá trị của a là bao nhiêu ?
Cho hàm số 
có đồ thị như hình vẽ
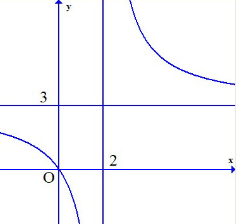
Tính giá trị của P = 2024a – 25b.
