Đề kiểm tra Bài tập cuối chương 1 (có lời giải) - Đề 3
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x - 2} \right)^3}\), với mọi \(x \in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {1;\,\,3} \right)\).
\(\left( { - 1;\,\,0} \right)\).
\(\left( {0;\,\,1} \right)\).
\(\left( { - 2;\,\,0} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {1\,;\, + \infty } \right)\).
\(\left( { - \infty \,;\,1} \right)\).
\(\left( { - 1\,;\, + \infty } \right)\).
\(\left( { - \infty \,;\, - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2\,;\,2} \right]\) và có đồ thị như hình vẽ bên dưới.![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2\,;\,2} \right]\) và có đồ thị như hình vẽ bên dưới. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759223532.png)
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 2\,;\,2} \right]\). Giá trị của \(M + m\) bằng
\[0\].
\[1\].
\[4\].
\[3\].
Cho hàm số\(y = f(x)\)có bảng biến thiên như sau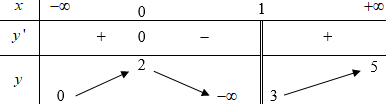
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
\(4\).
\(3\).
\(2\).
\(1\).
Cho hàm số\(y = \frac{{2x + 1}}{{x - 3}}\). Ttiệm cận ngang của đồ thị hàm số đã cho là
\(x = 3\).
\(x = 2\).
\(x = - \frac{1}{2}\).
\(y = 2\).
Biết hàm số \(y = \frac{{x + a}}{{x - 1}}\) (\(a\) là số thực cho trước, \(a \ne - 1\)) có đồ thị như trong hình vẽ sau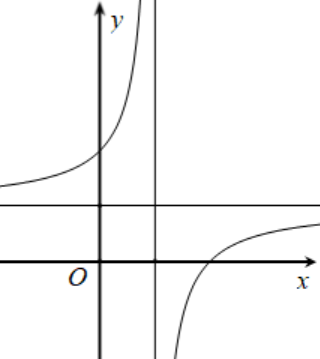
Mệnh đề nào dưới đây đúng?
\(y' > 0,\,\forall x \ne 1\).
\(y' > 0,\,\forall x \in \mathbb{R}\).
\(y' < 0,\,\forall x \in \mathbb{R}\).
\(y' < 0,\,\forall x \ne 1\).
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?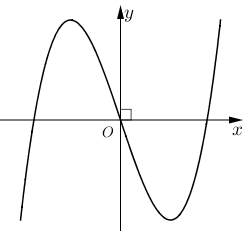
\(y = {x^3} - 3x\).
\(y = - {x^3} + 3x\).
\(y = {x^4} - 2{x^2}\).
\(y = - {x^4} + 2{x^2}\).
Tập hợp tất cả các giá trị của tham số \[m\] để hàm số \[y = {x^3} + \left( {m + 1} \right){x^2} + 3x + 2\] đồng biến trên \[\mathbb{R}\] là
\[\left[ { - 4;2} \right]\].
\[\left( { - 4;2} \right)\].
\[\left( { - \infty ; - 4} \right] \cup \left[ {2; + \infty } \right)\].
\[\left( { - \infty ; - 4} \right) \cup \left( {2; + \infty } \right)\].
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 2}}\)trên đoạn \(\left[ {3;7} \right]\). Tính giá trị của \({M^2} + m\).
\[52\].
\[58\].
\[16\].
\[10\].
Đồ thị hàm số \[y = \frac{{{x^2} - 3x - 4}}{{{x^2} - 16}}\] có bao nhiêu đường tiệm cận đứng ?
\(1\).
\(0\).
\(2\).
\(3\).
Đồ thị của hàm số \(y = {x^3} - 3x + 2\) cắt trục tung tại điểm có tung độ bằng
\(0\).
\(1\).
\(2\).
\( - 2\).
Số giao điểm của đồ thị hàm số \(y = {x^3} - 3x + 1\) và trục hoành là
\(3\).
\(0\).
\(2\).
\(1\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\)và có đồ thị như hình vẽ :
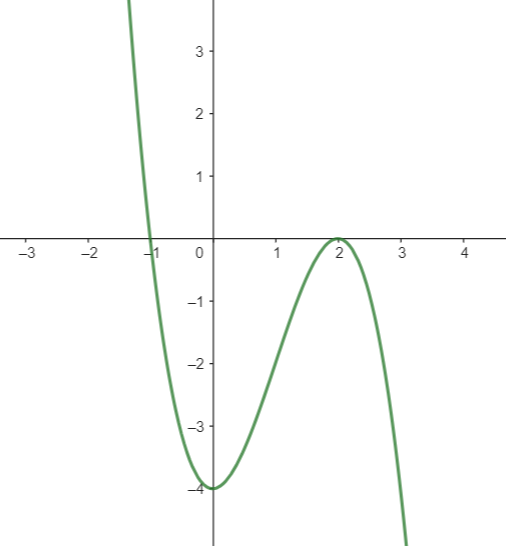
Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
b) Hàm số đạt cực đại tại \(x = 0\).
c) Giá trị nhỏ nhất của hàm số trên \(\left[ { - 1;1} \right]\) bằng \( - 4\).
d) Hàm số \(g\left( x \right) = f\left( {3 - x} \right)\) nghịch biến trên \(\left( {2;5} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm \[f'\left( x \right)\] như hình bên dưới.
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm \[f'\left( x \right)\] như hình bên dưới. Xét tính đúng sau của các mệnh đề sau: a. Hàm số đã cho đồng biến trên các khoảng \(\ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/11-1759224009.png)
Xét tính đúng sau của các mệnh đề sau:
a. Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0;1} \right)\).
b. Hàm số đã cho nghịch biến trên khoảng \(\left( {3; + \infty } \right)\).
c. Hàm số đã cho có \(2\) điểm cực trị.
d. Hàm số đã cho đạt cực tiểu tại điểm \[x = 0\].
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \(y = f\left( x \right) = \frac{{3x - 1}}{{x - 3}}\) trên đoạn\(\left[ {0;\;2} \right]\). Xét tính đúng sai của các mệnh đề sau:
a. Hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\)
b. \(M = \mathop {{\rm{max}}y}\limits_{\left[ {0;\;2} \right]} = f\left( 1 \right) = \frac{1}{3}\)
c. \(m = \mathop {{\rm{min}}y}\limits_{\left[ {0;\;2} \right]} = f\left( 2 \right) = - 5\)
d. \(P = M.m = - \frac{5}{3}.\)
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), có bảng biến thiên như sau:
![Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), có bảng biến thiên như sau: Xét tính đúng sai của các mệnh đề sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3635-1759224168.png)
Xét tính đúng sai của các mệnh đề sau:
a. Đồ thị hàm số có tiệm cận đứng \[y = - 1\] và tiệm cận ngang \[x = - 2.\]
b. Đồ thị hàm số có duy nhất một tiệm cận.
c. Đồ thị hàm số có ba tiệm cận.
d. Đồ thị hàm số có tiệm cận đứng \[x = - 1\] và tiệm cận ngang \[y = - 2.\]
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Cho hàm số \(y = \frac{{2{x^2} + 5x + 4}}{{x + 2}}\). Độ dài của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số bằng.
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên dưới. Số điểm cực trị của hàm số đã cho là
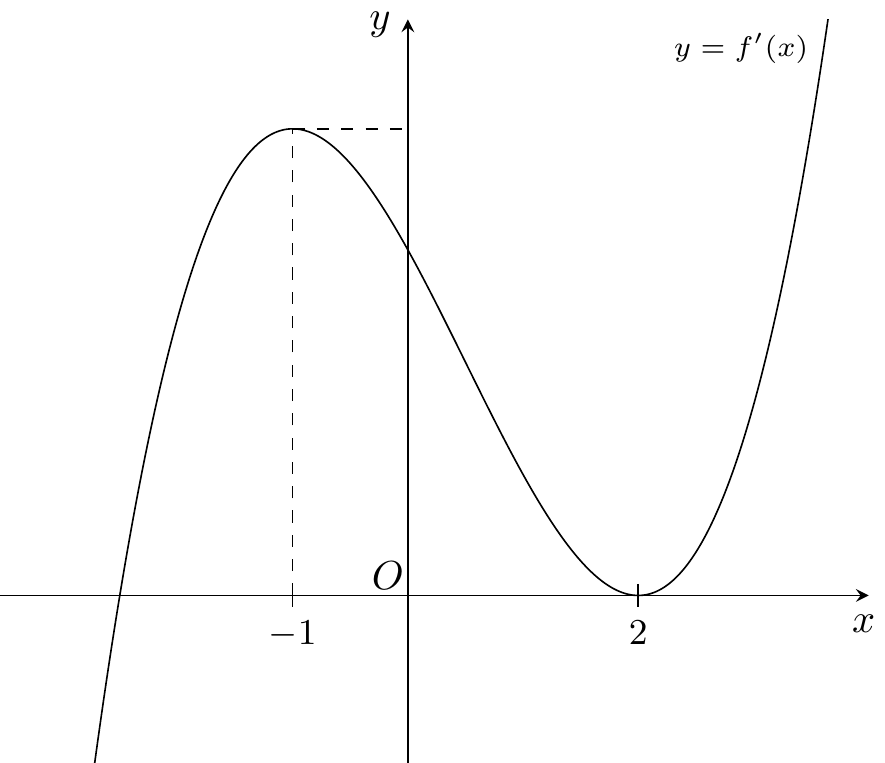
Tiệm cận xiên của đồ thị hàm số \[y = f\left( x \right) = \frac{{{x^2} - x + 1}}{{x - 1}}\] có dạng \(y = ax + b\,,\,\,\,\left( {a,b \in \mathbb{Z}} \right)\). Tính giá trị biểu thức \(P = 5a + 2024b\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và bảnng xét dấu đạo hàm như hình vẽ sau: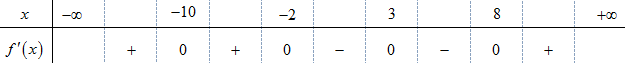
Tìm \(m\) để hàm số \(y = f\left( {{x^3} + 4x + m} \right)\) nghịch biến trên khoảng \(\left( { - 1;1} \right)\)?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{\left( {x - m - 1} \right)^2} + 2019\), với \(m\) là tham số thực. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {5;{\kern 1pt} {\kern 1pt} 6} \right)\). Tính tổng tất cả các phần tử trong \(S\) bằng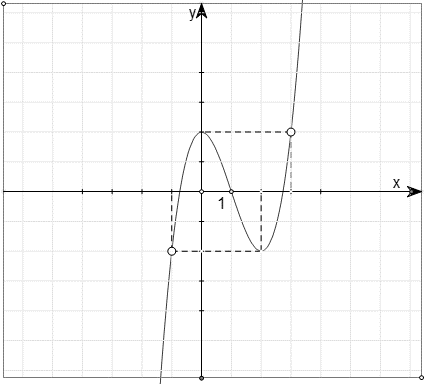
Một hộp sữa dung tích \[1\] lít có dạng hình hộp chữ nhật với đáy là hình vuông cạnh bằng \[x\,\,\left( {cm} \right)\] và chiều cao \[h\,\,\left( {cm} \right)\]. Tìm giá trị của \[x\] để diện tích toàn phần của hình hộp là nhỏ nhất.