Đề kiểm tra Bài tập cuối chương 1 (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Các khoảng đồng biến của hàm số \(y = {x^3} - 3{x^2} + 2\) là:
\(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
\(\left( {3; + \infty } \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( {2; + \infty } \right)\).
Cho hàm số \[y = 27{x^3} + 108{x^2} - 81x + 189\]. Điểm cực tiểu của hàm số là.
\( - 3\).
\[\frac{1}{3}\].
175.
675.
Giá trị lớn nhất của hàm số\[f\left( x \right) = {x^3} - 8{x^2} + 16x - 9\] trên đoạn \(\left[ {1;3} \right]\) là
\[\mathop {\max }\limits_{\left[ {1;{\rm{ }}3} \right]} f(x) = 0.\]
\[\mathop {\max }\limits_{\left[ {1;{\rm{ }}3} \right]} f(x) = \frac{{13}}{{27}}{\rm{.}}\]
\[\mathop {\max }\limits_{\left[ {1;{\rm{ 3}}} \right]} f(x) = - 6.\]
\[\mathop {\max }\limits_{\left[ {1;{\rm{ 3}}} \right]} f(x) = 5.\]
Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^4} - 4{x^2} + 1\) trên đoạn \(\left[ {1\;;\;3} \right]\)bằng
\(46\).
\(64\).
\(3\).
\(\sqrt 2 \).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) là
\(y = 1\).
\(y = 2\).
\(x = 1\).
\(x = 2\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 1}}\)là
\[x = 1\].
\[y = 2\].
\[x = 2\].
\[x = - 1\].
Đường thẳng nào sau đây là tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x + 1}}{{x + 2}}\).
\(y = 2x\).
\(y = 2\).
\(y = 2x - 7\).
\(x = - 2\).
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau: 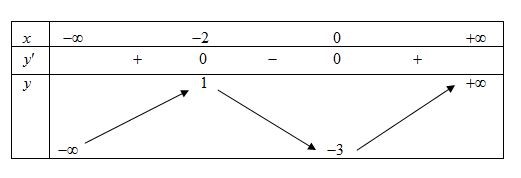 Hàm số
Hàm số ![]() nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho bảng biến thiên như hình vẽ dưới. Hỏi đây là bảng biến thiên của hàm số nào trong các hàm số sau? 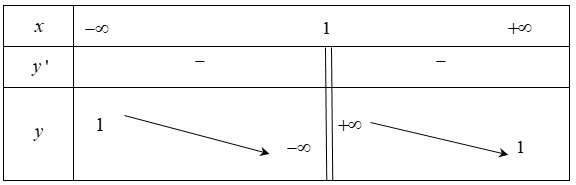
\(y = \frac{{x - 3}}{{x - 1}}\).
\(y = \frac{{ - x + 2}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x + 1}}\).
\(y = \frac{{x + 2}}{{x - 1}}\).
Cho hàm số \[y = \frac{{{x^2} - 2x}}{{1 - x}}\]. Khẳng định nào sau đây đúng?
Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Cho chuyển động được xác định bởi phương trình \[s = 3{t^3} + 4{t^2} - t\], trong đó \(t\) được tính bằng giây và \(s\) được tính bằng mét. Vận tốc của chuyển động khi \[t = 4s\] bằng
\[175m/s.\]
\[41m/s.\]
\[176m/s.\]
\[20m/s.\]
Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = {x^2}(x - 1)\) với mọi số thực \(x\). Số điểm cực tiểu của hàm số \(f\left( x \right)\) là
0.
1.
2.
3.
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Cho các hàm số sau \(f\left( x \right) = {x^3} - 3{x^2} + 2025\), \(g\left( x \right) = \frac{{{x^2} - 2x + 1}}{{x - 2}}\).
Trong các mệnh đề sau, đâu là mệnh đề đúng đâu là mệnh đề sai?
a) Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \[\left( {0;2} \right)\].
b) Hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( {1;3} \right)\).
c) Điểm cực đại của hàm số \(f\left( x \right)\) là \(x = 0\)
d) Đồ thị hàm số \(g\left( x \right)\) có đường thẳng đi qua hai điểm cực trị \[AB\] cũng đi qua điểm \(N(2;2)\).
Cho các hàm số sau \(f(x) = {x^3} - 8{x^2} + 16x - 9\), \(h\left( x \right) = \frac{{{x^2} - x + 1}}{{x - 1}}\).
Trong các mệnh đề sau, đâu là mệnh đề đúng đâu là mệnh đề sai?
a) Giá trị lớn nhất của hàm số \[f\left( x \right)\] trên đoạn \([ - 1;1]\) là \(0\).
b) Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x)\) trên đoạn \[\left[ {1;3} \right]\] lần lượt là a, b. Khi đó giá trị của \(27a - b\) bằng \(13\).
c) Giá trị nhỏ nhất của hàm số \(h\left( x \right)\) trên khoảng \((1; + \infty )\) là \(3\)
d) Độ giảm huyết áp của một bệnh nhân sau khi sử dụng thuốc được đo bởi công thức \(G(x) = 0,025{x^2}(30 - x)\) trong đó \(x({\rm{mg}})\) và \(x > 0\) là liều lượng thuốc tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng \(20mg\)
a) Đồ thị hàm số \(y = \frac{{x - 2}}{{x + 3}}\) có đường tiệm cận ngang là đường thẳng \(y = 1\).
b) Đồ thị hàm số \(y = \frac{{{x^2} - 3x}}{{x + 1}}\) có đường tiệm cận đứng là đường thẳng \(x = - 1\).
c) Đồ thị hàm số \(y = \frac{{{x^2} - 3x + 2}}{{x + 3}}\) có đường tiệm cận xiên là đường thẳng \(y = x - 6\).
d) Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất \(x\) (sản phẩm) là \(C\left( x \right) = 5x + 15\) (triệu đồng). Khi đó, \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình của mỗi sản phẩm. Tiệm cận ngang của đồ thị hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là đường thẳng \(y = 5\).
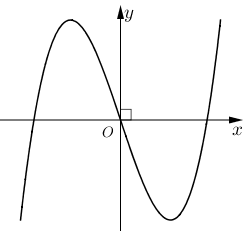
a) Đồ thị của hàm số \(y = {x^3} - 3x + 1\) có dạng như đường cong trong hình bên.
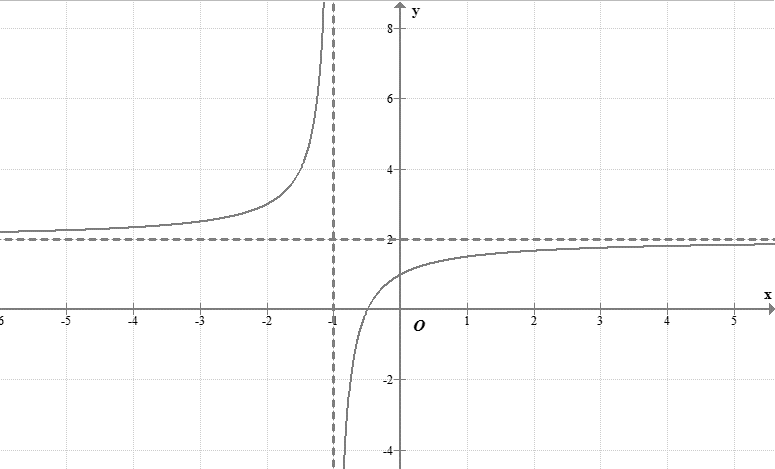
b) Đồ thị của hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) có dạng như đường cong trong hình bên.
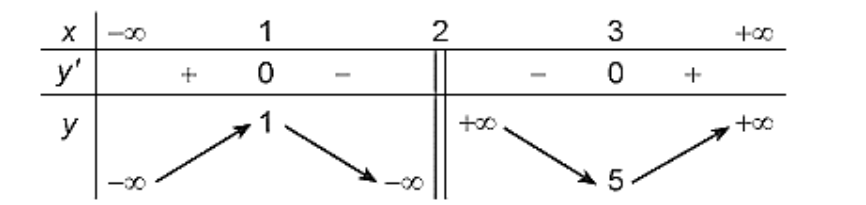
c) Hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\) có bảng biến thiên như sau
d) Giả sử số lượng tế bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số \(P\left( t \right) = \frac{a}{{b + {e^{ - 0,75t}}}}\) trong đó thời gian \[t\] được tính bằng giờ, các hằng số \(a,\,b \in \mathbb{R}\), đồng thời đạo hàm \[P'\left( t \right)\] biểu thị tốc độ gia tăng tế bào. Tại thời điểm ban đầu \(t = 0\), quần thể có \(20\) tế bào và tăng với tốc độ \(10\) tế bào/giờ. Khi đó \(a = 25\) và \(b = \frac{1}{2}\).
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Cho hàm số \[y = f\left( x \right)\] có đạo hàm trên \[\mathbb{R}\], thỏa mãn \[f\left( { - 1} \right) = f\left( 3 \right) = 0\] và đồ thị của hàm số \[y = f'\left( x \right)\] có dạng như hình dưới đây.Hàm số \[y = {\left( {f\left( x \right)} \right)^2}\]có bao nhiêu khỏang nghịch biến.![Cho hàm số \[y = f\left( x \right)\] có đạo hàm trên \[\mathbb{R}\], thỏa mãn \[f\left( { - 1} \right) = f\left( 3 \right) = 0\] và đồ thị của hàm số \[y = (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/11-1759228136.png)
Đồ thị hàm số \(y = {x^3} - 3{x^2} - 9x + 5\) có điểm cực đại và điểm cực tiểu lần lượt là \(A\) và \(B\) .
Gọi \(I\) là giao điểm của \(AB\) với trục \(Ox\). Khi đó tỷ số \(\frac{{IA}}{{IB}} = \frac{b}{c}\), tính \(T = b + c\).
Gọi \(M\,,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{3\sin x + 2}}{{\sin x + 1}}\) trên đoạn \(\left[ {0\,;\,\frac{\pi }{2}} \right]\). Khi đó giá trị của \({M^2} + {m^2} = \frac{b}{c}\) , tính \(T = b - c\)
Vận tốc của một tàu con thoi từ lúc cất cánh tại thời điểm \[t = 0\,\,\left( s \right)\] cho đến thời điểm \[t = 126\,\,\left( s \right)\] được cho bởi công thức \[v(t) = 0,001302{t^3} - 0,09029{t^2} + 83\] (vận tốc được tính bằng đơn vị \[ft/s\]). Hỏi tàu con thoi đạt vận tốc lớn nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm).
Một mảnh vườn hình chữ nhật có diện tích bằng \(900\;\,{m^2}\). Biết chiều dài của mảnh vườn là \(x\,\,\left( m \right)\).Gọi biểu thức tính chu vi của mảnh vườn là \(P\left( x \right)\) (mét). Biết rằng phương trình tiệm cận xiên của đồ thị hàm số \(P\left( x \right)\) là \[y = ax + b\]. Tính giá trị biểu thức \[T = {10^a} + b\]
Biết rằng đồ thị hàm số \[y = \frac{{x + 1}}{{x - 1}}\] cắt đường thẳng \[y = 2x - 1\] tại hai điểm phân biệt \[A,\,\,B\]. Tính diện tích tam giác \[OAB\].