Đề cương ôn tập giữa kì 1 Toán 8 Kết nối tri thức cấu trúc mới (Tự luận) có đáp án - Phần 2

Một người làm vườn có hai khu vườn, khu vườn hình chữ nhật có chiều dài \(\left( {x + 2} \right)\,\,{\rm{m}}\,{\rm{,}}\)chiều rộng \(\left( {x - 1} \right)\,\,{\rm{m}}\,{\rm{,}}\) khu vườn hình vuông cạnh là \(\left( {x + 1} \right)\,\,{\rm{m}}\,{\rm{.}}\) Viết biểu thức đại số tính tổng diện tích của hai khu vườn trên.

Thầy Việt dự định mua \[x\] quyển vở để trao thưởng cho những học sinh tiến bộ cuối năm học, mỗi quyển vở giá \[y\] đồng. Nhưng khi đến cửa hàng thầy Việt thấy giá vở đã giảm 2000 đồng mỗi quyển nên quyết định mua thêm 30 quyển.

a) Tìm đa thức biểu thị số tiền thầy Việt phải trả cho cửa hàng.

b) Hãy cho biết bậc của đa thức vừa tìm được ở câu a và tính số tiền thầy Việt phải trả nếu thầy mua 50 quyển vở và giá 1 quyển vở khi chưa giảm là 7000 đồng.

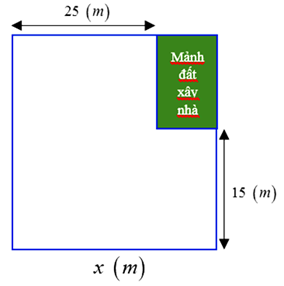Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\,,\) đường cao \(AH\,.\) Từ \(H\) kẻ \(HM \bot AB\,\,\left( {M \in AB} \right)\,.\)Kẻ \(HN \bot AC\,\,\left( {N \in AC} \right)\,.\)

a) Chứng minh tứ giác \[AMHN\] là hình chữ nhật .

b) Trên tia đối của tia \[MH\] lấy điểm \[P\] sao cho \[M\] là trung điểm của \[PH.\] Chứng minh tứ giác \(APMN\)là hình bình hành.

c) Gọi \(I\) là trung điểm của \(HC\,,\) lấy \(K\) trên tia \(AI\) sao cho \(I\) là trung điểm của \(AK\,.\)Chứng minh \(MNCK\) là hình thang cân.

d) \(MN\) cắt \(AH\) tại \(O,\)\(CO\) cắt \(AK\) tại \(D\,.\)Chứng minh \(AK = 3AD\,.\)

Cho tam giác nhọn\[ABC\]có \[AB < BC.\] Từ trung điểm \(M\) của cạnh \(AB\) kẻ đường thẳng song song với \(BC\) cắt cạnh \(AC\) tại \(N.\) Trên cạnh \(BC\) lấy điểm \(D\) sao cho \(BD = MN.\) Kẻ đường cao \[AH\left( {H \in BC} \right)\] của tam giác \[ABC\]. Chứng minh:

a) Tứ giác \(BMND\) là hình bình hành.

b) Tam giác \(AMH\) cân.

 b) Tứ giác \(DHMN\) là hình thang cân.

Cho hình bình hành \[ABCD\] có cạnh \(AB = 2AD.\) Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[AB\] và \[CD.\]

a) Chứng minh rằng \(DMBN\) là hình bình hành.

b) Chứng minh rằng \(AN\) là tia phân giác của góc \[DAB.\]

c) Gọi giao điểm của \(AN\) với \[DM\]là \[P,{\rm{ }}CM\] với \[BN\] là \[Q.\] Tìm điều kiện của hình bình hành\[ABCD\] để tứ giác \[PMQN\] là hình vuông.

Xét hai hình bình hành \[MNBA\] và \[MNCB.\]

a) Chứng minh \[B\] là trung điểm của \[AC.\]

b) Hỏi tam giác \[MAB\] thoả mãn điều kiện gì để \[MNCA\] là một hình thang cân?

c) Lấy điểm \[D\] để tứ giác \[MNDC\] là hình bình hành. Hỏi tam giác \[MAB\] thoả mãn điều kiện gì để \[MNDA\] là một hình thang cân?

Cho hình bình hành \[ABCD\]. Trên cạnh \[AB\] lấy điểm \[M,\] trên cạnh \[DC\] lấy điểm \[N\] sao cho \[AM = CN.\]

a) Chứng minh \[AN\,{\rm{//}}\,CM.\]

b) Gọi \[O\] là giao điểm của \[AC\] và \[BD.\] Chứng minh \[O\] là trung điểm của \[MN.\]

Chứng minh đẳng thức sau:

\(\left( {x + y} \right)\left( {{x^4} - {x^3}y + {x^2}{y^2} - x{y^3} + {y^4}} \right) = {x^5} + {y^5}\).

Cho các số \(x,y\) thỏa mãn đẳng thức: \(5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0.\) Tính giá trị của biểu thức \(M = {\left( {x + y} \right)^{2023}} + {\left( {x - 2} \right)^{2024}} + {\left( {y + 1} \right)^{2025}}\).

Tính giá trị của biểu thức: \(A = 4\left( {{3^2} + 1} \right)\left( {{3^4} + 1} \right)\left( {{3^8} + 1} \right)\,\,...\,\,\left( {{3^{64}} + 1} \right)\).

Chứng minh rằng nếu \[{a^4} + {b^4} + {c^4} + {d^4} = 4abcd\] và\(a,\,\,b,\,\,c,\,\,d\) là các số dương thì \[a = b = c = d.\]

Tìm \(m,\,\,n \in \mathbb{N}\) để phép chia sau đây là phép chia hết:

\(\left( {4{x^6}{y^7} - 10{x^5}{y^6} + 8{x^4}{y^5}} \right):\left( { - 4{x^m}{y^n}} \right)\).

Cho các số x, y thoả mãn \({x^2} + {y^2} - 3x - 3y + xy + 3 = 0\). Tính giá trị của biểu thức \(Q = {\left( {x - y} \right)^{2023}} + {\left( {x - 2} \right)^{2024}} + {y^{2025}}\).

Tìm giá trị nhỏ nhất củabiểu thức \[M = 9{x^2} + 6{y^2} + 18x - 12xy - 12y - 27\].

Cho các số thực \(a,\,\,b,\,\,c\) thoả mãn \({a^2} + {b^2} + {c^2} = 3\) và \(a + b + c + ab + bc + ca = 6.\) Tính giá trị của biểu thức \[A = \frac{{{a^9} + {b^{11}} + {c^{2025}}}}{{{a^{2023}} + {b^{2024}} + {c^{2025}}}}.\]

Ao Bà Om, hay Ao Vuông là một thắng cảnh độc đáo và nổi tiếng ở tỉnh Trà Vinh, Việt Nam. Mặt ao nước trong xanh và phẳng lặng được phủ bởi hoa sen, hoa súng. Ao được bao bọc xung quanh bởi các gò cát mấp mô với các hàng cây sao, cây dầu cổ thụ hàng trăm năm tuổi có rễ nổi lên khỏi mặt đất tạo nên những hình thù kì lạ. Ao có hình chữ nhật, rộng \[x\] mét, dài \(\left( {x + 200} \right)\) mét, được đào ở trung tâm miếng đất hình vuông có cạnh là \(\left( {x + 400} \right)\) mét. Hãy tính diện tích phần đất còn lại sau khi đào ao.

Gia đình bác Nam có một khu đất hình chữ nhật, một cạnh đã được xây tường bao (như hình vẽ). Trên khu đất này, bác Nam định cải tạo một phần đất để trồng rau có dạng hình chữ nhật. Tận dụng tường bao đã có và \(40\,\,{\rm{m}}\) lưới B40, bác muốn vây ba mặt còn lại của phần đất trồng rau. Hỏi bác có thể vây kín được phần đất trồng rau có diện tích lớn nhất là bao nhiêu mét vuông?