Đề cương ôn tập cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới (Tự luận) có đáp án - Phần 2

Cho tam giác \(ABC\;\) vuông tại \(A\)\(\left( {AB < AC} \right)\) có \[AM\] là đường trung tuyến. Gọi \(D,\;\,\,E\) lần lượt là hình chiếu của \(M\) trên cạnh \(AB,\;\,\,AC.\)

     a) Chứng minh tứ giác \(ADME\) là hình chữ nhật, từ đó suy ra \(AE = DM.\)

     b) Kẻ đường cao \(AH\)\(\left( {H \in BC} \right)\) của \({\rm{\Delta }}ABC.\) Chứng minh tứ giác \(DHME\) là hình thang cân.

     c) Lấy điểm \(N\) sao cho \(M\) là trung điểm của \(NE.\) Kẻ \(EK\) vuông góc với \(BC.\) Chứng minh \(AK \bot KN.\)

Cho tam giác \(ABC\) có \(AB < AC,\)\(AI\) là đường cao và 3 điểm \(D,\,\,\,E,\,\,\,F\) theo thứ tự là trung điểm của các đoạn thẳng \(AB,\,\,\,AC,\,\,\,BC.\) Lấy \(J\) sao cho \(E\) là trung điểm \[IJ.\]

     a) Tứ giác \[AICJ\] là hình gì? Vì sao?

     b) Chứng minh tứ giác \(DEFI\) là hình thang cân.

     c) \(EB\) và \(FD\) cắt nhau tại \(K.\) Chứng minh hai tứ giác \(ADKE\) và \(KECF\) có diện tích bằng nhau.

     d) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(BDEF\) là hình thoi, là hình vuông.

     e) Giả sử \(DF \bot IE\). Chứng minh: \(DE + IF = AI\).

     g) Gọi \(H\), \(G\) lần lượt là trung điểm của \(BI\) và \(IC\). Chứng minh: \(HE = DG\).

Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau (làm tròn kết quả đến hàng phần mười):

Cho tam giác \(ABC\) vuông tại \(A\,\,\left( {AB < AC} \right).\) Gọi \(I\) là trung điểm của cạnh \(BC.\) Qua \(I\) vẽ \(IN\) vuông góc với \(AC\) tại \(N.\)Lấy điểm \(D\) sao cho \(N\) là trung điểm của \(ID.\)

     a) Chứng minh \(N\) là trung điểm của \(AC\) và tứ giác \(ADCI\) là hình thoi.

     b) Đường thẳng \(BN\) cắt cạnh \(DC\) tại \(K.\) Chứng minh \(\frac{{DK}}{{DC}} = \frac{1}{3}.\)

Cho \(\Delta ABC\) có trung tuyến \(AD.\) Vẽ tia phân giác của \[\widehat {ADB}\] cắt \(AB\) tại \(M,\) tia phân giác của \[\widehat {ADC}\] cắt \(AC\) tại \(N.\) Chứng minh rằng:

a) \[\frac{{MB}}{{MA}} = \frac{{BD}}{{AD}}.\]            

b) \[\frac{{MB}}{{MA}} = \frac{{NC}}{{NA}}.\]                     

c) \(MN\,{\rm{//}}\,BC.\)

Cho tam giác \(ABC\) có \(AB < AC.\) Tia phân giác \(\widehat {BAC}\) cắt cạnh \(BC\) tại điểm \(D.\) Gọi \(M\) là trung điểm của cạnh \(BC.\) Qua điểm \(M\) kẻ đường thẳng song song với đường thẳng \(AD\) cắt các đường thẳng \(AC,\,\,AB\) lần lượt tại \(E\) và \(K.\)Chứng minh rằng:

     a) Tam giác \(AEK\) cân.         b) \(\frac{{AK}}{{EC}} = \frac{{DM}}{{MB}}.\)            c) \(BK = EC.\)

Cho tứ giác \[ABCD.\] Gọi \[E,{\rm{ }}F,{\rm{ }}I\;\] theo thứ tự là trung điểm của \(AD,\,\,BC,\,\,AC.\) Chứng minh rằng:

     a) \[EI\,{\rm{//}}\,CD\] và \[IF\,{\rm{//}}\,AB.\]                    b) \[EF \le \frac{{AB + CD}}{2}.\]

Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\)\(E\) là giao điểm của \(MA\) và \(BD,\)\(F\) là giao điểm của \(MB\) và \(AC.\)

     a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]

     b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\) Chứng minh \(HE = EF = FN.\)

     c) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)

Cho \(\Delta ABC\) có trung tuyến \(AD\), trọng tâm \(G,\) đường thẳng đi qua \(G\) cắt các cạnh \(AB,\,\,AC\) lần lượt tại \(E,\,\,F.\) Từ \(B,\,\,C\) kẻ các đường song song với \(EF\) cắt \(AD\) lần lượt tại \(M,\,\,N.\) Chứng minh rằng:

     a) \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}.\)              b) \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1.\)                  c) \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = 3.\)

Cho tam giác \(ABC\) có \(BC = 15{\rm{\;cm}},\,\,CA = 18{\rm{\;cm}}\) và \(AB = 12{\rm{\;cm}}.\) Gọi \(I\) và \(G\) lần lượt là tâm đường tròn nội tiếp và trọng tâm \(\Delta ABC.\)

     a) Chứng minh \(IG\,{\rm{//}}\,BC.\)              b) Tính độ dài đoạn thẳng \(IG.\)

Vì kèo mái tôn là một trong những bộ phận không thể thiếu trong cấu tạo mái nhà lợp tôn. Nó giúp chống đỡ và giảm trọng lực của những ảnh hưởng từ các yếu tố bên ngoài tác động vào (Hình a).

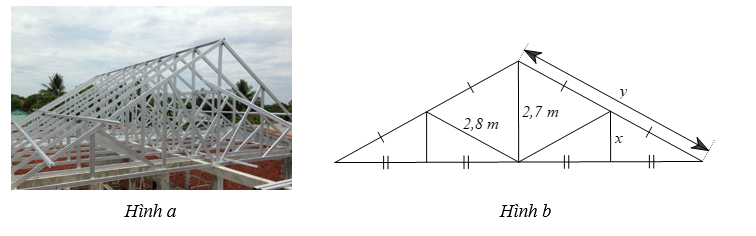
Một vì kèo mái tôn được vẽ lại như Hình b. Tính độ dài \(x\) của cây chống đứng bên và độ dài \(y\) của cánh kèo.