Đề cương ôn tập cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới (Đúng sai - Trả lời ngắn) có đáp án

Cho hai đa thức:

\(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\) và \[B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}.\]

Đa thức \(M\) thỏa mãn \(A = M + B.\)

a) Bậc của đa thức \[A\] là 8.

b) Hệ số tự do của đa thức \(B\) là 2.

c) Giá trị của biểu thức \(B\) tại \[x = - 1\,;\,\,y = 1\] là 12.

d) \(M\)là một đơn thức.

Một sân bóng hình chữ nhật có chiều dài \(15x + 5y{\rm{ }}\left( {\rm{m}} \right)\) và chiều rộng là \(10x - 5y{\rm{ }}\left( {\rm{m}} \right)\). Mỗi cạnh chừa lại \({\rm{3 m}}\) làm lối đi. Phần trong là sân trồng cỏ phục vụ cho các trận đấu.

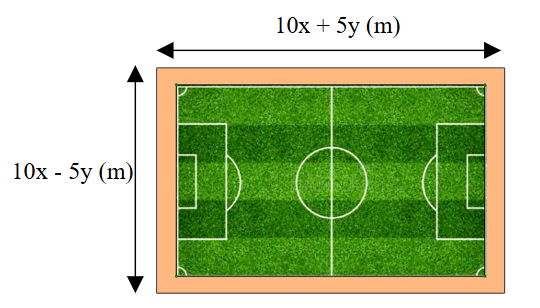
a) Chiều dài của mặt sân trồng cỏ là \(10x - 5y - 6{\rm{ }}\left( {\rm{m}} \right).\)

b) Chiều rộng của mặt sân trồng cỏ là \(10x + 5y - 6{\rm{ }}\left( {\rm{m}} \right).\)

c) Biểu thức biểu diễn diện tích của mặt sân trồng cỏ là \(S = 100{x^2} - 25{y^2} - 120x + 36{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

d) Diện tích của mặt sân trồng cỏ khi \(x = 9{\rm{ m}},\,\,y = 3{\rm{ m}}\) có giá trị lớn hơn \(6800{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)

Cho \(A = {a^3} - {b^3} + 5ab + 5{a^2} + 5{b^2}.\)

a) \(A = \left( {{a^2} - ab + {b^2}} \right)\left( {a - b + 5} \right).\)

b) Nếu \(a - b = - 5\) thì giá trị biểu thức \(A\) bằng \(0.\)

c) Nếu \(a - b = 10\) thì $A\cancel{⋮}5.$

d) Nếu \({a^2} + {b^2} = - ab\) thì giá trị của biểu thức \(A\) bằng \(1.\)

Chị Lan đã ghi lại khối lượng bán được của mỗi loại mà sạp hoa quả của chị bán được trong ngày và biểu diễn trong biểu đồ dưới đây:

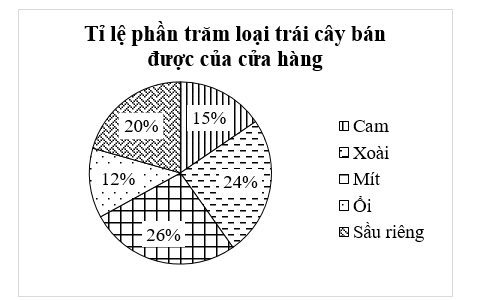
a) Chị Lan đã thu thập dữ liệu của biểu đồ trên bằng phương pháp thu thập gián tiếp.

b) Từ biểu đồ hình quạt tròn, ta có bảng thống kê sau:

c) Số kilôgam sầu riêng mà sạp hoa quả của chị Lan đã bán được trong ngày hôm đó là \(40{\rm{ kg}}{\rm{.}}\)

d) Số kilôgam Xoài bán được nhiều hơn Sầu riêng là \({\rm{12 kg}}{\rm{.}}\)

Biểu đồ cột kép ở hình bên dưới biểu diễn giá trị xuất khẩu, nhập khẩu hàng hóa nước ta trong quý I giai đoạn 2020 – 2022 như sau:

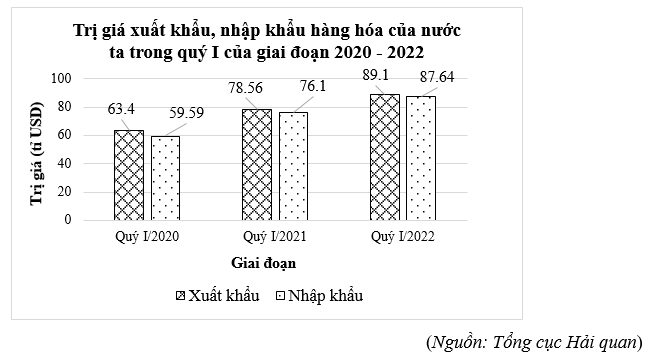
(Nguồn: Tổng cục Hải quan)

a) Dữ liệu ở biểu đồ trên được thu thập bằng phương pháp thu thập gián tiếp.

b) Từ biểu đồ trên, ta có bảng thống kê là:

c) Tổng giá trị xuất khẩu hàng hóa nước ta trong quý I giai đoạn 2020 – 2022 nhỏ hơn \(230\) tỉ USD.

d) Giá trị xuất khẩu hàng hóa của nước ta trong quý I/2021 tăng khoảng \(19,3\% \) so với quýI/2020.

Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AM\), \(N\) là trung điểm của \(AC\). Kẻ \(Ax\parallel BC\) cắt \(MN\) tại \(E\).

a) \(M\) là trung điểm của \(BC.\)                   b) \(ME\parallel AB.\)

c) \(AE = MC.\)                                              d) $\mathrm{\Delta AEN}\backsim \mathrm{\Delta CNM}$.

Cho tam giác \(ABC\) có đường cao \(AH\). Kẻ \(HE \bot AB\) tại \(E\) kéo dài lấy \(ME = HE\). Kẻ \(HF \bot AC\) tại \(F\), kéo dài \(HF\) lấy \(FN = FH\). Gọi \(I\) là trung điểm của \(MN\).  

a) \(AB\) là trung trực của \(NH.\)                  b) \(EF\parallel MN.\)

c) \(\Delta AMN\) cântại \(M.\)                   d) \(AI \bot EF.\)

Cho tam giác \[ABC\] có \[AM\] là đường trung tuyến. Lấy \[D\] thuộc \[AC\] sao cho \[AD = \frac{1}{2}DC\]. Kẻ \[ME\parallel BD\]\[\left( {E \in DC} \right)\], \[BD\] cắt \[AM\] tại \[I\].

a) \[AD = \frac{1}{2}DE.\]                          b) \[I\] là trung điểm của \[AM\].

c) \[{S_{AIB}} = {S_{IMB}}.\]                d) \[{S_{ABC}} = 3{S_{IBC}}.\]

Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\,,\) đường cao \(AH\,.\) Từ \(H\) kẻ \(HM \bot AB\,\,\left( {M \in AB} \right)\,.\) Kẻ \(HN \bot AC\,\,\left( {N \in AC} \right)\,.\) Trên tia đối của tia \[MH\] lấy điểm \[P\] sao cho \[M\] là trung điểm của \[PH.\] Gọi \(I\) là trung điểm của \(HC\,,\) lấy \(K\) trên tia \(AI\) sao cho \(I\) là trung điểm của \(AK;\,\,MN\)  cắt \(AH\) tại \(O,\)\(CO\) cắt \(AK\) tại \(D.\)

a) \(\widehat {HKC} = \frac{1}{2}\widehat {HAC}\).                                                                  

b) Tứ giác \[AMHN\] là hình chữ nhật.

c) Tứ giác \(MNCK\)là hình thang vuông.             

d) \(AK = 2AD\).

Cho các đơn thức sau: \(\sqrt 5 ;{\rm{ }}{x^2};{\rm{ }}\frac{{{5^2}}}{{98}}{y^4};{\rm{ }} - \sqrt 7 x{y^2}{z^3}y;{\rm{ }}\frac{{\sqrt 2 }}{{11}}xy{z^2}z.\) Có bao nhiêu đơn thức không là đơn thức thu gọn?

Hai người đi xe đạp cùng một lúc và ngược chiều nhau từ hai địa điểm A và B. Người xuất phát từ A đi với vận tốc không đổi \(x{\rm{ }}\left( {{\rm{km/h}}} \right)\). Người xuất phát từ B đi với vận tốc không đổi \(y{\rm{ }}\left( {{\rm{km/h}}} \right)\). Hai người gặp nhau tại C sau 4 giờ. Tính quãng đường AB tại \(x = 10;y = 8\) (Đơn vị: km).

Khi rút gọn biểu thức \({\left( {1 + 2x} \right)^3} + {\left( {2x - 1} \right)^3}\) ta thu được một đa thức có bao nhiêu hạng tử?

Cho hai số \(x\,,\,\,y\) thỏa mãn\(x - y = 5\) và \(xy = 3\). Tính giá trị\({x^2} + {y^2}\).

Lượng tinh bột sẵn mà các thị trường cung cấp cho Đài Loan trong 9 tháng năm 2022 được thống kê trong bảng dưới đây.

(Nguồn: Theo thống kê của cơ quan Tài chính Đài Loan)

Thị trường Việt Nam cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 chiếm bao nhiêu phần trăm so với tổng lượng tinh bột sắn mà các thị trường cung cấp cho Đài Loan trong 9 tháng năm 2022?

(Kết quả làm tròn đến hàng phần mười)

Biểu đồ đoạn thẳng dưới đây biểu diễn sản lượng thủy sản của nước ta qua các năm 2010; 2014; 2016; 2018; 2020 (đơn vị: nghìn tấn).

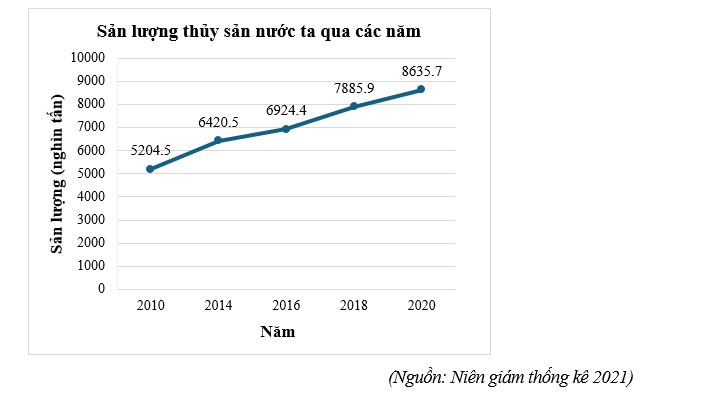
Hỏi sản lượng thủy sản của nước ta năm 2020 chiếm bao nhiêu phần trăm tổng sản lượng thủy sản của nước ta qua các năm? (Kết quả làm tròn đến hàng phần mười)

Tứ giác \(ABCD\) có \(\widehat C = 50^\circ ,\,\,\widehat D = 60^\circ ,\,\,\widehat A:\widehat B = 3:2.\) Tính \(2\widehat A - \widehat B\) (đơn vị: độ).

Cho tứ giác \[ABCD\] có \(\widehat A = 50^\circ \,;\,\,\widehat B = 130^\circ \,;\,\,\widehat C = 80^\circ \). Tính số đo của \(\widehat D\) (đơn vị: độ).

Cho hình thang cân \[ABCD,\] đáy lớn \[BC.\] Biết\(\widehat A - 2\widehat B = 30^\circ .\)Tính số đo góc tại đỉnh \[D\] của hình thang (đơn vị: độ).

Hình thang cân \(ABCD\)\(\left( {AB\,{\rm{//}}\,CD} \right)\) có \(\widehat C = 60^\circ \). Tính \(\widehat A - \widehat C\)(đơn vị: độ).