Đề cương ôn tập giữa kì 1 Toán 8 Kết nối tri thức cấu trúc mới (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trắc nghiệm đúng sai
Cho hai biểu thức \(A\) và \(B\) thỏa mãn \(45{x^6}{y^3}:A = 5x{y^2}\) và \(\left( {B + 7{x^4}{y^2}} \right):A = 3x{y^2} + 2xy\).
a) Biểu thức \(A\) là đơn thức bậc 3.
b) Với \(x = - 1\,;\,\,y = 2\) thì giá trị của biểu thức \(A\) bằng \( - 18.\)
c) \(B = 27{x^4}{y^4} + 11{x^4}{y^2}\).
d) Tích của hai biểu thức \(A\) và \(B\) là \(36{x^7}{y^5} + 20{x^7}{y^3}.\)
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)
Đa thức \(M\) và \(P\) thỏa mãn
a) Hạng tử tự do của đa thức \(A\) là \( - 4\).
b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)
c) \(M = {x^2} + 7xy + {y^2}.\)
d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).
Cho hai đa thức:
\(M = 23{x^{23}}y - 22x{y^{23}} + 21y - 1\) và \(N = - 22x{y^3} - 42y - 1\).
a) Biểu thức \(M\) là đa thức có bậc 23.
b) Với \(x = 0\,;\,y = - 2\) thì giá trị của biểu thức \(N\) là 83.
c) \(M - N = 23{x^{23}}y - 22x{y^{23}} + 22x{y^3} + 63y\).
d) Để \(M - N - P = 63y + 1\) thì \(P = 23{x^{23}}y - 22x{y^{23}} + x{y^3} + 1\).
Cho hai đa thức \(P = {x^2} - 4xy + 9\) và \(Q = - 6xy - 4{y^2} + 9.\)
Đa thức \(A\) và \(M\) thỏa mãn
a) Với \(x = 1\,;\,\,y = - 1\) thì giá trị của biểu thức \(P\) bằng 10.
b) Đa thức \(Q\) có bậc là 2.
c) \[A = {x^2} + xy + 4{y^2}.\]
d) Giá trị của biểu thức \(M\) không phụ thuộc vào biến \(x.\)
Cho đa thức \(A = 3{x^2}y - 2x{y^2} - 4xy + 1.\)
Đa thức \(B\) và \(M\) thỏa mãn
a) Với \[x = - 1\,;\,\,y = 1\] thì giá trị của biểu thức \(A\) bằng 9.
b) Đa thức \(B\) sau khi thu gọn có 5 hạng tử.
c)Đa thức \(M\)có bậc là 2.
d) Tổng của hai đa thức \(B\) và \(M\) có hạng tử tự do là 1.
Cho hai đa thức:
\(A = {x^2}y + 5xy - 1\) và \(B = 3y\left( {3y - x} \right) + \left( { - 2{x^2}{y^2} - 6x{y^3} + 4xy} \right):\frac{2}{3}xy\).
a)Đa thức \(A\)có bậc là 2.
b) Đa thức \(B\)không chia hết cho 6.
c) Với \(x = \frac{1}{2};\)\(y = 4\) thì \(B = - 6\).
d) Tổng của hai đa thức \(A\) và \(B\) có hạng tử tự do là 6.
Cho hình bình hành \(ABCD\) có \(BC = 2AB\), \(\widehat A = 60^\circ \). Gọi \(E\), \(F\) theo thứ tự là trung điểm của \(BC\), \(AD\). Trên tia \(AB\) lấy điểm \(I\)sao cho \(B\)là trung điểm của \(AI.\)
a) \(AB = \frac{2}{3}BE\).
b) Tứ giác \(ABEF\) là hình chữ nhật.
c) Tam giác \(ADI\) cân tại \(D\).
d) \(\widehat {AED} = 90^\circ \).
Cho tam giác \[ABC\] cân tại \[A,{\rm{ }}AH\] là đường cao. Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[AB,{\rm{ }}AC\]. Gọi \[D,{\rm{ }}E\] lần lượt là điểm sao cho \[M\] là trung điểm của \[HD,{\rm{ }}N\] là trung điểm của \[HE.\]
a) \[BH = HC\].
b) Tứ giác \[AHBD\] là hình thoi.
c) Giao điểm của \[BE\] và \[CD\] là trung điểm của \[AH\].
d) \[2DH = 3HE\].
Cho \[\Delta ABC\] cân tại \[A,\] trung tuyến \[AM,\;\]\[I\] là trung điểm \[AC.\] Gọi \[N\] là điểm đối xứng của \[M\] qua \[I\].Gọi \[E,\,\,K\] lần lượt là trung điểm \[AM,\,\,AB.\]
a) Tứ giác \[AMCN\] là hình thoi.
b) \[E\] là trung điểm \[BN.\]
c) \(AK = AI.\)
d) Điều kiện của \[\Delta ABC\] để tứ giác \[AKMI\] là hình vuông thì \(\widehat {KAI} = 45^\circ .\)
Cho tam giác \[ABC\] không vuông tại \[A\]. Dựng bên ngoài tam giác đó hai tam giác \[ABD,{\rm{ }}ACE\] vuông cân tại đỉnh \[A\] rồi dựng hình bình hành \[AEID\]. Biết \[\widehat {DAI} = \widehat {ABC}\]. Gọi \[K\] là trung điểm của \[BD.\]
a) \[\widehat {DAI} + \widehat {BAH} = 45^\circ \].
b) \[AI \bot BC\].
c) \(\widehat {EBA} = \frac{1}{2}\widehat {CDA}\).
d) \(\widehat {IKC} = 90^\circ \).
Trắc nghiệm trả lời ngắnTính giá trị của đa thức \(A = 7{x^2}y - 4{x^6} + 3{y^2}z + 4{x^6}\) tại \[x = 2\,;{\rm{ }}y = 1.\]
Cho \(B - \left( {5{x^2} - 2xyz} \right) = 2{x^2} + 2xyz + 1\). Hạng tử tự do của đa thức \(B\) là bao nhiêu?
Kết quả của phép chia \(\left( {5{x^5}{y^4}z + \frac{1}{2}{x^4}{y^2}{z^3} - 2x{y^3}{z^2}} \right):\frac{1}{4}x{y^2}z\) là đa thức bậc mấy?
Giá trị của biểu thức \[A = {\left( {3x + 1} \right)^2} + {\left( {3x-1} \right)^2}-2\left( {3x-1} \right)\left( {3x + 1} \right)\] bằng
Xác định nghiệm nhỏ nhất của phương trình \[{\left( {x-3} \right)^2} + 3-x = 0\]
Cho biểu thức \[{x^3} + 6{x^2} + 12x + m\] là lập phương của một tổng. Tính giá trị của\(m\).
Cho tứ giác \(ABCD\) có \[\widehat C = 60^\circ ,\,\,\widehat D = 80^\circ ,\,\,\widehat A - \widehat {B\,} = 10^\circ .\]Tính số đo của \(\widehat {A\,}\) (đơn vị: độ).
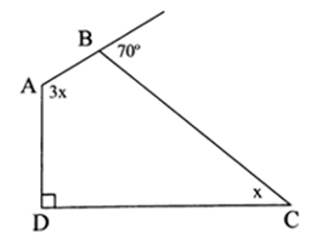
Cho hình vẽ bên. Tính số đo \(3x\) trong hình vẽ bên.
Tứ giác \[ABCD\] có số đo các góc \[\widehat A\,;\,\,\widehat B\,;\,\,\widehat C\,;\,\,\widehat D\] tỉ lệ thuận với \[4\,;\,\,3\,;\,\,5\,;\,\,6\]. Tính số đo \[\widehat A\] (đơn vị: độ)
Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\].
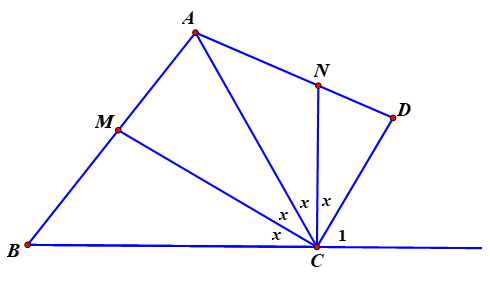
Tính số đo góc \[\widehat {{C_1}}\] (đơn vị: độ).








