Đề cương ôn tập cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới (Tự luận) có đáp án - Phần 3

Lúc 6 giờ sáng, bạn Hải đi xe đạp từ điểm \[A\] đến trường (tại điểm \(B)\) phải leo lên và xuống một con dốc với đỉnh dốc tại điểm \[C\] (như hình vẽ).

Điểm \(H\) là một điểm thuộc đoạn thẳng \[AB\] sao cho \[CH\] đường là phân giác \(\widehat {ACB},\)\[AH = 0,32{\rm{\;km}}\] và \[BH = 0,4{\rm{\;km}}.\] Biết bạn Hải đi xe đạp đến \[C\] lúc 6 giờ 30 phút với tốc độ trung bình lên dốc là 4 km/h. Hỏi bạn Hải đến trường lúc mấy giờ nếu tốc độ trung bình xuống dốc là 10 km/h?

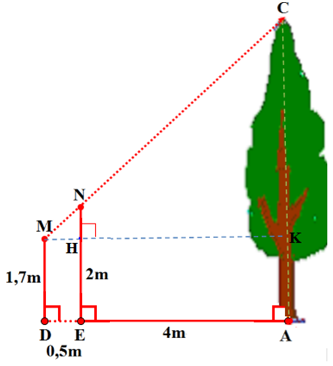
Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao \(2\,\,{\rm{m}}\) và đặt xa cây \(4\,\,{\rm{m}}.\) Sau khi người ấy lùi ra xa cách cọc \(0,5\,\,{\rm{m}}\) thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng (như hình vẽ). Hỏi cây cao bao nhiêu, biết khoảng cách từ chân đến mắt người ấy là \(1,7\,\,{\rm{m}}.\)

Em hãy đề xuất phương pháp thu thập dữ liệu cho các vấn đề sau và cho biết phương pháp thu thập đó là gián tiếp hay trực tiếp:

     a) Tên 10 tỉnh/ thành phố có diện tích lớn nhất Việt Nam.

     b) Các món ăn được UNESCO công nhận là văn hóa phi vật thể.

     c) Loại trái cây yêu thích của học sinh lớp 8A được dùng trong tiệc liên quan cuối năm.

Ghép các dữ liệu với loại dữ liệu thích hợp.

1) Bạn An muốn thu thập dữ liệu về số các bạn nữ ở tất cả các lớp trong khối 8 của trường.

     a) Bạn An có thể thu thập bằng phương pháp trực tiếp hay gián tiếp?

     b) Dữ liệu thu được thuộc loại nào?

2) Sau khi thu thập bạn có được bảng thống kê về số học sinh nữ trong từng lớp của khối 8 như bảng dưới đây:

     a) Hãy vẽ biểu đồ đoạn thẳng thể hiện bảng thống kê trên.

     b) Hãy vẽ biểu đồ hình quạt tròn thể hiện bảng thống kê trên.

Một cửa hàng quần áo đưa ra chương trình khuyến mãi giảm giá một số mặt hàng sau: Quần âu giảm giá \(25\% ;\) Áo sơ mi giảm \(35\% ;\) Áo khoác giảm \(20\% ;\) Quần Jean giảm \(10\% .\)

     a) Trong các mặt hàng trên, sản phẩm nào được giảm giá nhiều nhất, ít nhất và với mức giảm giá bao nhiêu phần trăm?

     b) Bạn An đã biểu diễn tỉ lệ giảm giá của các mặt hàng trên bằng biều đồ hình quạt tròn. Biểu đồ An sử dụng có phù hợp không?

     c) An nên dùng biểu đồ nào để biểu diễn ? Hãy vẽ biểu đồ đó.

     d) Mẹ An đã mua \(2\) chiếc áo sơ mi với giá mỗi chiếc áo sau khi giảm là \(325\,\,000\) đồng và \(4\) chiếc quần âu. Tổng số tiền mẹ An thanh toán tại quầy là \(1\,\,850\,\,000\) đồng. Em hãy tính xem mỗi chiếc áo sơ mi và quần âu nguyên giá sẽ là bao nhiêu tiền.

Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của trường:

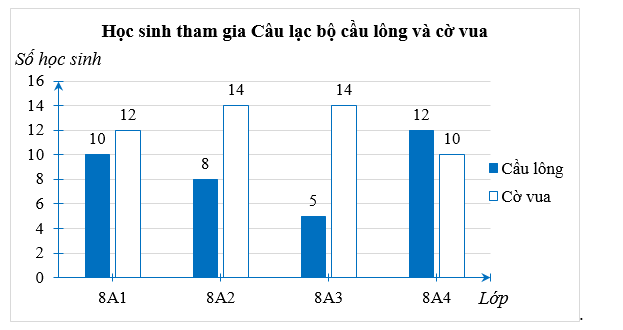
a) Lập bảng thống kê cho biểu đồ trên.

b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.

c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm \(25\% \) tổng số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.

d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua.

Cho hai biểu đồ dưới đây:

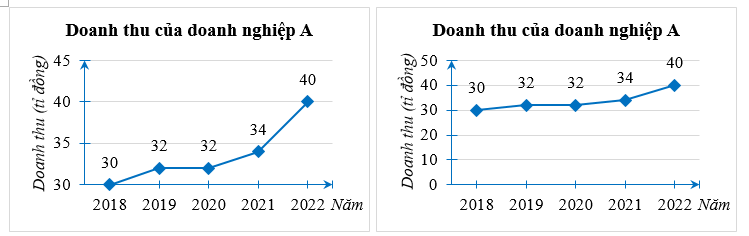
a) Dữ liệu biểu diễn trên hai biểu đồ có như nhau không? Nếu có hãy lập bảng thống kê cho dữ liệu đó.

b) Có thể căn cứ vào độ dốc trên hai đường gấp khúc trên hai biểu đồ để đánh giá về tốc độ doanh thu trong 5 năm của các dữ liệu được biểu diễn không? Tại sao?

Biểu đồ hình quạt tròn ở hình bên biểu diễn tỉ lệ các yếu tố ảnh hưởng đến sinh trưởng của cây trồng như: Phân bón, Nước tưới, Giống, Kiểm soát dịch hại, Kiểm soát cỏ dại, Yếu tố khác.

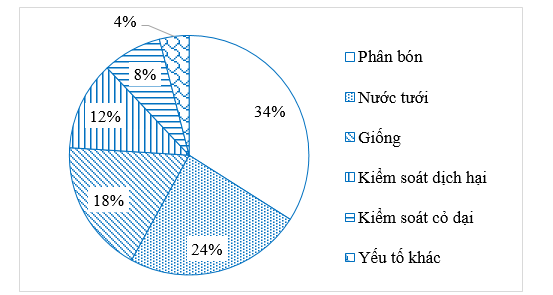
a) Cho biết yếu tố nào ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất?

b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì yếu tố Kiểm soát dịch hại gấp mấy lần Yếu tố khác?

c) Vấn đề tưới nước cho cây cũng là một yếu tố quan trọng ảnh hưởng đến sinh trưởng của cây trồng. Em hãy đề xuất một vài biện pháp khắc phục tình trạng trên để làm giảm thiệt hại trong việc trồng trọt.

Biểu đồ đoạn thẳng ở hình bên dưới thống kê số lượng gia cầm ở TP. HCM và Kon Tum qua các năm 2015, 2018, 2019, 2020. (Nguồn: Niêm giám thống kê năm 2021).

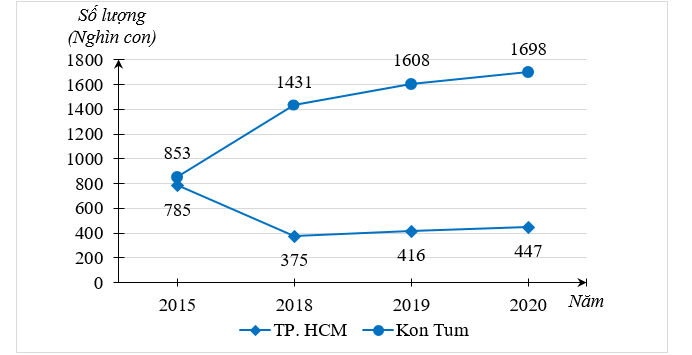
a) Hãy hoàn thành biểu đồ cột kép ở hình bên dưới để nhận được biểu đồ biểu diễn dữ liệu trong biểu đồ đoạn thẳng ở hình trên.

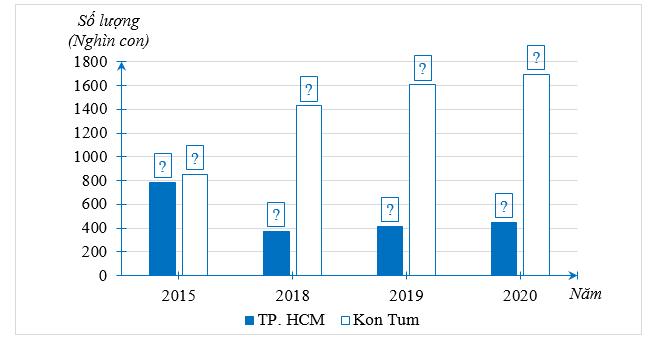
b) TP. HCM và Kon Tum trong năm 2020 lượng gia cầm ở đâu nhiều nhất? Nhiều nhất là bao nhiêu nghìn con?

c) Một bài báo đã nêu ra nhận định “Tổng số lượng gia cầm ở Kon Tum trong năm \[2015,\]\[2018,{\rm{ }}2019,{\rm{ }}2020\] là \[2023\] nghìn con và so với năm \[2018\] số lượng gia cầm ở TP. HCM tăng \(80\% \) so với số lượng gia cầm ở Kon Tum”. Em hãy cho biết nhận định trên bài báo có chính xác không?

d) Em hãy đề xuất một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những năm tới để đạt hiệu quả trong chăn nuôi.

Thống kê tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định từ tháng 1 đến tháng 12 lần lượt là: \[34,4;{\rm{ }}27,5;{\rm{ }}49,4;{\rm{ }}108,2;{\rm{ }}88,8;{\rm{ }}186,6;{\rm{ }}190,7;\]\[151,7;\]\[133,2;\]\[165,0;\]\[126,2;\]\[102,1\] (đơn vị: giờ) (Nguồn: Tổng cục thống kê).

a) Lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định theo mẫu sau:

b) Hãy hoàn thành biểu đồ hình bên dưới để nhận được biểu đồ đoạn thẳng biểu diễn tổng số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định.

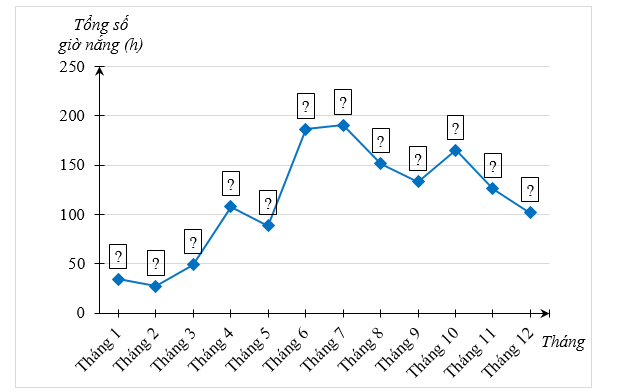
c) Tổng số giờ nắng tại trạm quan trắc Nam Định trong tháng nào cao nhất? Thấp nhất?

d) Hãy nhận xét về sự thay đổi số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định trong các khoảng thời gian: tháng 1 – tháng 2; tháng 2 – tháng 3; tháng 3 – tháng 4; tháng 4 – tháng 5; tháng 5 – tháng 6; tháng 6 – tháng 7; tháng 7 – tháng 8; tháng 8 – tháng 9; tháng 9 – tháng 10; tháng 10 – tháng 11; tháng 11 – tháng 12.

e) Một bài báo có nêu thông tin: “So với tháng 9, tổng số giờ nắng tại trạm quan trắc Nam Định trong tháng 10 tăng lên xấp xỉ 34%”. Thông tin của bài báo đó có chính xác không?

Cho x và y thoả mãn: \({x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0\). Tính giá trị của biểu thức:

\(A = \frac{{{{\left( {x + y - 4} \right)}^{2222}} - {y^{2222}}}}{x}.\)

Cho x và y thoả mãn: \[{x^2} + 2xy + 6x + 6y + 2{y^2} + 8 = 0\]. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức \[M = x + y + 6\].

Chứng minh rằng

     a) Nếu \[x\] là số tự nhiên không chia hết cho \[3\] thì \(M = 2{x^2} - 5\) chia hết cho \[3\].

     b) Nếu \(x\) là số tự nhiên lẻ thì \(N = {x^3} + 3{x^2} - x - 3\) chia hết cho \[8\].

     c) Đa thức \[M = x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1\] (với \(x \in \mathbb{Z}\)) là bình phương của một số nguyên.

Cho ba số thực \(a,\,\,b,\,\,c\) khác \(2\) và thỏa mãn \(a + b + c = 6.\) Tính giá trị của biểu thức:

\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}.\)

Cho ba số thực \(x,y,z \ne 0\) và \(x + y + z = 0\). Tính giá trị của biểu thức

\(T = \frac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {y^2}}}\).

Bác Bảy có một trang trại lớn để trồng rau và chăn nuôi gia cầm. Bác dự định mua một tấm lưới thép B40 để rào bao quanh khu vực nuôi gia cầm của trang trại với thiết kế có dạng hình chữ nhật \(ABCD\)(như hình mô tả ở bên). Biết rằng, bác Bảy không rào xung quanh khu vực nhà kho và vị trí nhà kho cố định. Với số tiền của mình, bác Bảy chỉ mua được tấm lưới có chiều dài \(500\,\,{\rm{m}}\). Hỏi bác Bảy sẽ dựng rào chắn như thế nào để diện tích khu nuôi gia cầm là lớn nhất?

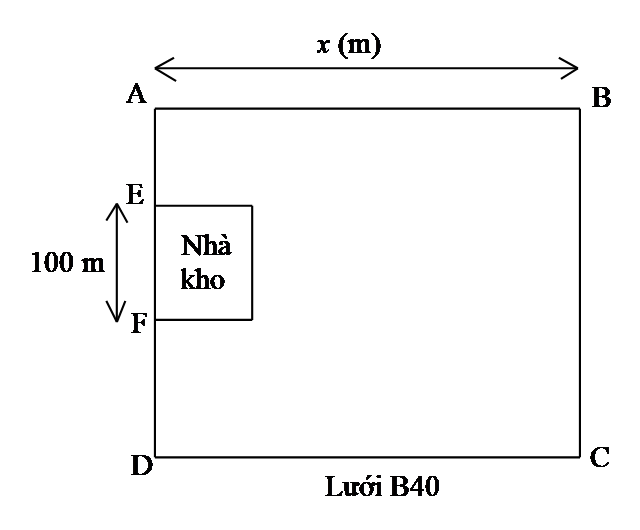
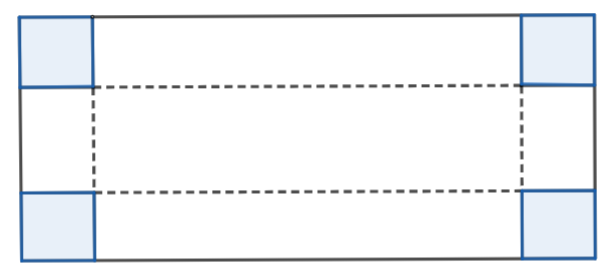
Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\) và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{\;(cm)}}\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.