Đề cương ôn tập giữa kì 1 Toán 8 Kết nối tri thức cấu trúc mới (Trắc nghiệm) có đáp án
30 câu hỏi
Trong các đơn thức sau: \( - 2xy\;;\;3{x^2}y\;;\; - 4{x^2}{y^2}\;;\;\frac{5}{2}{x^2}y\;;\;12{x^2}\). Số đơn thức đồng dạng với đơn thức \( - \frac{3}{2}{x^2}y\) là
\(1\).
\(2\).
\(3\).
\(4\).
Bậc của biểu thức \(A = 2{x^2}y \cdot 5x{y^3}\) là
\(5\).
\(6\).
\(7\).
\(8\).
Thu gọn đa thức \(x{y^3} + 4x{y^3} - 2x{y^3}\) được kết quả là
\(3x{y^3}\).
\( - 2x{y^3}\).
\(2x{y^3}\).
\(3{x^3}{y^6}\).
Giá trị của biểu thức\(B = 16{x^2}{y^5} - 2{x^3}{y^2}\) tại \(x = - 1\) và \(y = 1\) là
\(16\).
\(17\).
\(18\).
\(20\).
Kết quả phép nhân hai đơn thức \(x\left( {2{x^2}} \right)\) là
\(2{x^2}\).
\(3{x^3}\).
\({x^3}\).
\(2{x^3}\).
Rút gọn biểu thức \(\left( {x + y} \right) + \left( {x + z} \right) - \left( {y + z} \right)\)có kết quả là
\(0\).
\(2x\).
\( - 2z\).
\( - 2y\)
Kết quả của phép tính \(x\left( {2{x^2} + 1} \right)\)là
\(3{x^2} + x\).
\(3{x^3} + x\).
\(2{x^3} + x\).
\(2{x^3} + 1\).
Đa thức\(A = 5{x^2}y + x{y^3}\) có bậc mấy?
\(5\).
\(4\).
\(3\).
\(2\).
Đa thức \(C = 4{x^2}{y^3} - x{y^2} + 3 - 4{x^2}{y^3} + x{y^2}\) có bậc mấy?
\(0\).
\(1\).
\(3\).
\(4\)
Kết quả phép cộng hai đơn thức \(2xy + 5xy\) là
\(7xy\).
\(10{x^2}{y^2}\).
\(7{x^2}{y^2}\).
\(10xy\)
Đơn thức \(25a{x^4}{y^3}z\) (với \(a\) là hằng số) có
hệ số là \(25\), phần biến là \[a{x^4}{y^3}z.\]
hệ số là \(25\), phần biến là \[{x^4}{y^3}z.\]
hệ số là \(25a\), phần biến là \[{x^4}{y^3}z.\]
hệ số là \(25a\), phần biến là \[a{x^4}{y^3}z.\]
Điều kiện của số tự nhiên \(n\) để phép chia \({x^5}{y^n}:{x^n}{y^3}\) là phép chia hết là
\(n = 3\).
\(n = 4\).
\(n = 5\).
\(n \in \left\{ {3\,;\,\,4\,;\,\,5} \right\}\).
Giá trị nhỏ nhất của biểu thức \(C = 16{x^2} + 2{\left( {y + 2} \right)^2} - 3\) là
\(16\).
\(18\).
\( - 3\).
\(15\).
Điều kiện của số tự nhiên \(n\) để phép chia \(\left( {4{x^{10}}y - x{y^7} + {x^5}{y^4}} \right):2{x^n}{y^n}\) là phép chia hết là
\(n = 0\).
\(n = 1\).
\(n = 5\).
\(n \in \left\{ {0\,;\,\,1} \right\}\).
Nhân hai đơn thức \( - 3{x^3}{y^2}\) và \(\frac{1}{9}xy\) ta được kết quả là
\( - \frac{1}{3}{x^4}{y^3}\).
\(\frac{1}{3}{x^4}{y^3}\).
\( - \frac{1}{3}{x^4}{y^2}\).
\( - \frac{1}{3}{x^4}{y^4}\).
Khai triển \({\left( {2x - 3} \right)^2}\) ta được
\(2{x^2} - 12x + 9\).
\(2{x^2} + 12x + 9\).
\(4{x^2} - 12x + 9\).
\(4{x^2} - 6x + 9.\)
Viết biểu thức \({x^2} - 8x + 16\) dưới dạng bình phương một hiệu là
\[{\left( {x - 16} \right)^2}.\]
\[{\left( {x - 4} \right)^2}.\]
\[{\left( {x - 2} \right)^2}.\]
\[{\left( {x - 8} \right)^2}.\]
Cho hai số \(x\,,\,\,y\) thỏa mãn \(x - y = 5\) và \(xy = 3\). Khi đó giá trị \({x^2} + {y^2}\) là
31.
19.
25.
28.
Giá trị nhỏ nhất của biểu thức \[{x^2} - 4x + 7\] là
\[7\].
\[3\].
\[\frac{1}{3}\].
\[\frac{2}{3}\].
Cho \[{x^2} + {y^2} + 2x + 1 = 0\]. Giá trị của biểu thức \[{\left( {x - y} \right)^{2025}} + {\left( {x + y} \right)^{2026}}\] là
\[2\].
\[1\].
\[0\].
\[ - 1\].
Tứ giác \[ABCD\] có \[\widehat A = 60^\circ \,;\,\,\,\widehat B = 135^\circ \,;\,\,\,\widehat D = 29^\circ \]. Số đo \[\widehat C\] bằng
\[136^\circ \].
\[137^\circ \].
\[36^\circ \].
\[135^\circ \].
Giá trị số đo \[2y - x\] trong hình vẽ là
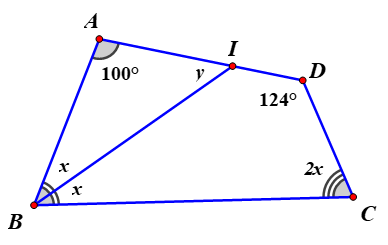
\(46^\circ \).
\(126^\circ \).
\(134^\circ \).
\(58^\circ \).
Một hình thang vuông có một góc bằng \(75^\circ ,\) góc còn lại không vuông của hình thang đó có số đo là
\(25^\circ .\)
\(75^\circ .\)
\(105^\circ .\)
\(125^\circ .\)
Phát biểu nào sau đây là sai?
Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là hình vuông.
Tứ giác có hai đường chéo bằng nhau là hình bình hành.
Tứ giác có 4 cạnh bằng nhau là hình thoi.
Tứ giác có 4 góc bằng nhau là hình chữ nhật.
Tứ giác \(ABCD\) có \(\widehat C = 50^\circ \), \(\widehat D = 60^\circ \), \(\widehat A:\widehat B = 3:2\). Tính \(2\widehat A - \widehat B\).
\({90^{\rm{o}}}\).
\({100^{\rm{o}}}\).
\({200^{\rm{o}}}\).
\({50^{\rm{o}}}\).
Khẳng định nào sau đây là sai?
Tứ giác có hai cạnh đối song song là hình thang.
Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Hình thang cân có hai cạnh bên bằng nhau.
Hình thang có hai cạnh bên bằng nhau là hình thang cân.
Cho hình thang cân \[ABCD\] \(\left( {AB\,{\rm{//}}\,CD} \right)\) có \(\widehat A = 70^\circ \). Kết quả nào sau đây là sai?
\(\widehat D = 110^\circ \).
\(\widehat B = 110^\circ \).
\(\widehat C = 110^\circ \).
\(\widehat B = 70^\circ \).
Hình thang cân \(ABCD\) \(\left( {AB\,{\rm{//}}\,CD} \right)\) có \(\widehat C = 60^\circ \). Khi đó \(\widehat A - \widehat C\) bằng
\[120^\circ \].
\[0^\circ \].
\[60^\circ \].
\[90^\circ \].
Hình bình hành \(ABCD\) là hình chữ nhật khi
\[AB = AD\].
\[\widehat A = 90^\circ \].
\[AB = 2AC\].
\[\widehat A = \widehat C\].
Để chứng minh tứ giác \(ABCD\) là hình vuông, dấu hiệu nào sau đây là sai?
Tứ giác \(ABCD\) là hình thoi có hai đường chéo bằng nhau.
Tứ giác \(ABCD\) là hình thoi có một góc vuông.
Tứ giác \(ABCD\) là hình thoi có hai đường chéo vuông góc.
Tứ giác \(ABCD\) là hình chữ nhật có hai cạnh kề bằng nhau.








