Đề cương ôn tập giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới (Tự luận) có đáp án - Phần 2

Một cửa hàng bán quần áo có chương trình khuyến mãu như sau: Khách hàng có thẻ thành viên sẽ được giảm \(15\% \) tổng số tiền của hóa đơn. Bạn Bình có thẻ thành viên, bạn mua hai chiếc sơ mi, mỗi áo đều có giá \(200{\rm{ 000}}\) đồng và một quần Jeans với giá \(350{\rm{ 000}}\). Bạn Bình đưa cho người thu ngân 1 triệu đồng. Hỏi bạn Bình được trả lại bao nhiêu tiền?

Sau những vụ va chạm giữa các xe trên đường, cảnh sát thường sử dụng công thức dưới đây để ước lượng tốc độ \(v\) (đơn vị: dặm/giờ) của xe từ vế trượt trên mặt đường sau khi phanh đột ngột:

\(v = \sqrt {30fdn} \),

trong đó, \(d\) là chiều dài vết trượt của bánh xe trên nền đường tính bằng feet (ft), \(f\) là hệ số ma sát giữa bánh xe và mặt đường (là thước đo sự “trơn trượt” của mặt đường), \(n\) là mức độ hiệu quả của phanh.

Bác Minh điều khiển xe chạy trên một đoạn cao tốc có tốc độ giới hạn là \(100\) km/giờ. Để tránh một xe dừng khẩn cấp phía trước, bác Minh đã phanh xe của mình lại. Khi đến hiện trường, cảnh sát đo được vết trượt xe của bác Minh là \(d = 152{\rm{ ft}}\). Bác Minh khẳng định mình đi đúng với tốc độ giới hạn. Em hãy giúp chú cảnh sát kiểm tra xem bác Minh nói đúng hay sai? Biết rằng hệ số ma sát của mặt đường tại thời điểm đó là \(f = 0,7\) và mức độ hiệu quả của phanh là \(n = 100\% \). (Biết 1 dặm = 1609 m).

Một cửa hàng nhập một lô gồm 100 máy tính Casio với giá nhập là \(480{\rm{ 000}}\) đồng một sản phẩm. Sau đó khi bán 70 chiếc với tiền lãi bằng \(30\% \) giá nhập, cửa hàng bán số máy còn lại với giá bằng \(70\% \) giá bán trước đó. Hỏi sau khi bán hết lô hàng thì cửa hành lãi hay lỗ bao nhiêu tiền?

Nhân dịp khai trương, một cửa hàng bánh Pizza giảm giá 10% tất cả các sản phẩm và giảm thêm 5% trên giá đã giảm khi mua từ hai sản phẩm trở lên. Bác Lan mua một Pizza rau củ size vừa giá \(129{\rm{ 000}}\) đồng và một Pizza thập cẩm size lớn giá \(249{\rm{ 000}}\) đồng. Hỏi nếu bác Lan đưa cho nhân viên thu ngân \(500{\rm{ 000}}\) đồng thì bác được trả lại bao nhiêu tiền?

Nhiệt độ ngoài trời đo được vào một ngày mùa đông tại New York (Mỹ) lúc 5 giờ chiều là \(35,6^\circ {\rm{F}}\) lúc 10 giờ tối cùng ngày là \(22,64^\circ {\rm{F}}\). Biết công thức chuyển từ độ F sang độ C là:

\({\rm{T}}\left( {{\rm{^\circ C}}} \right) = \frac{5}{9} \cdot \left( {{\rm{T}}\left( {{\rm{^\circ F}}} \right) - 32} \right)\),

a) Hãy chuyển đổi các số đo nhiệt độ từ độ F được nêu trên sang độ C.

b) Tính độ chênh lệch nhiệt độ từ 5 giờ chiều đến 10 giờ tối (theo đơn vị độ C).

Một nhà mạng cung cấp các gói mạng 4G theo tháng cho khách hàng. Trong đó, có hai gói phổ biến như sau:

− Gói cố định: Mức giá là \(285{\rm{ }}000\) đồng/tháng, không giới hạn data sử dụng.

− Gói linh hoạt: Mức giá là \(160{\rm{ 000}}\) đồng/tháng, cho phép khách hàng sử dụng 4Gb/ngày. Nếu vượt quá số data này, người dùng sẽ trả thêm \(5{\rm{ }}000\) đồng cho mỗi Gb vượt.

Giả sử mỗi tháng có 30 ngày, trung bình mỗi tháng anh Hải sử dụng 150Gb. Hỏi anh Hải nên đăng kí theo hình thức nào tiết kiệm hơn? Và tiết kiệm được bao nhiêu tiền mỗi tháng?

Cho hình vẽ bên.

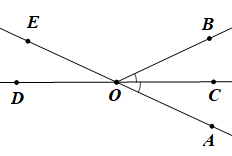
Biết \(\widehat {AOB} = 50^\circ \), tia \(OC\) là tia phân giác của góc \(AOB\).

a) Vẽ lại hình và kể tên góc kề bù với góc \(AOC.\)

b) Tính số đo của mỗi góc \(BOE,\,\,AOD\).

Cho hình vẽ bên.

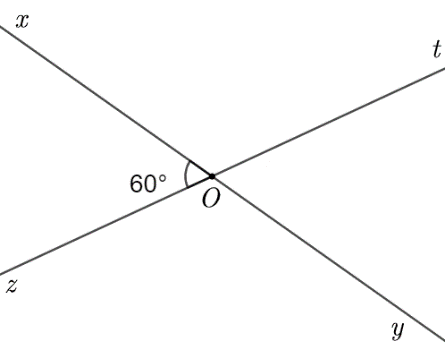
a) Kể tên các cặp góc đối đỉnh trong hình.

b) Vẽ \(Om\) là tia phân giác của góc \(\widehat {xOz}\). Tính số đo góc \[\widehat {tOy};\,\,\widehat {xOt};\]\(\widehat {mOx}\).

Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 80^\circ \). Trên mặt phẳng bờ \(Ox\) chứa tia \(Oz\) vẽ tia \(Ot\) sao cho \[\widehat {xOt} = 160^\circ \]. Chứng tỏ \(Oz\) là tia phân giác của \(\widehat {xOt}\).

Cho hai đường thẳng \(a\) và \(b\) song song với nhau. Trên đường thẳng \(a\) lấy hai điểm \(A\) và \(E\) (điểm \(A\) không trùng với điểm \(E\)). Kẻ \(AB\) vuông góc với đường thẳng \(b\) tại \(B\). Lấy điểm \(D\) thuộc đường thẳng \(b\) sao cho \(\widehat {AED} = 65^\circ .\)

a) Vẽ hình và viết giả thiết, kết luận của bài toán.

b) Tính số đo của \(\widehat {BAE}\) và \(\widehat {BDE}\).

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:

a) \(\frac{5}{{n - 2}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:b) \(\frac{{ - 6}}{{n + 1}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:

c) \(\frac{{ - 3}}{{n - 4}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:d) \(\frac{{6n - 4}}{{2n + 1}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:e) \(\frac{{3n + 2}}{{4n - 5}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:

g) \(\frac{{4n - 1}}{{3 - 2n}}\).

Tìm giá trị nhỏ nhất của biểu thức:

a) \[{\left( {2x - 3} \right)^2} + 15\];

Tìm giá trị nhỏ nhất của biểu thức:

b) \({\left( {5x + 7} \right)^8} - 2020\);

Tìm giá trị nhỏ nhất của biểu thức:

c) \(2016 + \left| {1 - 2019x} \right|\);

Tìm giá trị nhỏ nhất của biểu thức:d) \( - 9 + \left| {4x + 1} \right|\);

Tìm giá trị nhỏ nhất của biểu thức:e) \(\left| {x - 1} \right| + \left| {x - 2} \right|\);

Tìm giá trị nhỏ nhất của biểu thức:

g) \(2021 - \frac{{15}}{{3 + \left| {x - 2021} \right|}}\).

Tìm giá trị lớn nhất của biểu thức:

a) \[8 - {\left( {4x - 7} \right)^2}\];        

Tìm giá trị lớn nhất của biểu thức:b) \(7 - \left| {6x - 1} \right|\);

Tìm giá trị lớn nhất của biểu thức:

c) \(6 - \left| {{x^2} + 5} \right|\);

Tìm giá trị lớn nhất của biểu thức:d) \(14 + \frac{3}{{2 + {{\left( {5x - 6} \right)}^2}}}\);

Tìm giá trị lớn nhất của biểu thức:e) \( - 6 + \frac{{15}}{{5 + \left| {7x + 4} \right|}}\);   

Tìm giá trị lớn nhất của biểu thức:

g) \(\frac{{4{x^2} + 9}}{{{x^2} + 1}}\).

Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{14 - x}}{{4 - x}}\] với mọi \(x \in \mathbb{Z}\). Khi đó \[x\] nhận giá trị nguyên nào?