Đề cương ôn tập cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới (Tự luận) có đáp án - Phần 2

Tìm \(x\), biết:

h) \( - 1 + \left| {x + 4,5} \right| = - 6,2\).

Tìm \(x\), biết:g) \(0,2 + \left| {x - 2,3} \right| = 1,1\);

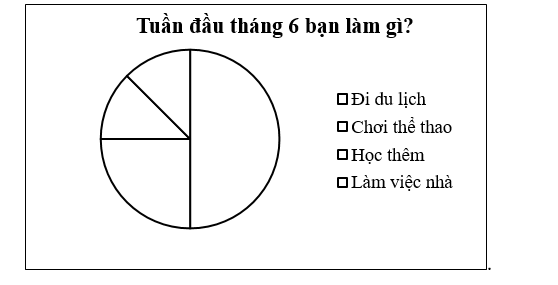
An đã hỏi một số bạn trong trường về hoạt động chiếm nhiều thời gian nhất trong tuần đầu tháng 6 vừa qua và thu được dữ liệu sau (D: Đi du lịch, C: Chơi thể thao, H: Học thêm, L: Làm việc nhà).

a) An đã dùng phương pháp thu thập dữ liệu nào: quan sát, làm thí nghiệm, lập bảng hay hỏi phỏng vấn.

b) Dữ liệu thu được thuộc loại nào?

c) Hoàn thiện bảng thống kê sau vào vở.

d) Hoàn thiện biểu đồ hình quạt tròn vào vở.

Minh làm bài kiểm tra trình độ tiếng Anh trên mạng Internet 6 lần và ghi lại kết quả (tỉ lệ số Câu đúng) như sau:

a) Vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên.

b) Nhận xét về sự tiến bộ của Minh sau mỗi lần làm bài.

Nhà trường vận động mỗi bạn tặng một món quà cho các bạn học sinh vùng lũ lụt. Biểu đồ sau đây biểu diễn tỉ lệ học sinh lớp 7A tặng các món quà khác nhau.

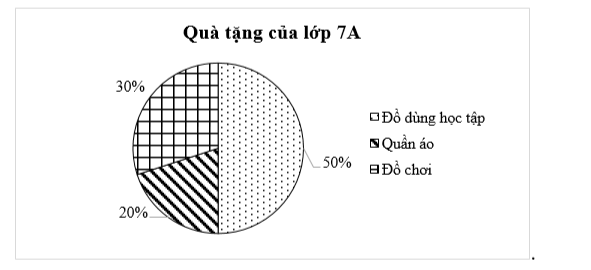
a) Từ biểu đồ, em hãy lập bảng thống kê về tỉ lệ học sinh lớp 7A tặng các món quà khác nhau.

b) Lớp 7A có 40 học sinh. Tính số họ sinh tặng từng loại món quà.

Một nghiên cứu đã đưa ra tỉ lệ học sinh cấp THCS nghiện điện thoại di động trong những năm gần đây như biểu đồ dưới:

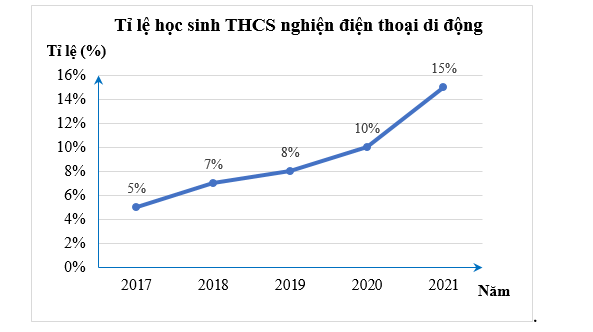
a) Từ biểu đồ, em hãy lập bảng thống kê về tỉ lệ học sinh cấp THCS nghiện điện thoại di động trong những năm gần đây.

b) Trục đứng biểu diễn đại lượng gì? Dữ liệu về đại lượng này thuộc loại nào?

c) Năm 2021, một trường THCS có 1000 học sinh. Hãy ước lượng số học sinh nghiện điện thoại di động của trường?

Kết quả tìm hiểu về lựa chọn các hoạt động thể thao trong hè của các bạn học sinh lớp 7E được cho bởi bảng thống kê sau:

a) Hãy phân loại các dữ liệu có trong bảng thống kê trên.

b) Lớp 7E có bao nhiêu học sinh?

Điều tra về cân nặng (kg) của 30 bạn học sinh lớp 7A, giáo viên ghi lại trong bảng sau:

a) Hoàn thành bảng số liệu thống kê cân nặng của 30 bạn học sinh lớp 7A theo mẫu sau:

b) Vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu trên.

Kết quả điều tra về sự yêu thích các môn học của 300 học sinh lớp 7 được cho dưới dạng biểu đồ quạt bên dưới:

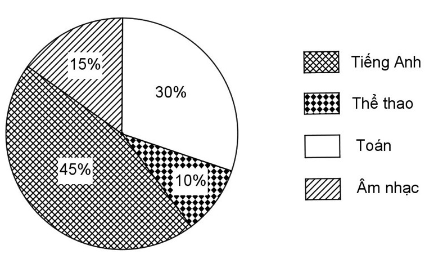
Em hãy cho biết:

a) Có bao nhiêu học sinh thích môn Toán?

b) Số học sinh yêu thích môn Âm Nhạc hay môn Thể thao nhiêu hơn và nhiều hơn bao nhiêu học sinh?

Biểu đồ dưới đây cho biết tỉ lệ các loại hoa nhập về của cửa hàng A trong một ngày

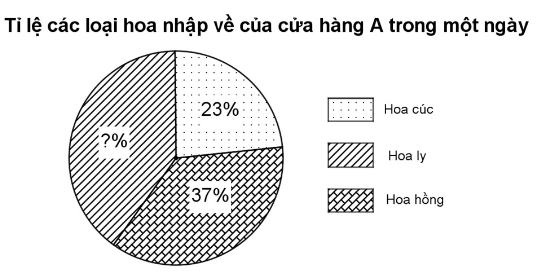
a) Tính tỉ lệ phần trăm của hoa ly nhập về trong cửa hàng và vẽ bảng thống kê biểu diễn biểu đồ trên.

b) Biết một ngày cửa hàng A nhập tổng cộng 2000 bông. Tính số lượng hoa nhập về mỗi loại trong một ngày của cửa hàng A.

Biểu đồ bên biểu diễn số trận đấu của cầu thủ Quang Hải trong giải Vô địch bóng đá Quốc gia Việt Nam.

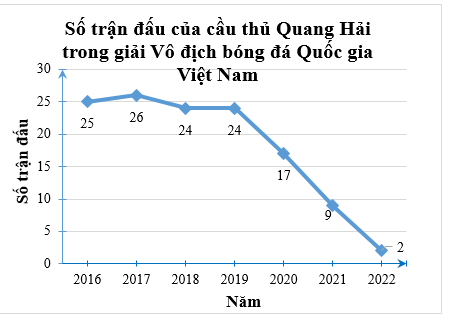
a) Mùa giải năm 2017, Quang Hải thi đấu bao nhiêu trận trong giải Vô địch Quốc gia Việt Nam?

b) Quang Hải thi đấu tổng cộng bao nhiêu trận cho giải Vô địch Quốc gia Việt Nam trong 7 mùa giải?

c) Số trận đấu của Quang Hải trong giải Vô địch Quốc gia Việt Nam năm 2022 giảm bao nhiêu phần trăm so với năm 2021 (kết quả làm tròn đến hàng phần trăm)?

Biểu đồ hình quạt sau đây biểu diễn kết quả đánh giá xếp loại học sinh cuối học kì I của học sinh khối 7. Quan sát các dữ liệu trên biểu đồ và trả lời các câu hỏi sau đây:

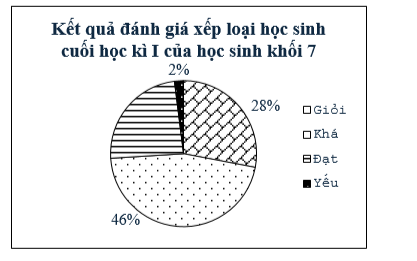
a) Tỉ lệ học sinh xếp loại Đạt của khối 7.

b) Số học sinh xếp loại Giỏi gấp bao nhiêu lần số học sinh xếp loại Yếu?

c) Tổng số học sinh xếp loại Khá, Giỏi chiếm bao nhiêu phần trăm tổng số học sinh khối 7?

d) Biết khối 7 có 350 học sinh. Tính số học sinh xếp loại Giỏi của khối 7.

Bác Hoa gửi ngân hàng A số tiền 70 triệu đồng với kỳ hạn 1 năm lãi suất \(5,6\% \)/năm. Bác Hoa gửi ngân hàng B số tiền 50 triệu đồng với kỳ hạn 1 năm lãi suất \(6,5\% \)/năm.

a) Sau một năm, số tiền cả gốc lần lãi mà bác Hoa thu được là bao nhiêu?

b) Giả sử sau khi hết năm đầu, lãi suất của ngân hàng A giảm còn \(5,5\% \)/năm, ngân hàng B tăng lãi suất lên \(6,8\% \)/năm. Vì vậy bác Hoa rút 60% số tiền ở ngân hàng A và gửi tiếp vào ngân hàng B. Hỏi hết năm thứ hai thì số tiền cả gốc và lãi mà bác Hoa thu được là bao nhiêu?

Bạn Na muốn tạo một trang web để kết bạn. Trang web nhận được 3 lần truy cập trong tuần đầu tiên. Nếu lượng truy cập tăng lên gấp 3 lần sau mỗi tuần tiếp theo thì tới tuần thứ 6 trang web của Na có tất cả bao nhiêu lượt truy cập?

Sự sinh trưởng của vi sinh vật là sự tăng lên về số lượng và chủng loại theo thời gian. Thời gian thế hệ là thời gian cần thiết cho một tế bào phân chia (hay quần thể nhân đôi) về mặt số lượng cá thể. Biết rằng E.coli có thời gian thế hệ là 20 phút (cứ 20 phút nhân đôi một lần). Hãy tính số lượng E.coli sau 3 giờ 40 phút.

Chủ cửa hàng bỏ ra \(40\) triệu đồng mua một loại sản phẩm để bán. Chủ nhân cửa hàng đã bán \(\frac{7}{8}\) số sản phẩm mua về với giá cao hơn \(10\% \) so với giá mua vào và bán \(\frac{1}{8}\) số sản phẩm còn lại với giá bán mỗi sản phẩm thấp hơn \(20\% \) so với giá mua vào. Tính số tiền chủ cửa hàng thu về được khi bán hết số hàng. Cửa hàng đã lãi hay lỗ bao nhiêu phần trăm?

Sân nhà Lan có dạng hình vuông được lát bằng 441 viên gạch. Các viên gạch được lát đều có dạng hình vuông và có cùng kích thước. Hai đường chéo của sân được lát bằng các viên gạch màu trắng, phần còn lại được lát bằng các viên gạch màu đỏ. Biết giá tiền một viên gạch đỏ là 30 nghìn đồng, giá tiền một viên gạch trắng bằng \(\frac{{11}}{{10}}\) giá tiền một viên gạch màu đỏ.

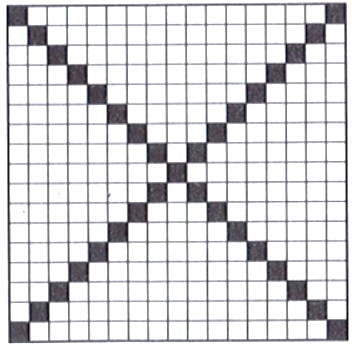
Hỏi nhà Lan mua gạch để lát sân hết bao nhiêu tiền?

Cho hình vẽ bên có \[\widehat {xOM} = \widehat {yON} = 30^\circ ,\,\,OI\] là tia phân giác của góc \[MON\]. Hai đường thẳng \[OI,xy\] có vuông góc với nhau hay không?

Cho đường thẳng \[xx'\] cắt \[yy'\] tại \[A\].

a) Kể tên các cặp góc đối đỉnh;

b) Kể tên các cặp góc kề bù;

c) Dùng dụng cụ học tập để vẽ tia phân giác của góc \[xAy\].

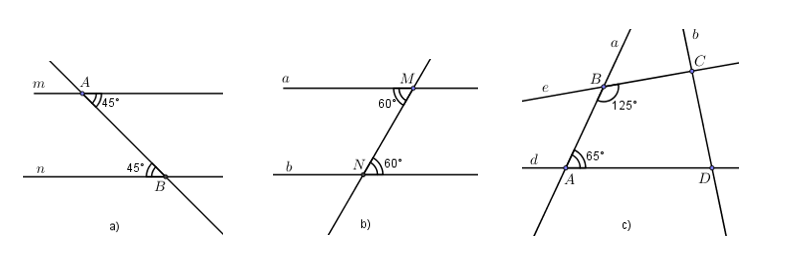
Cho các hình vẽ sau, hãy cho biết những cặp đường thẳng nào song song với nhau và giải thích vì sao?

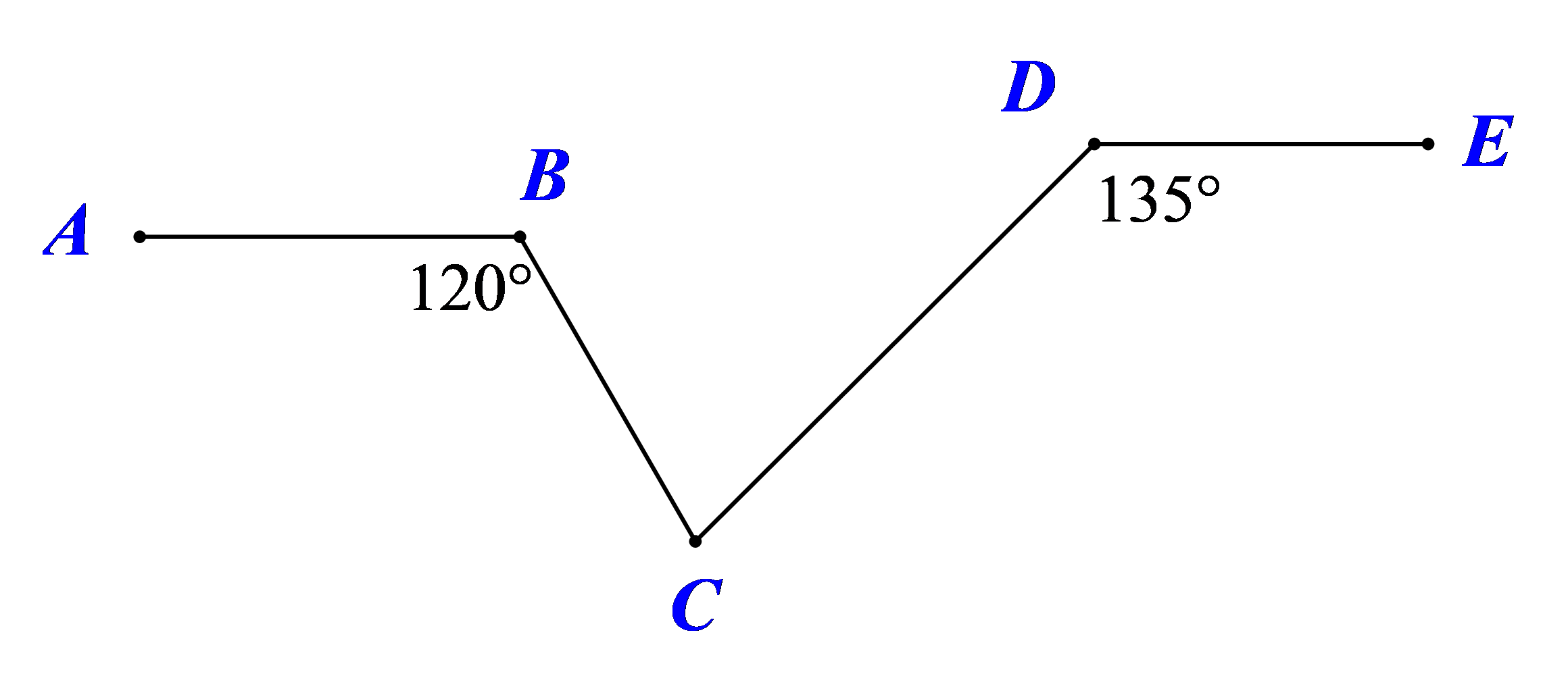
Cho hình vẽ \(AB\,{\rm{//}}\,DE\). Tính số đo \(\widehat {BCD}\).

Cho hình vẽ sau.

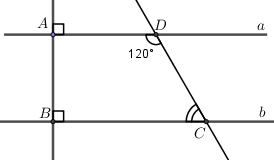
a) Chứng minh \(a\parallel b\).

b) Tính số đo góc \(C\).

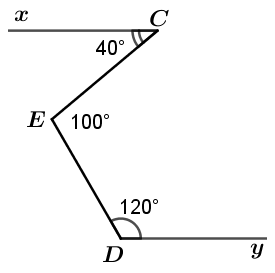
Cho hình vẽ bên, biết \(\widehat C = 40^\circ ,\widehat D = 120^\circ ,\widehat E = 100^\circ \). Chứng tỏ \(Cx\parallel Dy\).

Cho hình vẽ bên biết thanh gỗ \(AB\)dựa vào tường làm thành góc \(63^\circ \) so với mặt đất, người ta dùng tiếp thanh gỗ \(CD\) đặt vuông góc với tường sao cho điểm \(D\)nằm trên thanh gỗ \(AB\). Hãytính góc tạo bởi thanh gỗ \(CD\) và thanh gỗ \(AB\).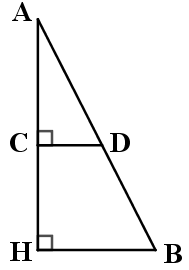

Cho tam giác \[ABC\] nhọn. Gọi \[M\] là trung điểm của \[AC\]. Trên tia đối của tia \[MB\]lấy điểm \[D\] sao cho \[MD = MB\].

a) Chứng minh \[\Delta AMB = \Delta CMD\].

b) Chứng minh \[AD\parallel BC\].

c) Kẻ \[{\rm{MH}} \bot {\rm{AB}}\] và \[{\rm{MK}} \bot {\rm{DC}}\]. Chứng minh \[{\rm{M}}\] là trung điểm của \[{\rm{HK}}\].

Cho tam giác \(ABC\) có \(AB < AC\). Kẻ tia phân giác \(AD\) của góc \(BAC\) (\(D\) thuộc cạnh \(BC\)). Trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AE = AB\), trên tia \(AB\) lấy điểm \(F\) sao cho \(AF = AC\). Chứng minh rằng:

a) \[\Delta BDF = \Delta EDC\].

b) điểm \(F,\,D,\,E\) thẳng hàng

c) \(AD\) là đường trung trực của \(BE\) và \(CF\).

Cho \(\Delta ABC\) vuông tại \(A\)\(\left( {AB > AC} \right)\) tại \(C\). Tia phân giác góc \(ACB\) cắt cạnh \(AB\) tại \(D.\) Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(CE = CA\).

a) Chứng minh \(DE \bot BC\).

b) Vẽ đường thẳng \(d\) vuông góc với \(AC\) tại \(C\). Qua \(A\) vẽ đường thẳng song song với \(CD\) cắt \(d\) tại \(M\). Chứng minh \(AM = CD\).

c) Qua \(B\) vẽ đường thẳng vuông góc với \(CD\) tại \(N\) cắt \(AC\) tại \(K\). Chứng minh \(KE \bot BC\) và ba điểm \(K,\,D,\,E\) thẳng hàng.

Cho \(\Delta ABC\) có \(AB < AC.\) Kẻ \(AH\) vuông góc với \(BC\,\,\left( {H \in BC} \right)\). Trên tia \(AH\) lấy điểm \(K\) sao cho \(H\) là trung điểm của \(AK\).

a) chứng minh: \(\Delta AHC = \Delta KCH\).

b) Gọi \(E\) là trung điểm của \(BC\). Trên tia \(AE\) lấy điểm \(D\)sao cho \(E\) là trung điểm của \(AD\). Chứng minh rằng: \(BD = AC = CK\).

c) chứng minh rằng: \(EH\) là tia phân giác của góc \(\widehat {AEK}\) và \(DK{\rm{//}}BC\).

d) Gọi \(I\) là giao điểm của \(BD\) và \(CK\), \(N\) là trung điểm của \(KD\). Chứng minh: \(E,I,N\) thẳng hàng.

Cho \[\Delta ABC\] có \[AB = AC\], \[M\] là trung điểm của \[BC\]. Trên tia đối của tia \[MA\] lấy điểm \[D\] sao cho \[AM = MD\].

a) Chứng minh rằng \(\Delta ABM = \Delta DCM\).

b) Chứng minh \(AB\parallel DC\).

c) Chứng minh \(AM \bot BC\).

d) Tìm điều kiện của \(\Delta ABC\) để góc \(\widehat {ADC} = 45^\circ \).