Đề cương ôn tập giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới (Trắc nghiệm) có đáp án
36 câu hỏi
Cách biểu diễn số \(\frac{5}{3}\) trên trục số nào dưới đây là đúng?
A.  ;
;
B. 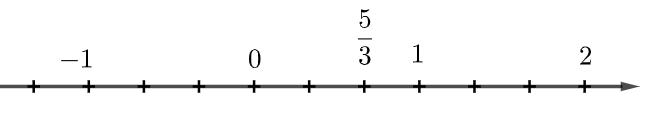 ;
;
C.  ;
;
D.  .
.
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với
\[a,\,\,b \in \mathbb{N};\,\,a \ne 0\].
\[a,\,\,b \in \mathbb{N};\,\,b \ne 0\].
\[a,\,\,b \in \mathbb{Z};\,\,b \ne 0\].
\[a = 0;\,\,b \ne 0\].
Trong các số sau đây, số nào biểu diễn số hữu tỉ \(\frac{{ - 2}}{3}\)?
\(\frac{4}{6}\).
\(\frac{{ - 6}}{9}\).
\(\frac{{ - 4}}{9}\).
\(\frac{{ - 4}}{{ - 6}}\).
Đối với biểu thức có chứa dấu ngoặc thì thứ tự thực hiện phép tính trên tập số hữu tỉ nào dưới đây là đúng?
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\).
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\).
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\).
\(\left( {} \right) \to \left\{ {} \right\} \to \left[ {} \right]\).
Cho trục số.

Điểm \(B\) trên trục số biểu diễn số hữu tỉ nào?
\(\frac{7}{5}\).
\(\frac{{ - 2}}{5}\).
\(\frac{9}{5}\).
\(\frac{3}{5}\).
Khẳng định nào sau đây là đúng?
\(0,125 \in \mathbb{Q}\).
\( - 10 \in \mathbb{N}\).
\(5\frac{1}{3} \notin \mathbb{Q}\).
\(3 \notin \mathbb{Z}\).
Số đối của số \( - \frac{{ - 3}}{5}\) là
\(\frac{5}{3}\).
\( - \frac{5}{3}\).
\( - \frac{3}{5}\).
\(\frac{3}{5}\).
Số đối của số hữu tỉ \[ - \frac{1}{4}\] là
\[4\].
\[ - 4\].
\(\frac{{ - 1}}{4}\).
\(\frac{1}{4}\).
Điền dấu thích hợp vào chỗ chấm \(3,25.... - 3\frac{4}{7}\) là
\( \le \).
=.
<.
>.
Các số \( - 2,15\,;\,\,\frac{5}{4};\,\, - 3\frac{1}{5};\,\,2\,;\,\,0\) được sắp xếp theo thứ tự giảm dần là
\[2;\,\,\frac{5}{4};\,\,0;\,\, - 2,15;\,\, - 3\frac{1}{5}\].
\[0;\,\,\frac{5}{4};\,\,2;\,\, - 2,15;\,\, - 3\frac{1}{5}\].
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,\frac{5}{4};\,\,2\).
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,2;\,\,\frac{5}{4}\).
Kết quả làm tròn đến chữ số thập phân thứ tư của \[\sqrt {17} \]là
\[4,1232\].
\[4,1231\].
\[4,1230\].
\[4,1233\].
Trong các số thập phân sau, số nào là số thập phân hữu hạn?
\[ - 5,348\].
\[ - 5,348...\].
\[ - 5,3\left( {48} \right)\].
\[ - 5,\left( {348} \right)\].
Trong các khẳng định sau, khẳng định nào đúng?
\[\sqrt {13} \in \mathbb{Q}\].
\[1,\left( 3 \right) \in \mathbb{N}\].
\[ - 3,456 \in \mathbb{Z}\].
\[\sqrt 5 \in \mathbb{R}\].
Kết quả của phép tính \(\frac{{{{20}^5}\,\,.\,\,{5^{10}}}}{{{{100}^5}}}\) là
3125.
1.
1225.
1525.
Trong các khẳng định sau, khẳng định nào đúng?
\[\frac{{ - 1}}{3} < - 0,5\].
\[\sqrt {\frac{{16}}{{25}}} = \frac{4}{5}\].
\[\sqrt {\frac{4}{9}} < \frac{1}{3}\].
\[1,2\left( 3 \right) = 1,23\].
Giá trị của\[x\] thỏa mãn \[\left| x \right| = 1,2\] là
\[x = - 1,2\].
\[x = 1,2\].
\[x \in \left\{ {1,2\,;\, - 1,2} \right\}\].
\[x = - \left( { - 1,2} \right)\].
Số nào sau đây là số thập phân vô hạn tuần hoàn?
\[1,25\].
\(\sqrt 5 \).
\[2,3\left( 4 \right)\].
\(\frac{{ - 3}}{4}\).
Trong các khẳng định sau, khẳng định nào là đúng?
Số vô tỉ không phải là số thập phân vô hạn không tuần hoàn;
Số vô tỉ là số được viết được dưới dạng số thập phân vô hạn không tuần hoàn;
Số vô tỉ cũng là số thập phân hữu hạn;
Số vô tỉ là số thập phân vô hạn tuần hoàn.
Giá trị tuyệt đối của \( - \sqrt 5 \) là
\( - \sqrt 5 \).
\(\frac{{ - 1}}{{\sqrt 5 }}\).
\(\frac{1}{{\sqrt 5 }}\).
\(\sqrt 5 \).
Trên trục số nằm ngang, điểm \(A\) và \(B\) lần lượt biểu biễn hai số thực \(\frac{{ - 1}}{2}\) và \(\sqrt 2 \) thì
Điểm \(A\) nằm bên trái điểm \(B\).
Điểm \(A\) nằm bên phải điểm \(B\).
Điểm \(A\) nằm phía dưới điểm \(B\).
Điểm \(A\) nằm phía trên điểm \(B\).
Hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\). Góc đối đỉnh với \[\widehat {yOx'}\] là
\[\widehat {y'Ox'}\].
\[\widehat {y'Ox}\].
\[\widehat {yOx'}\].
\[\widehat {yOx}\].
Cho hai đường thẳng \(ab\) và \(cd\) cắt nhau tại \(O\) sao cho \(\widehat {aOc} = 120^\circ \). Khẳng định nào dưới đây làđúng?
\[\widehat {bOd} = 60^\circ \].
\[\widehat {bOc} = 60^\circ \].
\[\widehat {aOd} = 120^\circ \].
\[\widehat {bOc} = 120^\circ \].
Cho \(\widehat {mOn} = 110^\circ \), tia \(Ot\) là tia phân giác của \(\widehat {mOn}\). Khi đó, số đo \(\widehat {mOt}\) là
\[55^\circ \].
\[110^\circ \].
\[60^\circ \].
Một giá trị khác.
Hai góc kề bù có tổng số đo bằng bao nhiêu?
\[90^\circ \].
\[180^\circ \].
\[45^\circ \].
\[30^\circ \].
Cho các bước vẽ tia phân giác \(Ot\)của \(\widehat {xOy} = 110^\circ \) bằng thước đo góc như sau:
(1).Đặt thước đo góc sao cho tâm của thước trùng với điểm \(O\)của tia \(Ox\) và tia \(Ox\) đi qua vạch \(0^\circ .\)Vẽ tia \(Oy\) đi qua vạch \(110^\circ \) của thước. Ta vẽ được \(\widehat {yOx} = 110^\circ \).
(2). Vì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên ta có \(\widehat {xOt} = \widehat {tOy} = \frac{{\widehat {xOy}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \). Do đó, đặt thước đo góc sao cho tâm của thước trùng với điểm \(O\) của tia \(Ox\) và tia \(Ox\) đi qua vạch \(0^\circ .\)Vẽ tia \(Ot\) đi qua vạch \(55^\circ \) và tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\), ta được tia phân giác \(Ot\) của \(\widehat {xOy}.\)
(3). Vẽ tia \(Ox.\)
Sắp xếp các bước trên để có thứ tự đúng các bước vẽ tia phân giác \(Ot\)của \(\widehat {xOy} = 110^\circ \) bằng thước đo góc là
(3) → (2) → (1).
(1) → (2) → (3).
(2) → (1) → (3).
(3) → (1) → (2).
Cho \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) là hai góc đối đỉnh. Biết \(\widehat {x'Oy'} = 45^\circ \) ta suy ra được góc \(xOy\) là
Góc nhọn;
Góc vuông;
Góc tù;
Góc bẹt.
Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]?
A. ![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1758522082.png)
B. ![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1758522105.png)
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/09/16-1758522120.png)
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/09/17-1758522136.png)
Các cặp góc đối đỉnh trong hình bên là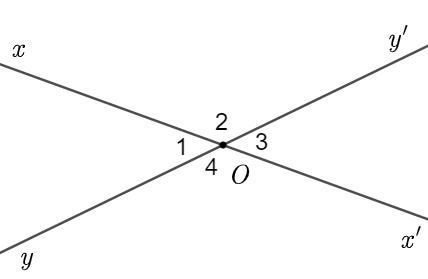
\({\widehat O_1}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_3}\).
\({\widehat O_1}\) và \({\widehat O_2}\); \({\widehat O_3}\) và \({\widehat O_4}\).
\({\widehat O_2}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_4}\).
\({\widehat O_1}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_4}\).
Cho hình vẽ, biết \[m\,{\rm{//}}\,n\]. Trong các khẳng định sau, khẳng định nào sai?

\[\widehat {{P_1}} = \widehat {{Q_1}}\].
\[\widehat {{P_1}} + \widehat {{Q_2}} = 180^\circ \].
\[\widehat {{P_2}} = \widehat {{Q_1}}\].
\[\widehat {{P_1}} = \widehat {{P_2}}\].
Cho hình vẽ dưới đây biết \[a\,\parallel b\]và \[\widehat {{M_1}} = 45^\circ .\] Khi đó, số đo\[\widehat {{N_1}}\] là ![Cho hình vẽ dưới đây biết \[a\,\parallel b\] và \[\widehat {{M_1}} = 45^\circ .\] Khi đó, số đo \[\widehat {{N_1}}\] là A. \[45^\circ \]. B. \[35^\circ \]. C. \[135^\circ \]. D. \[115^\circ \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/46-1758522326.png)
\[45^\circ \].
\[35^\circ \].
\[135^\circ \].
\[115^\circ \].
Cho hình vẽ biết \[MN\parallel EF\], khi đó khẳng định nào sau đây là đúng? ![Cho hình vẽ biết \[MN\parallel EF\], khi đó khẳng định nào sau đây là đúng? A. \(x = y\). B. \(x = y - 180^\circ \). C. \(x = 180^\circ + y\). D. \(x + y = 180^\circ \). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/47-1758522371.png)
\(x = y\).
\(x = y - 180^\circ \).
\(x = 180^\circ + y\).
\(x + y = 180^\circ \).
Tìm số đo góc \(x\) trong hình vẽ bên là ![Tìm số đo góc \(x\) trong hình vẽ bên là A. \[135^\circ \]. B. \[45^\circ \]. C. \[90^\circ \]. D. Kết quả khác. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/48-1758522428.png)
\[135^\circ \].
\[45^\circ \].
\[90^\circ \].
Kết quả khác.
Chứng minh định lí là
Dùng hình vẽ để từ giả thiết suy ra kết luận.
Dùng đo đạc thực tế để suy ra kết luận từ giả thiết.
Dùng lập luận để từ giả thiết suy ra kết luận.
Cả A, B, C đều sai.
Trong các khẳng định sau, khẳng định nào là định lí?
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng vuông góc với nhau.
Một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì bằng nhau.
Cho định lí: “Hai góc đối đỉnh thì bằng nhau” và hình vẽ minh hoạ sau:
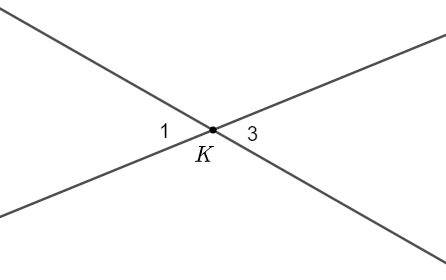
Viết giả thiết, kết luận cho định lí trên:
GT | \({\widehat K_1}\) và \({\widehat K_3}\) là hai góc đối đỉnh |
KL | \({\widehat K_1} + {\widehat K_3} = 180^\circ \) |
GT | \({\widehat K_1}\) và \({\widehat K_3}\) là hai góc bù nhau |
KL | \({\widehat K_1} + {\widehat K_3} = 180^\circ \) |
GT | \({\widehat K_1}\) và \({\widehat K_3}\) là hai góc đối đỉnh |
KL | \({\widehat K_1} = {\widehat K_3}\) |
GT | \({\widehat K_1}\) và \({\widehat K_3}\) là hai góc kề bù |
KL | \({\widehat K_3} = {\widehat K_4}\) |
Trong những câu dưới đây, câu nào không phải là định lí?
Hai góc đối đỉnh thì bằng nhau.
Hai góc kề nhau thì có tổng số đo là \[180^\circ \].
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Đường thẳng vuông góc với một trong hai đường thẳng song song thì đường thẳng đó vuông góc với đường thẳng còn lại.