Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 6
5 câu hỏi
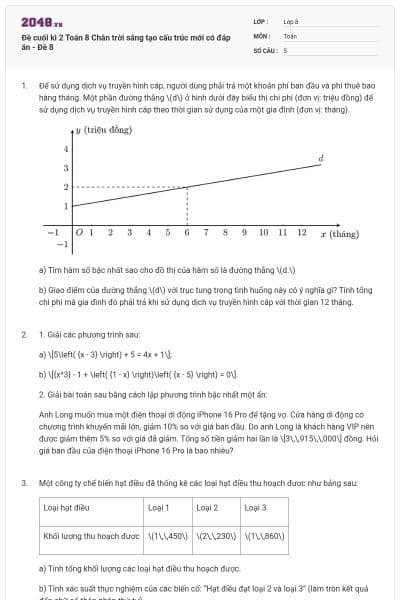
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất \(y = ax + b,\) trong đó \(b\) biểu thị chi phí cố định của hoạt động kinh doanh và hệ số \(a\) biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là \(1,8\) triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí \(y\) (triệu đồng) để sản xuất \(x\) (xe đạp) trong một ngày.
b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?
1. Giải các phương trình sau:
a) \[7x - 10 = 4x + 11\];
b) \[x{\left( {x + 3} \right)^2} - 3x = {\left( {x + 2} \right)^3} + 1\].
2. Giải bài toán sau bằng cách lập phương trình bậc nhất một ẩn:
Tại điểm tiêm phòng Covid-19 trường A, một bàn tiêm dự định tiêm một số mũi tiêm vaccine phòng Covid-19 cho người dân trong 20 ngày. Do yêu cầu cấp bách của việc phòng bệnh, bàn tiêm đã tăng năng suất thêm 20% nên sau 18 ngày không những đã tiêm xong số mũi tiêm dự định mà còn tiêm thêm được 24 mũi tiêm nữa. Tính số mũi tiêm phòng Covid-19 mà một bàn tiêm dự định tiêm.
Bạn An gieo xúc xắc 80 lần. Bạn An đếm được có 13 lần xuất hiện mặt 2 chấm, 12 lần xuất hiện mặt 4 chấm và 14 lần xuất hiện mặt 6 chấm.
a) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số 4”.
b) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ”.
c) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” với xác suất của biến cố đó khi số lần gieo ngày càng lớn.
1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái \[PQ = 1,5\,\,{\rm{m}}.\] Chú thợ nhẩm tính chiều dài mái \[DE\] biết \[Q\] là trung điểm \[EC,{\rm{ }}P\] là trung điểm của \[DC.\] Tính giúp chú thợ xem chiều dài mái \[DE\] bằng bao nhiêu (xem hình vẽ minh họa)?
![1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái \[PQ = 1,5\,\,{\rm{m}}.\] Chú thợ nhẩm tính chiều dài mái \[DE\] biết \[Q\] là trung điểm \[EC,{\rm{ }}P\] là trung điểm của \[DC.\] Tính giúp chú thợ xem chiều dài mái \[DE\] bằng bao nhiêu (xem hình vẽ minh họa)? 2. Cho tam giác \[ABC\] nhọn \[\left( {AB < AC} \right)\] có hai đường cao \[BE,{\rm{ }}CF\] cắt nhau tại \[H.\] a) Chứng minh: . b) Chứng minh: \(AF \cdot AB = AE \cdot AC\). c) Đường thẳng qua \[B\] và song song với \[EF\] cắt \[AC\] tại \[M.\] Gọi \[I\] là trung điểm của \[BM,{\rm{ }}D\] là giao điểm của \[EI\] và \[BC.\] Chứng minh ba điểm \[A,{\rm{ }}H,{\rm{ }}D\] thẳng hàng. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid1-1751333076.png)
2. Cho tam giác \[ABC\] nhọn \[\left( {AB < AC} \right)\] có hai đường cao \[BE,{\rm{ }}CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
b) Chứng minh: \(AF \cdot AB = AE \cdot AC\).
c) Đường thẳng qua \[B\] và song song với \[EF\] cắt \[AC\] tại \[M.\] Gọi \[I\] là trung điểm của \[BM,{\rm{ }}D\] là giao điểm của \[EI\] và \[BC.\] Chứng minh ba điểm \[A,{\rm{ }}H,{\rm{ }}D\] thẳng hàng.
Trong hộp kín có 6 viên bi đỏ, 3 viên bi xanh, các viên bi có cùng kích thước, khối lượng và hình dạng như nhau, chỉ khác màu sắc. Lấy ngẫu nhiên 1 viên bi từ trong hộp. Sau đó, thêm mỗi hộp một số viên bi màu đỏ, màu xanh sao cho xác suất chọn được viên bi mỗi màu không đổi. Hỏi cần thêm ít nhất bao nhiêu viên bi mỗi màu?