Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 4
29 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Hệ số góc của đường thẳng \(y = 4x - 3\) là
\(a = - 4.\)
\(a = - 3.\)
\(a = 3.\)
\(a = 4.\)
Biết rằng đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song, khi đó hệ số \(a\) bằng
\(1.\)
\(2.\)
\(3.\)
\(0.\)
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\({y^2} + 8x - 2022 = 0.\)
\(3x + 6 = 0.\)
\(3x - 2y - 9 = 0.\)
\(2{x^2} - 4 = 0.\)
Phương trình \(7 - 3x = 9 - x\) có tập nghiệm là
\(S = \left\{ 5 \right\}.\)
\(S = \left\{ 1 \right\}.\)
\(S = \left\{ { - 5} \right\}.\)
\(S = \left\{ { - 1} \right\}.\)
Cho tam giác \(ABC\) có \(DE\parallel BC\). Khẳng định nào sau đây là sai?
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC.\)
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC.\)
\(\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}}\) suy ra \(DE\parallel BC.\)
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC.\)
Cho \(\Delta ABC\) có \(AB = 4{\rm{ cm;}}\) \(AC = 9{\rm{ cm}}{\rm{.}}\) Gọi \(AD\) là tia phân giác của \(\widehat {BAC}\). Tỉ số \(\frac{{CD}}{{BD}}\) bằng
\(\frac{4}{9}.\)
\(\frac{9}{4}.\)
\(\frac{4}{5}.\)
\(\frac{5}{4}.\)
Cho tam giác \(ABC\) có \(I,K\) lần lượt là trung điểm của \(AB,AC\). Biết \(BC = 8{\rm{ cm}}\). Độ dài \(IK\) là
\(4{\rm{ cm}}{\rm{.}}\)
\({\rm{16 cm}}{\rm{.}}\)
\({\rm{2 cm}}{\rm{.}}\)
\({\rm{12 cm}}{\rm{.}}\)
Cho biết \(\widehat A = 50^\circ ;\widehat B = 60^\circ \). Khi đó số đo góc \(D\) bằng
\(50^\circ .\)
\(60^\circ .\)
\(70^\circ .\)
\(80^\circ .\)
Cho theo tỉ số \(k\). Vậy \(k\) bằng tỉ số nào dưới đây?
\(k = \frac{{AB}}{{BC}}\).
\(k = \frac{{AC}}{{DF}}\).
\(k = \frac{{DE}}{{AB}}.\)
\(k = \frac{{DE}}{{DF}}\).
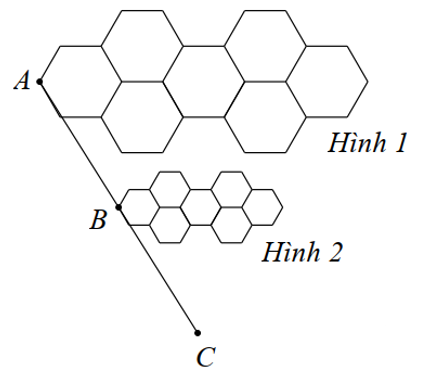
Cho hình bên. Biết Hình 1 đồng dạng phối cảnh với Hình 2 với tỉ số đồng dạng là \(2\). Khi đó tỉ số nào sau đây là đúng?
\(\frac{{AB}}{{BC}} = 2.\)
\(\frac{{AB}}{{AC}} = 2.\)
\(\frac{{AC}}{{AB}} = 2.\)
\(\frac{{BC}}{{AB}} = 2.\)
Một túi đựng các viên bi có hình dạng như nhau, chỉ khác màu. Trong đó có \(5\) viên bi màu đỏ, \(6\) viên bi màu xanh và \(3\) viên bi màu vàng. Lấy ngẫu nhiên một viên bi trong túi. Số kết quả có thể xảy ra là
\(6.\)
\(14.\)
\(3.\)
\(5.\)
Chọn ngẫu nhiên một số tự nhiên có một chữ số. Số kết quả có thể xảy ra là
\(7.\)
\(9.\)
\(10.\)
\(8.\)
a) \(AB\) là trung trực của \(NH.\)
b) \(EF\parallel MN.\)
c) \(\Delta AMN\) cân.
d) \(AI \bot EF.\)
a) Có \(6\) kết quả có thể xảy ra.
b) Có \(3\) kết quả thuận lợi cho biến cố “Mặt xuất hiện trên xúc xắc có số chấm là số chia hết cho \(2\)”.
c) Xác suất của biến cố “Mặt xuất hiện trên con xúc xắc có số chấm là số chia hết cho \(3\)” là \(0,5.\)
d) Xác suất của biến cố “Mặt xuất hiện trên con xúc xắc có số chấm là số chia hết cho \(5\) dư 1” là \(\frac{1}{3}.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\).
Tìm giá trị của \(x\) biết: \(2\left( {x + 17} \right) - \frac{{10}}{3}x = 10\).
Người ta dùng máy ảnh để chụp một người có chiều cao \(1,5{\rm{ m}}\) (như hình vẽ sau). Sau khi rửa phim thấy ảnh \(CD\) cao \({\rm{4 cm}}{\rm{.}}\)
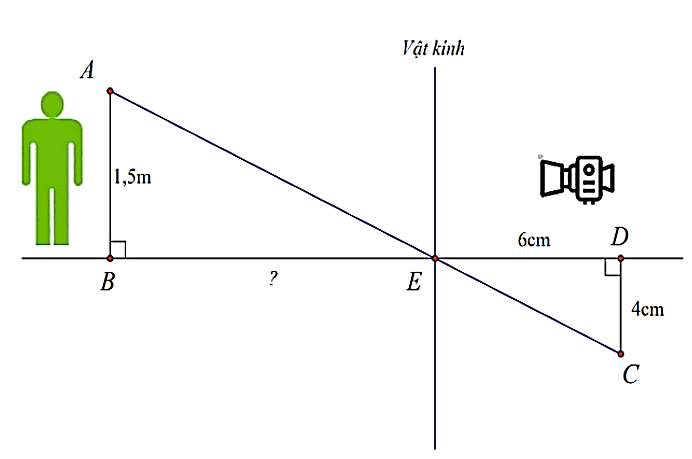
Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là \(ED = 6{\rm{ cm}}\). Hỏi khoảng cách từ người đó đến vật kính máy ảnh một đoạn \(BE\) là bao nhiêu centimet?
Bạn Cường vào cửa hàng Lotteria và dự định mua một suất gà rán. Khi đọc menu, bạn Cường thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá \(97{\rm{ }}000\) đồng, combo gà viên (ưu đãi) có giá \({\rm{84 }}000\) đồng, gà rán – 1 miếng có giá \({\rm{35 }}000\)đồng, gà rán – 2 miếng có giá \({\rm{68 }}000\) đồng, gà rán – 3 miếng có giá \({\rm{101 }}000\) đồng, cánh gà chiên – 3 miếng có giá \({\rm{48 }}000\) nghìn đồng. Bạn Cường cảm thấy món nào cũng ngon và dự định sẽ nhắm mắt chỉ tay chọn ngẫu nhiên một món. Tính xác suất “Món gà được bạn Cường chọn có giá dưới \({\rm{70 }}000\) đồng”.
(Kết quả ghi dưới dạng số thập phân)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cô Hương đầu tư \(400\) triệu đồng vào hai khoản: mua trái phiếu doanh nghiệp với lãi suất \(8\% \) một năm và mua trái phiếu chính phủ với lãi suất \(6\% \) một năm. Cuối năm cô Hương nhận được \(29\) triệu đồng tiền lãi. Hỏi cô Hương đã đầu tư vào mỗi khoản bao nhiêu tiền?
a) và
b) \(A{E^2} = EF.EG\).
c) \(BF.DG\) không đổi khi \(F\) thay đổi trên \(BC.\)
(0,5 điểm) Giải phương trình: \(\frac{{2027 - x}}{{73}} + \frac{{2025 - x}}{{75}} + \frac{{2023 - x}}{{77}} + \frac{{2021 - x}}{{79}} + 4 = 0\).