Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
29 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
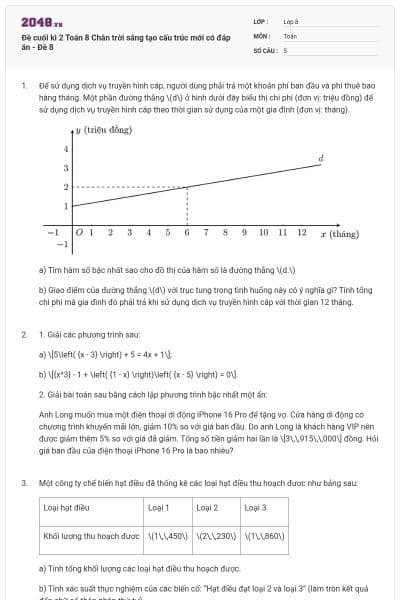
Mỗi câu lạc bộ tại trường Trung học cơ sở Kim Đồng có 15 học sinh. Số lượng học sinh nam và học sinh nữ của mỗi câu lạc bộ được biểu diễn trong bảng số liệu sau đây.
Biết trong biểu đồ trên có dữ liệu thống kê của câu lạc bộ chưa chính xác, đó là
Cầu lông.
Bóng bán.
Cờ vua.
Cầu lông, cờ vua.
Dữ liệu thu được về size áo bao gồm S, M, L của các nhân viên trong công ty là
Số liệu rời rạc.
Dữ liệu không là số, có thể sắp thứ tự.
Số liệu liên tục.
Dữ liệu không là số, không thể sắp thứ tự.
Tung một đồng xu, xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt \(N\)” bằng
\(\frac{1}{2}.\)
\(1.\)
\(2.\)
\(\frac{2}{1}.\)
Đội văn nghệ khối 8 của một trường có 3 học sinh nam lớp 8A, 3 học sinh nữ lớp 8B, 1 học sinh nam lớp 8C và 2 học sinh nữ lớp 8C. Chọn ngẫu nhiên một học sinh trong đội văn nghệ khối 8 để tham gia chương trình văn nghệ của trường. Số kết quả có thể xảy ra là:
\(6.\)
\(7.\)
\(8.\)
\(9.\)
Phương trình bậc nhất một ẩn \(ax + b = 0{\rm{ }}\left( {a \ne 0} \right)\) có nghiệm là
\(x = \frac{{ - b}}{a}.\)
\(x = \frac{b}{a}.\)
\(x = \frac{a}{b}.\)
\(x = \frac{{ - a}}{b}.\)
Cho các hình vẽ sau:
Đoạn thẳng \(MN\) là đường trung bình của tam giác \(ABC\) trong hình vẽ nào?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Năm nay tuổi con là \(x\) (tuổi) và tuổi mẹ gấp \(5\) lần tuổi con. Biểu thức biểu thị tuổi mẹ năm nay là
\(5x.\)
\(x - 5.\)
\(x:5.\)
\(x + 10.\)
Cho hình vẽ dưới đây:
Hệ thức theo Định lí Thalès của hình trên là
\(\frac{{CE}}{{CB}} = \frac{{CD}}{{CA}}\).
\(\frac{{BE}}{{CB}} = \frac{{CA}}{{AD}}\).
\(\frac{{CE}}{{BE}} = \frac{{AD}}{{CD}}\).
\(\frac{{DE}}{{AB}} = \frac{{AC}}{{AD}}\).
Cho tam giác \(ABC\), \(AD\) là đường phân giác của \(\widehat {BAC}\) \(\left( {D \in BC} \right)\). Tỉ lệ thức nào sau đây đúng?
\(\frac{{AB}}{{BD}} = \frac{{AC}}{{BC}}.\)
\(\frac{{AD}}{{AC}} = \frac{{BD}}{{DC}}.\)
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
\(\frac{{DB}}{{DC}} = \frac{{BC}}{{AC}}\).
Chọn khẳng định đúng.
Hai tam giác đồng dạng thì bằng nhau.
Hai tam giác bằng nhau thì đồng dạng.
Hai tam giác cân luôn đồng dạng.
Hai tam giác vuông luôn đồng dạng.
Cho , hãy chọn đáp án đúng.
\(\widehat M = \widehat R.\)
\(\frac{{MN}}{{QR}} = \frac{{NP}}{{QS}}.\)
\(\frac{{MN}}{{QR}} = \frac{{NP}}{{RS}}.\)
\(\widehat N = \widehat Q.\)
Nếu theo tỉ số \(k = \frac{2}{3}\) thì theo tỉ số
\(\frac{2}{3}.\)
\(\frac{3}{2}.\)
\(\frac{4}{9}.\)
\(\frac{4}{3}.\)
a) Cửa hàng đã thu thập dữ liệu trên bằng phương pháp thu thập trực tiếp.
b) Từ dữ liệu biểu đồ ta có bảng thống kê sau
Món ăn | Tỉ lệ phần trăm |
Phở | 45% |
Bún bò | 18% |
Bánh mì | 25% |
Gỏi cuốn | 12% |
c) Có hơn \(450\) khách hàng lựa chọn món Phở.
d) Dựa vào biểu đồ, nếu cửa hàng muốn kinh doanh một món ẩm thực duy nhất thì nên ưu tiên chọn món Phở.
a) \(\frac{{BD}}{{AD}} = \frac{{MB}}{{MA}}.\)
b) \(DE\parallel BC\).
c) \(DI = EI.\)
d) \(ED = 6{\rm{ cm}}{\rm{.}}\)
Biểu đồ cột biểu diễn sản lượng khoai lang ơ rPhus Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn)
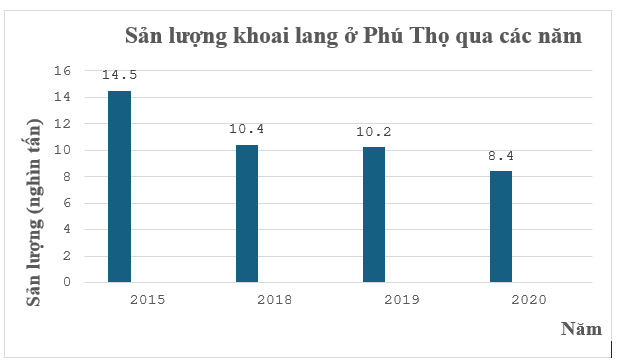
Năm 2019 sản lượng khoai lang ở Phú Thọ giảm bao nhiêu phần trăm so với năm 2015?
(Kết quả làm tròn đến hàng phần mười)
Một hộp có \(50\) chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số sau \(1;2;3;4,....;49;50,\) hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số trên thẻ được rút ra là vừa là bình phương của một số và vừa chia hết cho \(3\)”.
(Kết quả ghi dưới dạng số thập phân)
Tính giá trị của \(x\), biết: \({x^3} - 1 + \left( {1 - x} \right)\left( {x - 5} \right) = 0\).
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao \(1,5{\rm{ m}}\) so với mặt đất, chân cọc cách gốc cây \({\rm{8 m}}\) và cách bóng của đỉnh cọc \({\rm{2 m}}\).

Hỏi chiều cao của cây là bao nhiêu mét? (Kết quả làm tròn đến chữ số thập phân thứ nhất)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một tàu hỏa từ Hà Nội đi TP. Hồ Chí Minh. Sau 1 giờ 48 phút, một tàu hỏa khác khởi hành từ Nam Định cũng đi TP. Hồ Chí Minh với vận tốc nhỏ hơn vận tốc của tàu thứ nhất \(5{\rm{ km/h}}{\rm{.}}\) Hai tàu gặp nhau tại một nhà ga sau 4 giờ 48 phút kể từ khi tàu thứ nhất khởi hành. Tính vận tốc của mỗi tàu, biết rằng ga Nam Định nằm trên đường từ Hà Nội đi TP. Hồ Chí Minh và cách ga Hà Nội \(87{\rm{ km}}{\rm{.}}\)
a) Chứng minh rằng .
b) Chứng minh rằng \(B{C^2} = BD.DH.\)
c) Kẻ \(DE\) là đường phân giác của tam giác \(ABD\). Gọi \(I\) là giao điểm của \(DE\) và \(AH\). Chứng minh \(\Delta AIE\) cân và \(A{E^2} = IH.EB.\)
(0,5 điểm) Giải phương trình: \({\left( {2024 - x} \right)^3} + {\left( {2026 - x} \right)^3} + {\left( {2x - 4050} \right)^3} = 0\).