Bộ 5 đề thi giữa kì 1 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
21 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Biểu diễn tập hợp \[H = \left\{ {2;\,\,4;\,\,6;\,\,8;\,\,10} \right\}\] bằng cách chỉ ra tính chất đặc trưng của nó là
\[H = \left\{ {x \in \mathbb{N}|x} \right.\] là số chẵn và \(\left. {x \le 10} \right\}.\)
\[H = \left\{ {x \in \mathbb{N}|x} \right.\] là số chẵn và \(\left. {x < 10} \right\}.\)
\[H = \left\{ {x \in \mathbb{N}*|x} \right.\] là số chẵn và \(\left. {x \le 10} \right\}.\)
\[H = \left\{ {x \in \mathbb{N}*|x < 10} \right\}.\]
Khi thêm I vào phía trước số La Mã XX, phát biểu đúng là
Số ban đầu có giá trị giảm xuống \(1\) đơn vị.
Số ban đầu có giá trị tăng thêm \(1\) đơn vị.
Số mới có giá trị trong hệ thập phân là \(21.\)
Không thể thêm vào như thế vì trái với quy tắc viết số La Mã.
Biểu thức nào sau đây sử dụng đúng dấu ngoặc?
\[200:\left( {2 \cdot \left[ {20 - \left\{ {\left. {10 + 5} \right\}} \right.} \right]} \right).\]
\(200:\left\{ {\left. {2 \cdot \left( {20 - \left[ {10 + 5} \right]} \right)} \right\}} \right..\)
\(200:\left\{ {\left. {2 \cdot \left[ {20 - \left( {10 + 5} \right)} \right]} \right\}} \right..\)
\(200:\left[ {2 \cdot \left\{ {\left. {20 - \left( {10 + 5} \right)} \right\}} \right.} \right].\)
Kết quả của phép tính \({a^m}:{a^n}\) là
\({a^{m\,\,:\,\,n}}.\)
\({a^{m\,\, \cdot \,\,n}}.\)
\({a^{m - n}}.\)
\({\left( {{a^m}} \right)^n}.\)
Kết quả của phép tính \({2^{15}}:\left( {{2^6} \cdot 32} \right)\) viết dưới dạng lũy thừa của cơ số 4 có số mũ là
1.
2.
3.
4.
Những số nào sau đây là ước của 36?
2; 3; và 6.
0; 1 và 6.
12; 18 và 24.
36; 72 và 108.
Khẳng định nào sau đây là sai?
Một số chia hết cho 3 thì số đó chia hết cho 9.
Một số chia hết cho 9 thì số đó chia hết cho 3.
Một số chia hết cho 10 thì số đó chia hết cho 5.
Một số chia hết cho 45 thì số đó chia hết cho 9.
Bạn An có ngày sinh là số nguyên tố lớn nhất nhỏ hơn 20, tháng sinh của bạn là số nguyên tố nhỏ nhất. Vậy bạn An có ngày và tháng sinh là bao nhiêu?
Ngày \[19\] tháng \[3.\]
Ngày \[19\] tháng \[2.\]
Ngày \[7\] tháng \[2.\]
Ngày \[7\] tháng \[3.\]
Cho hình vẽ sau:
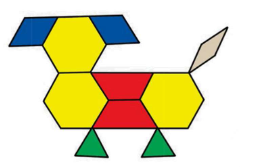
Trong hình vẽ trên có:
2 hình thang, 3 hình lục giác đều, 3 hình tam giác đều.
2 hình thoi, 3 hình lục giác đều, 2 hình thang cân.
3 hình lục giác đều, 2 hình thang cân, 2 hình tam giác đều.
2 hình tam giác đều, 1 hình lục giác đều, 4 hình thoi.
Hình nào trong các hình sau có 2 cạnh đối song song và 2 đường chéo bằng nhau?
Hình bình hành.
Hình thang cân.
Hình thoi.
Hình tam giác đều.
Khẳng định nào sau đây là sai?
Hình chữ nhật và hình thoi có các cặp cạnh đối song song với nhau.
Hình lục giác đều có ba đường chéo chính bằng nhau.
Hình bình hành có hai cạnh đối bằng nhau.
Hình thoi có hai đường chéo bằng nhau.
Một hình bình hành có độ dài cạnh đáy là \(a\) và diện tích là \(S\) thì có chiều cao tương ứng với cạnh đáy đã cho là
\(h = \frac{S}{a}.\)
\(h = \frac{S}{{2a}}.\)
\(h = \frac{{2S}}{a}.\)
Cả A, B, C đều sai.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho số tự nhiên có hai chữ số.
a) Trong các số đã cho, có 10 số chia hết cho cả 2 và 5.
b) Trong các số đã cho, có 29 số chia hết cho 3.
c) Trong các số đã cho, có 5 số là chia hết cho cả 2 và 9.
d) Tổng của các số là bội của 18 khi phân tích thành nhân tử được thừa số có số mũ cao nhất là 3.
Cho hình vuông \(ABCD\) có cạnh bằng 4 cm. Khi đó
a) \(AB = BC = CD = DA = 4{\rm{\;cm}}.\)
b) \(AC\) và \(BD\) song song với nhau.
c) Mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(60^\circ .\)
d) Vẽ cạnh \(AB = 4{\rm{\;cm}}{\rm{.}}\) Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}.\) Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Có bao nhiêu số tự nhiên \(m\) sao cho \(2125 < m < 2154\) và chia hết cho 9?
Có bao nhiêu số tự nhiên \(n\) thỏa mãn \(25 < {3^n} < 260?\)
Một trường Trung học cơ sở có 997 học sinh tham dự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều có chỗ ngồi?
Một hình thoi có diện tích là 220 cm2 và độ dài đường chéo lớn là 22 cm. Tính độ dài đường chéo nhỏ của hình thoi đó (đơn vị: cm).
B. TỰ LUẬN (3,0 điểm)
(1,5 điểm)
1) Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(39 - 125:\left[ {\left( {{5^{11}} \cdot 16 + 9 \cdot {5^{11}}} \right):{5^{12}}} \right].\) b) \(57 \cdot 34 + 100 \cdot 43 + 57 \cdot 66.\)
2) Tìm \(x,\) biết: \(121 + \left( {5x - 21} \right):4 = 127.\)
(1,0 điểm) Một khu đất hình thang cân \[ABCD\] có độ dài các cạnh đáy lần lượt là 30 m và 36 m và chiều cao là 25 m. Trong khu đất đó, người ta đào một cái ao hình vuông \[EFGH\] như hình vẽ, phần đất còn lại trồng hoa.

a) Tính diện tích phần đất trồng hoa, biết \[EF\] = 15 m.
b) Để giữ bờ, người ta trồng cây xung quanh bờ ao, biết rằng cây đầu tiên trồng ở điểm \[E\] và cứ 3 m thì người ta trồng một cây. Hỏi quanh bờ ao, trồng được bao nhiêu cây?
(0,5 điểm) Cho biểu thức \(A = 2 + {21^{23}} + {25^{125}}.\) Chứng minh rằng \(A\) là hợp số.








