Bộ 10 đề thi giữa kì 1 Toán 6 Kết nối tri thức có đáp án - Đề 7
14 câu hỏi
Cho tập hợp \(A = \left\{ {0;\,\,1;\,\,2;\,\,a;\,\,b} \right\}\). Cách viết sai là
\(0 \in A\)
\(b \notin A\)
\(5 \notin A\)
\(c \notin A\).
Viết số \(29\) bằng số La Mã là
\(XXVIIII\)
\(XIX\)
\(XXIV\)
\(XXIX\).
Biểu thức \(A = {2^{2023}} - {2^{2022}} + 1\) bằng biểu thức nào dưới đây?
\({2^{2023}} - 1\)
\({2^{2022}} + 2\)
\({2^{2022}} + 1\)
\({2^{2023}} + 1\).
Chữ số điền vào dấu \(*\) để số \(\overline {34*} \) chia hết cho \(2\) là:
0; 2; 4; 6; 8
\(1;\,\,3;\,\,5;\,\,7\)
\(0\)
\(0;\,\,2;\,\,4;\,\,6;\,\,8;\,\,...\).
Trong các số sau, số nào là số nguyên tố
12
13
15
18.
Khẳng định nào sau đây là sai?
Trong tam giác đều ba góc bằng nhau
Hình lục giác đều có ba đường chéo chính bằng nhau
Hình thoi có hai đường chéo vuông góc với nhau
Hình thang cân có hai góc kề cạnh bên bằng nhau.
Chọn câu sai. Cho \[ABCD\] là hình bình hành. Khi đó:
\[AB\; = \;CD\]
\[AD\; = BC\]
\[AB\parallel CD\]
\[AC = \;BD\].
Xếp 9 mảnh hình vuông nhỏ bằng nhau tạo thành hình vuông \[MNPQ\]. Biết \[MN = 9\] cm. Diện tích của hình vuông nhỏ là
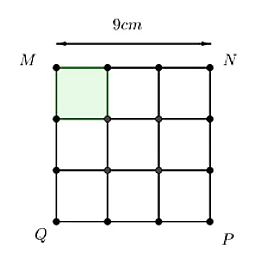
9 cm2
1 cm2
12 cm2
81 cm2.
(a) Viết tập hợp \[A\] các chữ cái trong từ “GIÁO VIÊN”.
(b) Cho biết tập hợp \(A\) là tập hợp các số tự nhiên lớn hơn \(17\) và không vượt quá \(23\) bằng cách hai cách.
Một đội thiếu niên khi xếp hàng 2; 3; 4; 5 đều thừa một người. Biết số đội viên trong khoảng 100 đến 150 người. Tính số đội viên thiếu niên của đội.
Thực hiện phép tính (tính nhanh nếu có thể):
(a) \[667--195\,\,.\,\,93:465 + 372\]
(b) \[317\,\,.\,\,124 - 317\,\,.\,\,23 - 317\]
(c) \[3\,\,.\,\,{2^6}\,\,.\,\,125\]
(d) \[12 + 3\,\,.\,\,\left\{ {90:\left[ {39 - {{\left( {{2^3} - 5} \right)}^2}} \right]} \right\}\].
Tìm \[x\], biết:
(a) \[200-8\,\left( {2x + 7} \right) = 112\]
(b) \[3x - {2^4} = {5^3}\].
(a) Vẽ hình vuông \[MNPQ\] biết độ dài một cạnh bằng 5 cm.
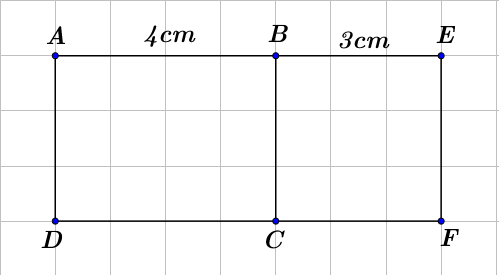
(b) Cho hình vẽ, biết \[ABCD\] là hình chữ nhật và \[BEFC\] là hình vuông. Biết \[AB\; = 4\] cm và \[BE = 3\] cm. Tính diện tích hình chữ nhật \[AEFD\].
Cho \(A = 7 + {7^2} + {7^3} + ... + {7^{119}} + {7^{120}}\). Chứng minh rằng biểu thức \[A\] chia cho hết cho 57.








