12 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Một chiếc đồng hồ có kim giờ \(OM\) chỉ số 12, kim phút \(ON\) chỉ số 3.
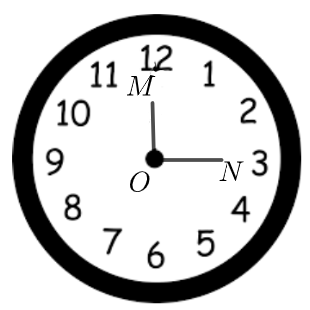
Số đo của góc lượng giác \(\left( {OM,ON} \right)\) là
\[ - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
\[ - \frac{{3\pi }}{2} + k2\pi ,k \in \mathbb{Z}\].
\[\pi + k2\pi ,k \in \mathbb{Z}\].
\[\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
Cho \(\cos \alpha = \frac{1}{3}\). Khi đó \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{1}{3}.\)
\(\frac{2}{3}.\)
\( - \frac{2}{3}.\)
\(\frac{1}{3}.\)
Cho hàm số \(y = \cos x\) có đồ thị như hình vẽ dưới đây:
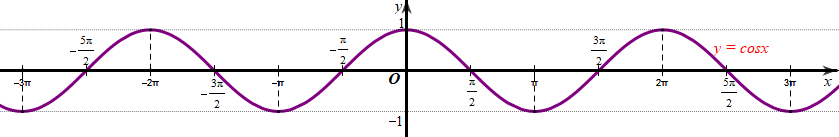
Hàm số \(y = \cos x\) đồng biến trên khoảng nào dưới đây?
\(\left( {0;\pi } \right)\).
\(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
\(\left( { - 3\pi ; - 2\pi } \right)\).
Tìm nghiệm của phương trình \(\sin 2x = 1\).
\(x = \frac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{2} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{k\pi }}{2}{\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{2{n^2} - 1}}{{{n^2} + 3}}\). Tìm số hạng \({u_5}\).
\({u_5} = \frac{{17}}{{12}}.\)
\({u_5} = \frac{{71}}{{39}}.\)
\({u_5} = \frac{7}{4}.\)
\({u_5} = \frac{1}{4}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_n} = 5 - 2n\). Tìm công sai của cấp số cộng.
\(d = - 2\).
\(d = 1\).
\(d = 3\).
\(d = 2\).
Trong các dãy số \(\left( {{u_n}} \right)\)sau đây, dãy số nào là cấp số nhân?
\({u_n} = \frac{1}{n}\).
\({u_n} = 3n\).
\({u_n} = {2^n} + 1\).
\({u_n} = {2^n}\).
Mệnh đề nào sau đây là đúng?
\(\lim {\left( {\frac{1}{2}} \right)^n} = \frac{1}{2}\).
\(\lim \frac{1}{{{n^2}}} = + \infty \).
\(\lim {n^3} = 0\).
\(\lim \left( { - {n^2}} \right) = - \infty \).
Tính giới hạn \(L = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 3}}{{ - 4x + 2}}\).
\(L = 1\).
\(L = \frac{1}{2}\).
\(L = - \frac{1}{2}\).
\(L = - \frac{3}{4}\).
Cho \(\cos x = \frac{1}{3}\left( { - \frac{\pi }{2} < x < 0} \right)\). Giá trị của \(\tan 2x\) là
\(\frac{{4\sqrt 2 }}{7}\).
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{4\sqrt 2 }}{7}\).
\( - \frac{{\sqrt 5 }}{2}\).
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
\(y = {\tan ^2}x\).
\(y = \cos 3x \cdot \sin x\).
\(y = \cos x + \sin x\).
\(y = \cos x \cdot {\sin ^2}x\).
Cho dãy số \(\left( {{u_n}} \right),\) biết \({u_n} = \frac{{2n + 5}}{{5n - 4}}.\)Số \(\frac{7}{{12}}\) là số hạng thứ bao nhiêu của dãy số?
8.
6.
9.
10.
