Bộ 5 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Kết quả của phép cộng hai đơn thức \(2x{y^2}z\) và \( - {x^2}yz\) là
Một đơn thức.
Một đa thức nhưng không phải đơn thức.
Một số.
Không xác định.
Bậc của đa thức \(A = {x^6} + {y^5} + {x^4}{y^4} + 1\) là
4.
5.
6.
8.
Đẳng thức nào sau đây là hằng đẳng thức?
\[4{a^2} - 1 = 3a\].
\[\left( {a + 2} \right)\left( {a - 2} \right) = {a^2} - 4\].
\[5a\; = 3a + 1\].
\[{a^2} - 1 = 2a + 1\].
Khẳng định nào sau đây là đúng?
\(\frac{A}{B} = \frac{{ - A}}{{ - B}}.\)
\(\frac{A}{B} = \frac{A}{{ - B}}.\)
\(\frac{A}{B} = \frac{{ - A}}{B}.\)
\(\frac{A}{B} = - \frac{{ - A}}{{ - B}}.\)
Nhận định nào sau đây là đúng?
Nếu hình chóp có đáy là hình thoi, chân đường cao trùng với tâm hình thoi thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình chữ nhật, chân đường cao trùng với giao điểm của hai đường chéo đáy thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình vuông thì nó là hình chóp đều.
Nếu hình chóp có đáy là tam giác đều, chân đường cao trùng với trọng tâm của tam giác thì nó là hình chóp đều.
Cho hình chóp tam giác đều \(A.BCD\) như hình vẽ bên. Đoạn thẳng nào sau đây là trung đoạn của hình chóp?
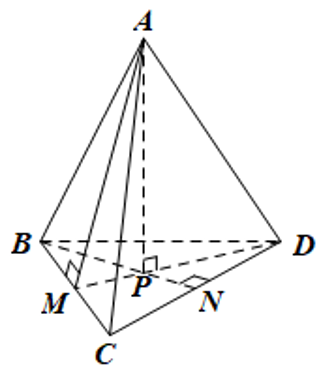
\(AC\).
\(AM\).
\(BN\).
\(AP\).
Cho tam giác \(ABC\) có đường cao \(AH.\) Biết \(AC = 15\;\;{\rm{cm}},\,\,AH = 12\;\;{\rm{cm,}}\,\,BH = 9\;\;{\rm{cm}}.\) Hỏi tam giác \(ABC\) là tam giác gì?
Tam giác cân.
Tam giác vuông.
Tam giác cân.
Tam giác tù.
Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là
hình thang cân.
hình chữ nhật.
hình bình hành.
hình thoi.
Trong các hình thức thu thập dữ liệu sau đây, đâu là hình thức thu thập dữ liệu trực tiếp?
Tìm tài liệu có sẵn trên Internet.
Quan sát.
Tìm thông tin từ trong sách, báo.
Tin tức từ TV.
Trước trận tứ kết World Cup 2022, một website điện tử đã khảo sát độc giả với câu hỏi “Theo bạn, đội bóng nào sẽ vô địch World Cup 2022?”. Dữ liệu mà website thu được là
Số liệu rời rạc.
Dữ liệu không là số, có thể sắp thứ tự.
Số liệu liên tục.
Dữ liệu không là số, không thể sắp thứ tự.
Cho biểu đồ sau:
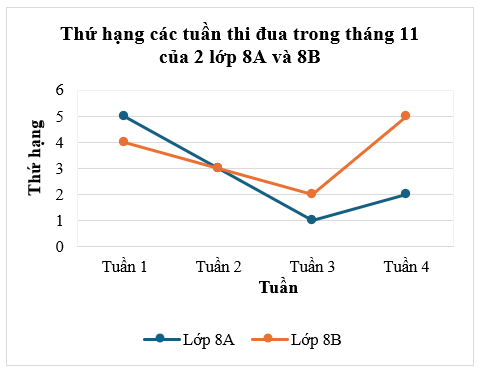
Hỏi tuần nào mà hai lớp 8A và 8B có cùng thứ hạng thi đua?
Tuần 1.
Tuần 2.
Tuần 3.
Tuần 4.
Thành phần của một loại thép được biểu diễn trong biểu đồ dưới đây:
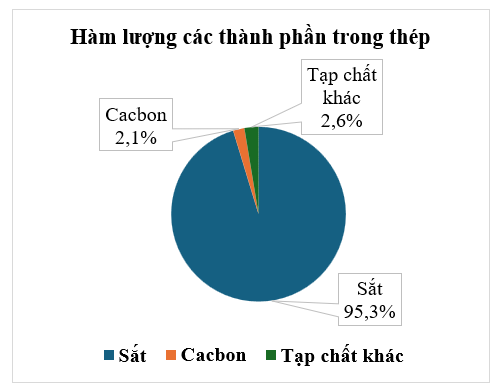
Khối lượng sắt trong một thanh thép nặng 1 kg là
953 g.
26 g.
21 g.
\[95,3{\rm{ g}}{\rm{.}}\]
Cho đa thức \(U = \left( {10{x^5}{y^3} - 25{x^3}{y^2} + 20{x^4}{y^3}} \right):\left( { - 5{x^2}{y^2}} \right)\) và \(V = 2{x^2}y\left( {x + 2} \right)\).
a) Hệ số cao nhất của của đa thức \(U\) là 5.
b) Giá trị của biểu thức \(U\) tại \(x = - 1\,;\,\,y = 2\) là 10.
c) Bậc của đa thức \(V\) là 4.
d) Tổng của hai đa thức \(U\) và \(V\) chia hết cho 5.
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\) là một điểm bất kì trên cạnh huyền \(BC\). Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(M\) xuống \(AB\) và \(AC.\) Lấy điểm \(I\) sao cho \(A\) là trung điểm của \(ID\); điểm \(K\) sao cho \(M\) là trung điểm của \(EK\).
a) \(IA = ID\,;\,\,KM = KE.\)
b) Tứ giác \(ADME\) là hình chữ nhật.
c) Tứ giác \(ADMC\) là hình thang cân.
d) \(DK\,{\rm{//}}\,EI\).
Cho biểu thức \[T = \left( {{x^2} - 6x + 12} \right)\left( {x - 6} \right) - {\left( {x - 4} \right)^3}\]. Giá trị của biểu thức \[T\] bằng bao nhiêu?
Cho biểu thức \[I = \frac{{{{\left( {x + 2} \right)}^2}}}{x} \cdot \left( {1 - \frac{{{x^2}}}{{x + 2}}} \right) - \frac{{{x^2} + 6x + 4}}{x}\,\,\,\left( {x \ne 0\,;\,\,x \ne 2} \right)\]. Hỏi sau khi rút gọn biểu thức \[I\] ta được đa thức có bậc là bao nhiêu?
Một kho chứa có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 6 m và trung đoạn là \[3{\rm{ m}}.\] Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ phần cửa có diện tích là \[7{\rm{ }}{{\rm{m}}^{\rm{2}}}.\] Biết rằng cứ mỗi mét vuông sơn cần trả \[50\,\,000\] đồng. Tính số tiền cần trả để hoàn thành việc sơn phủ đó theo đơn vị triệu đồng?
![Một kho chứa có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 6 m và trung đoạn là \[3{\rm{ m}}.\] Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ p (ảnh 1)](https://video.vietjack.com/upload2/images/1752817036/1752817098-image6.png)
Tìm \(x\) trong hình vẽ dưới đây theo đơn vị độ.
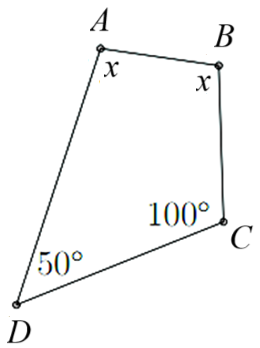
(1,5 điểm) Quan sát biểu đồ sau:
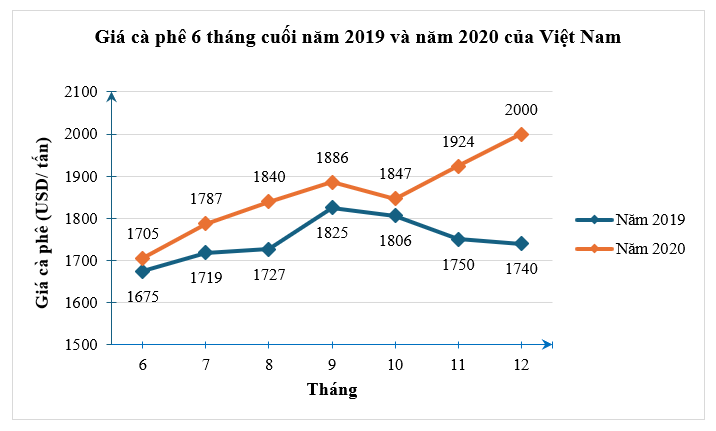
(Nguồn: Hiệp hội Cà phê – Ca cao Việt Nam)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Lập bảng thống kê tương ứng cho dữ liệu trong biểu đồ trên. Nếu chọn một biểu đồ khác để biểu diễn dữ liệu đó, ta nên chọn loại biểu đồ gì?
c) Tìm ra một tháng trong sáu tháng cuối năm 2020 có sự gia tăng giá cà phê mạnh nhất so với cùng kì năm trước.
(0,5 điểm) Cho \({a^2} + {b^2} + {c^2} = ab + bc + ca\) và \(a + b + c = 2025.\) Tính \(a,\,\,b,\,\,c.\)
(1,0 điểm) Cho tam giác \(ABC\) vuông ở \(A.\) Gọi \(G\) là trung điểm của \(BC.\) Qua \(G\) kẻ \(GE \bot AB\) \(\left( {E \in AB} \right)\) và \(GF \bot AC\) \(\left( {F \in AC} \right).\) Từ \(E\) kẻ đường thẳng song song với \(BF,\) đường thẳng này cắt \(GF\) tại \(I.\)
a) Chứng minh tứ giác \(BEIF\) là hình bình hành.
b) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(AGCI\) là hình vuông.








