Bộ 10 đề thi giữa kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 5
37 câu hỏi
Đơn thức \( - 36{a^2}{b^2}{x^2}{y^3}\) (với \(a,b\) là hằng số) có hệ số là
\[ - 36{a^2}{b^2}\].
\[ - 36\].
\[36{a^2}{b^2}\].
\[ - 36{a^2}\].
Bậc của biểu thức \(A = 2{x^2}y \cdot 5x{y^3}\) là
\(5\).
\(6\).
\(7\).
\(8\).
Cho các đơn thức \(A = 4{x^3}y\left( { - 5xy} \right)\), \(B = {x^4}{y^2}\), \(C = - 5{x^2}{y^4}\). Các đơn thức nào sau đây đồng dạng với nhau?
Đơn thức \(A\) và đơn thức \(C\).
Đơn thức \(B\) và đơn thức \(C\).
Đơn thức \(A\) và đơn thức \(B\).
Cả ba đơn thức \(A,B,C\) đồng dạng với nhau.
Điều kiện của số tự nhiên \(n\)để phép chia \(\left( {4{x^{10}}y - x{y^7} + {x^5}{y^4}} \right):2{x^n}{y^n}\)là phép chia hết là
\(n = 0\).
\(n = 1\).
\(n = 5\).
\(n \in \left\{ {0\,;\,\,1} \right\}\).
Đẳng thức nào sau đây là hằng đẳng thức?
\({x^2} - x = - x + {x^2}\).
\(x\left( {x - 1} \right) = x - {x^2}\).
\({\left( {a - b} \right)^2} = - {\left( {b - a} \right)^2}\).
\(a - 2 = 2 - a\).
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).
\(xy\left( {14x - 21y + 28xy} \right)\).
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\).
\(7xy\left( {2x - 3y + 4xy} \right)\).
Hình dưới đây là một bóng đèn có 4 mặt bên là các tam giác cân, 1 mặt đáy là hình vuông. Bóng đèn như vậy có dạng là hình gì? 
Hình chóp tứ giác đều.
Hình chóp tam giác đều.
Hình lăng trụ tứ giác.
Hình tam giác.
Thể tích của hình chóp là
tích nửa chu vi đáy và đường cao của hình chóp.
tích nửa chu vi đáy và trung đoạn.
một phần ba tích diện tích đáy và chiều cao.
một phần b tích diện tích đáy và trung đoạn.
Hình chóp tứ giác đều có cạnh đáy là \(1\) cm. Khi đó chu vi đáy của hình chóp này là
\(3\,\,{\rm{cm}}\).
\(4\,\,{\rm{cm}}\).
\(5\,\,{\rm{cm}}\).
\(6\,\,{\rm{cm}}\).
Hình chóp tam giác đều có một mặt bên là tam giác đều có diện tích bằng \(a\), khi đó diện tích tất cả các mặt của hình chóp tam giác đều đó là
\(3a\).
\(4a\).
\(5a\).
\(6a\).
Cho tam giác \[ABC\]có độ dài ba cạnh \[AB = 6{\rm{ cm}},{\rm{ }}BC = 8{\rm{ cm}},{\rm{ }}AC = 10{\rm{ cm}}.\]Khẳng định nào sau đây là đúng?
Tam giác \[ABC\] vuông tại\[A\].
Tam giác \[ABC\] vuông tại\[B\].
Tam giác \[ABC\] vuông tại\[C\].
Tam giác \[ABC\] đều.
Trong các khẳng định sau, khẳng định nào đúng?
Tứ giác có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 3 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 4 đường chéo, 4 đỉnh và 4 góc.
Tứ giác có 4 cạnh, 1 đường chéo, 4 đỉnh và 4 góc.
Cho hai biểu thức \(A\) và \(B\) thỏa mãn \(45{x^6}{y^3}:A = 5{x^3}{y^2}\) và \(\left( {B + 7{x^4}{y^2}} \right):A = 3x{y^2} + 2xy.\)
a) Biểu thức là đơn thức bậc 3.
b) Với \(x = - 1\,;\,\,y = 2\) thì giá trị của biểu thức \(A\) bằng \( - 18.\)
c) Đa thức \(B\) có hai hạng tử.
d) Tích của hai biểu thức \(A\) và \(B\) là \(36{x^7}{y^5} + 20{x^7}{y^3}.\)
Bạn Uyên dự định làm 4 hộp quà có dạng hình chóp tứ giác đều như hình bên có cạnh đáy \(6{\rm{ cm}}{\rm{,}}\) chiều cao của mặt bên xuất phát từ đỉnh là \(4{\rm{ cm}}{\rm{.}}\)
a) Mỗi hộp quà có 5 mặt.
b) Diện tích xung quanh của một hộp quà là\(48{\rm{ c}}{{\rm{m}}^2}\).
c) Diện tích các mặt của hộp quà là\(60{\rm{ c}}{{\rm{m}}^2}\).
d) Diện tích giấy mà bạn Uyên cần dùng để làm 4 hộp quà \(240{\rm{ c}}{{\rm{m}}^2}.\) 
Cho đa thức \(A = - \frac{1}{3}x{y^2} + \frac{1}{2}{x^2}y + x{y^2} - \frac{3}{4}{x^2}y.\) Tính giá trị của \(A\) tạ\(x\,,\,\,y\)i \(x = - 2;y = 3\).
Cho hai số thỏa mãn\(x - y = 5\) và \(xy = 3\). Tính giá trị\({x^2} + {y^2}\).
Từ một khúc gỗ hình lập phương cạnh \[30{\rm{ cm}}{\rm{.}}\] Người ta cắt đi một phần gỗ để được phần còn lại là một hình chóp tứ giác đều có đáy là hình vuông cạnh \[30{\rm{ cm}}\] và chiều cao của hình chóp cũng bằng \[30{\rm{ cm}}{\rm{.}}\] Tính thể tích của phần gỗ bị cắt đi (đơn vị: \[d{m^3}).\]
Tứ giác \(ABCD\) có \(\widehat C = 50^\circ ,\,\,\widehat D = 60^\circ ,\,\,\widehat A:\widehat B = 3:2.\) Tính \(2\widehat A - \widehat B\) (đơn vị: độ).
Phân tích mỗi đa thức sau thành nhân tử:
a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\). b) \[{x^4} + {x^3} + 2{x^2} + x + 1\]. c) \({x^3} + 2{x^2} + x - 16x{y^2}\).
1.Một viên bi lăn từ vị trí \(A\) đến vị trí \(D\) theo đường gấp khúc \(ABCD\) hết 21 giây, biết rằng \(AB = 10{\rm{\;cm}},\)\(BC = 12{\rm{\;cm}},\)\(CD = 6{\rm{\;cm}}\) (hình vẽ bên). Hỏi nếu viên bi đó lăn theo đoạn thẳng \(AD\) thì hết bao nhiêu giây? Giả sử vận tốc của viên bi không thay đổi. 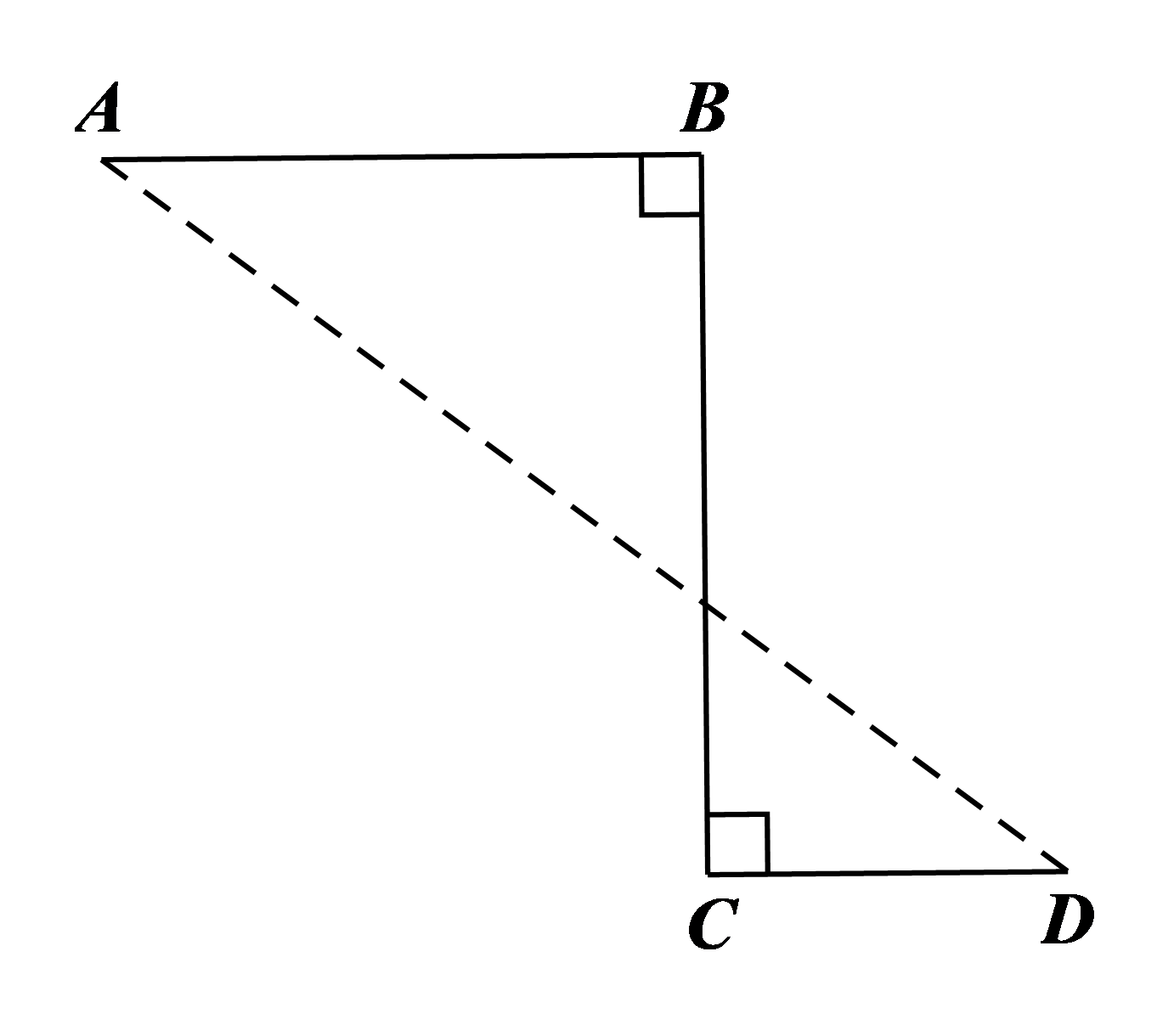
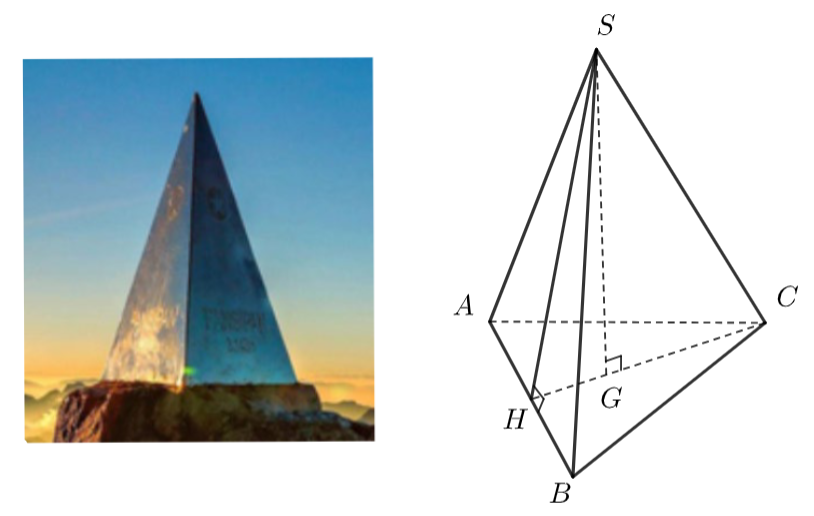
2. Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m}}{\rm{,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm}}{\rm{,}}\)chiều cao \(90{\rm{ cm}}\). Đỉnh Fansipan được minh họa bằngbởi hình chóp tam giác đều \(S.ABC\). Đường cao của mặt đáy là \(CH\,;\,\,G\)là trọng tâm của mặt đáy(như hình vẽ).
Trong các biểu thức đại số sau, biểu thức nào không phải là đơn thức?
\( - x\).
\( - \frac{5}{6}\).
\(\frac{x}{2}\).
\(\frac{2}{x}\).
thực hiện phép tính nhân \(x\left( {2{x^2} + 1} \right)\) ta được kết quả
\(3{x^2} + x\).
\(3{x^3} + x\).
\(2{x^3} + x\).
\(2{x^3} + 1\).
Thực hiện phép chia \(\left( {2{x^4}y - 6{x^2}{y^7}} \right):\left( {2{x^2}} \right)\) ta được đa thức \[a{x^2}y + b{y^7}\](\(a,\,\,b\) là hằng số). Khi đó \(a + b\) bằng
\( - 3\).
\( - 4\).
\( - 2\).
\( - 5\).
Điền vào chỗ trống sau: .
\[2\].
\[4\].
\[8\].
\[16\].
Hệ số tự do của đa thức \(M = {\left( {x + 2} \right)^3} - {\left( {x - 2} \right)^3} + \left( {x - 4} \right)\left( {x + 4} \right)\) sau khi thu gọn là
\[21\].
\[16\].
\[0\].
\[ - 16\].
Chọn đáp án đúng. Với đa thức \[B\] khác đa thức \[0\] thì ta có
\[\frac{A}{B} = \frac{{A\,.\,M}}{{B\,.\,M}},\,\,M\] là một đa thức khác đa thức \[0\].
\[\frac{A}{B} = \frac{{A + M}}{{B + M}}\].
\[\frac{A}{B} = \frac{{A - M}}{{B - M}}\].
\[\frac{A}{B} = \frac{{A\,.\,M}}{{B\,.\,M}}\].
Kết quả của phép tính \(\frac{1}{{2x - 1}} + \frac{1}{{2x + 1}}\) là
\[\frac{{4x}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}}\].
\[\frac{{4x - 2}}{{\left( {2x - 1} \right)\left( {2x + 1} \right)}}\].
\[\frac{{3x}}{{5\left( {{x^2} + 4} \right)}}\].
\[\frac{x}{{5\left( {{x^2} + 4} \right)}}\].
Hình chóp tam giác đều có chiều cao là \[h\], diện tích đáy là \[S\]. Khi đó, thể tích \[V\] của hình chóp đều bằng
\(V = 3S\,.\,h\).
\(V = S\,.\,h\).
\(V = \frac{1}{2}S\,.\,h\).
\(V = \frac{1}{3}S\,.\,h\).
Cho hình chóp tứ giác đều \(S.ABCD\) (như hình vẽ). Khi đó, trung đoạn của hình chóp là
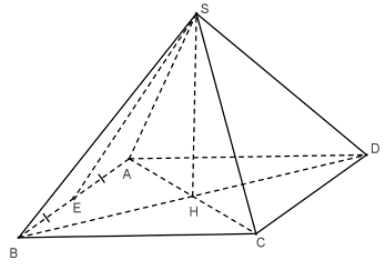
\[SA\].
\[SE\].
\[SC\].
\[SH\].
Tính thể tích hình chóp tam giác đều có cạnh đáy bằng \({\rm{5}}\;{\rm{cm}}\), chiều cao \({\rm{4}}\;{\rm{cm}}\).
\[{\rm{25}}\sqrt {\rm{3}} \;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[\frac{{{\rm{25}}\sqrt {\rm{3}} }}{{\rm{3}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[\frac{{{\rm{125}}\sqrt {\rm{3}} }}{{\rm{4}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[\frac{{{\rm{25}}\sqrt {\rm{3}} }}{{{\rm{14}}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
Cho hình chóp tứ giác đều có thể tích bằng \({\rm{50}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}\) chiều cao là \({\rm{6}}\;{\rm{cm}}\). Độ dài cạnh đáy của hình chóp đó là
\({\rm{50}}\;{\rm{cm}}\).
\({\rm{5}}\;{\rm{cm}}\).
\[{\rm{25}}\;{\rm{cm}}\].
\({\rm{5}}\;{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Rút gọn các biểu thức sau:
a) \(A = {x^2}\left( {x - {y^2}} \right) - xy\left( {1 - yx} \right) - {x^3}\).
b) \(B = x\left( {x + 3y + 1} \right) - 2y\left( {x - 1} \right) - \left( {y + x + 1} \right)x\).
Cho các đa thức \(A = 4{x^2} + 3{y^2} - 5xy\); \(B = 3{x^2} + 2{y^2} + 2{x^2}{y^2}\). Tìm đa thức \(C\) sao cho
a) \(C = A + B\). b) \(C + A = B\).
Phân tích các đa thức sau thành nhân tử:
a) \(36x{y^3} - 12{x^2}{y^2}\); b) \({x^2} - x + \frac{1}{4}\); c) \[{a^2}x + {a^2}y - 7x - 7y.\]
Cho biểu thức: \(E = \left( {\frac{1}{{x + 2}} + \frac{1}{{x - 2}}} \right) \cdot \frac{{{x^2} + 4x + 4}}{{2x}}\).
a) Viết điều kiện xác định của biểu thức \[E\].
b) Rút gọn biểu thức \[E\].
Cho một hình chóp tứ giác đều \[S.ABCD\] có diện tích đáy là \(400\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\), trung đoạn \[SI = 25\,\,{\rm{cm}}.\] Tính diện tích xung quanh và diện tích toàn phần (tức là tổng diện tích các mặt) của hình chóp tứ giác đều \[S.ABCD\].
![Cho một hình chóp tứ giác đều [S.ABCD] có diện tích đáy là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/blobid3-1763434580.png)
Cho biểu thức \(Q = (2n - 1)(2n + 3) - (4n - 5)(n + 1) + 3\). Chứng minh \(Q\) luôn chia hết cho \(5\) với mọi số nguyên \(n\).








