Bộ 10 đề thi giữa kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 4
37 câu hỏi
Biểu thức nào không phảilà đa thức trong các biểu thức sau?
\(2{x^2}y + 3 + xy\).
\(\frac{{x + y}}{2}\).
\(2 - \frac{{x + 1}}{{x - 1}}\).
\(x\left( {x + 2y} \right)\).
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3{x^2}y\)?
\(3{x^2}yz\).
\(\frac{1}{2}xyx\).
\(x{y^2}\).
\( - 3{x^2}z\).
Tích của đa thức \[6xy\]và đa thức \[2{x^2} - 3y\]là đa thức
\[12{x^2}y + 18x{y^2}\].
\[12{x^3}y - 18x{y^2}\].
\[12{x^3}y + 18x{y^2}\].
\[12{x^2}y - 18x{y^2}\].
Hệ số của \[{x^4}\] trong đa thức \[A = \left( {{x^3} - 2{x^2} + x - 1} \right)\left( {5{x^3} - x} \right)\]là
\[4\].
\[ - 4\].
\[ - 6\].
\[6\].
Hằng đẳng thức bình phương của một hiệu là
\[{\left( {A + B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B - {B^2}\].
Khai triển của \({x^3} - 27\) là
\(\left( {x - 3} \right)\left( {{x^2} - 3x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} + 6x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} - 6x + 9} \right)\).
Chiếc hộp bánh ít trong hình bên có dạng hình gì? 
Hình lăng trụ đứng tam giác.
Hình chóp tam giác đều.
Hình chóp tứ giác đều.
Hình tam giác.
Cho hình chóp tam giác đều \[A.BCD\](như hình vẽ bên). Trung đoạn của hình chóp là đoạn thẳng
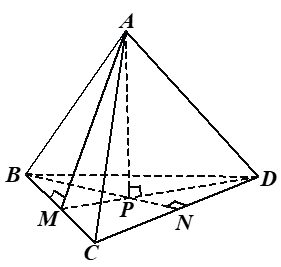
\[AM.\]
\[AC.\]
\[BN.\]
\[AP.\]
Hình chóp tam giác đều và hình chóp tứ giác đều có chung đặc điểm nào sau đây?
Đáy là tam giác đều.
Đáy là hình vuông.
Các cạnh bên bằng nhau.
Mặt bên là các tam giác đều.
Cho hình chóp tam giác đều \(S.ABC\) có đường cao \(SO\) (như hình vẽ). Các cạnh bên của hình chóptam giác đều là 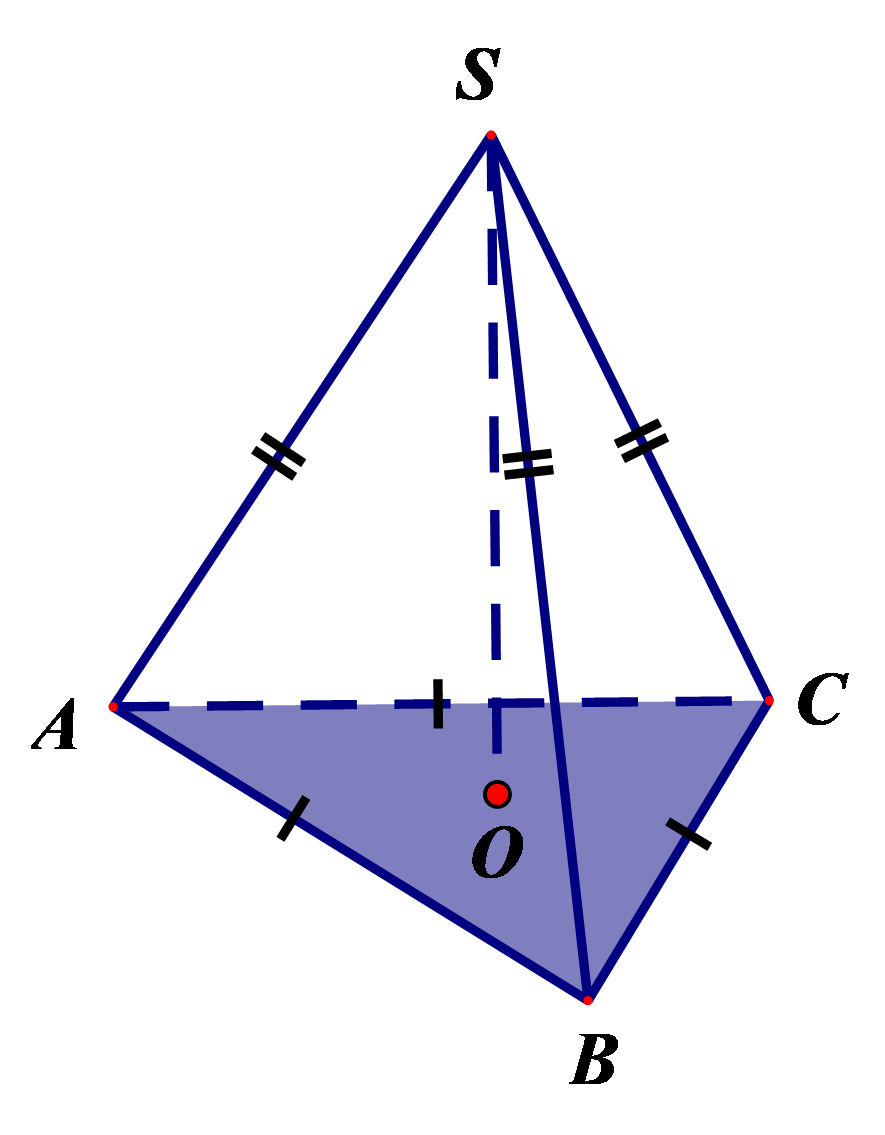
\(AB,\,\,BC,\,\,AC\).
\(SA,\,\,SB,\,\,SC,\,\,SO\).
\(SA,\,\,SB,\,\,SC\).
\(SAB,\,\,SBC,\,\,SAC\).
Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AH.\) Cho \(AH = 4\;\;{\rm{cm}},\,\,AB = 5\;\;{\rm{cm}}.\) Chu vi tam giác \(ABC\) bằng
\(16\;\;{\rm{cm}}\).
\(18\;\;{\rm{cm}}\).
\(12\;\;{\rm{cm}}\).
\(15\;\;{\rm{cm}}\).
Khẳng định nào sau đây là đúng?
Tứ giác có 4 đường chéo.
Tổng các góc của một tứ giác bằng .
Tồn tại một tứ giác có 1 góc tù và 3 góc vuông.
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)
Đa thức \(M\) và \(P\) thỏa mãn \(B = A + M\,;\, & P = \left( {x - 3} \right)M - y - \left( {x + y} \right)\left( {xy - 3y} \right).\)
a) Hạng tử tự do của đa thức \(A\) là \( - 4\).
b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)
c) \(M = {x^2} + 7xy + {y^2}.\)
d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60{\rm{ cm}}\) và \(30{\rm{ cm}}{\rm{.}}\) Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270{\rm{ c}}{{\rm{m}}^2}\), chiều cao \(30{\rm{ cm}}{\rm{.}}\) Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là \(60{\rm{ cm}}{\rm{.}}\)
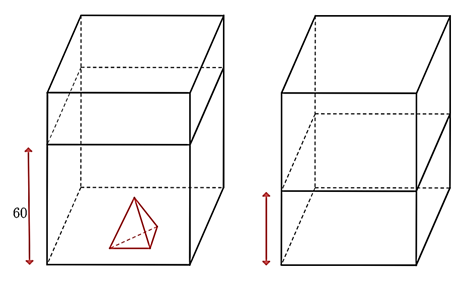
a) Diện tích đáy của bể hình hộp chữ nhật là \(180{\rm{ c}}{{\rm{m}}^{\rm{2}}}\).
b) Thể tích khối đá hình chóp tam giác đều là \(2{\rm{ }}700{\rm{ c}}{{\rm{m}}^3}.\)
c) Thể tích khối nước là\(108{\rm{ }}000{\rm{ c}}{{\rm{m}}^2}\).
d) Khi lấy khối đá ra thì mực nước của bể cao 56 cm.
Xác định phần hệ số của tích của hai đơn thức \(\frac{1}{2}x{y^3}\) và \(x\left( { - 8y} \right)x{z^2}\).
Giá trị của biểu thức \[A = {\left( {3x + 1} \right)^2} + {\left( {3x--1} \right)^2}--2\left( {3x--1} \right)\left( {3x + 1} \right)\] bằng bao nhiêu?
Nhà bạn Vân có một đèn trang trí có dạng hình chóp tam giác đều (như hình vẽ). Các cạnh của hình chóp đều bằng nhau và bằng \(20{\rm{ cm}}\). Bạn Vân dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.
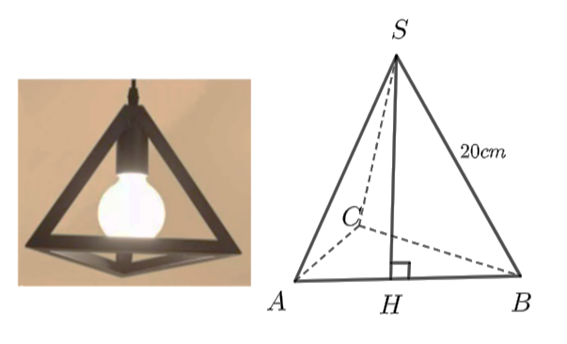
Tính diện tích giấy màu mà bạn Vân sử dụng (coi như mép dán không đáng kể)(kết quả làm tròn đến hàng đơn vị với đơn vị \({\rm{c}}{{\rm{m}}^2}\)).
Cho tứ giác \[ABCD\] có \(\widehat A = 50^\circ \,;\,\,\widehat B = 130^\circ \,;\,\,\widehat C = 80^\circ \). Tính số đo của \(\widehat D\) (đơn vị: độ).
![Cho tứ giác \[ABCD\] có \(\widehat A = 50^\circ \,;\,\,\widehat B = 130^\circ \,;\,\,\widehat C = 80^\circ \). Tính số đo của \(\widehat D\) (đơn vị: độ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid3-1750301801.png)
Phân tích các đa thức sau thành nhân tử:
a) \[10{x^2}\left( {2x - y} \right) + 6xy\left( {y - 2x} \right)\]. b) \[\frac{{{x^3}}}{8} - \frac{{{y^3}}}{{27}} + \frac{x}{2} - \frac{y}{3}\]. c) \({x^3} + 27 + \left( {x + 3} \right)\left( {x - 9} \right)\).
1. Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\), điện thoại có chiều rộng là \[7\,\,{\rm{cm;}}\] chiều dài là \[15,5{\rm{ cm}}.\] Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị) 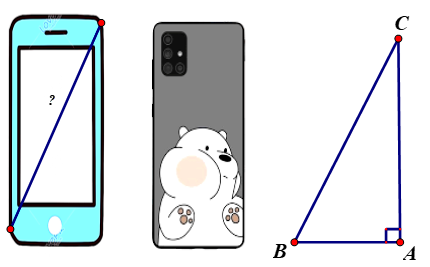
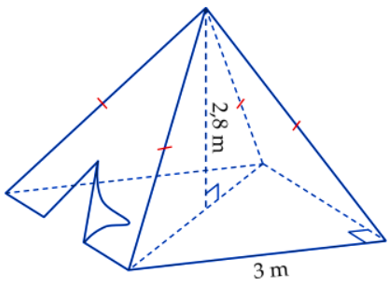
2. Một chiếc lều ở trại hè cho học sinh có dạng hình chóp tứ giác đều với chiều cao bằng \[2,8\,\,{\rm{m}};\] độ dài cạnh đáy bằng \[3\,{\rm{m}}\,{\rm{.}}\]
a) Tính thể tích không khí bên trong của chiếc lều.
b) Người ta muốn sơn phủ bên ngoài cả bốn mặt xung quanh của lều và không sơn phủ phần làm cửa có diện tích là\[5\,\,{{\rm{m}}^2}.\] Biết độ dài trung đoạn của lều là \[3,18\,\,{\rm{m}}\]và cứ mỗi mét vuông sơn cần trả \[35\,\,000\] đồng. Tính số tiền cần phải trả để hoàn thành việc sơn phủ cho lều.
Trong các biểu thức đại số sau, biểu thức nào không phải là đa thức?
\(x + 5\).
\(2xy\).
\(\frac{3}{x} + 1\).
\(\frac{x}{3} - 2\).
Thực hiện phép tính nhân \({x^2}\left( {5{x^3} - x - \frac{1}{2}} \right)\) ta được kết quả
\(5{x^6} - {x^3} - \frac{1}{2}{x^2}\).
\[5{x^5} - {x^3} - \frac{1}{2}{x^2}\].
\[5{x^5} - {x^3} - \frac{1}{2}\].
\[5{x^6} - {x^2} - \frac{1}{2}{x^2}\].
Kết quả của phép chia \(\left[ {{{\left( {x - y} \right)}^3} - {{\left( {x - y} \right)}^2} + \left( {x - y} \right)} \right]:\left( {y - x} \right)\) là
\({\left( {x - y} \right)^2} - \left( {x - y} \right) + 1\).
\( - {\left( {x - y} \right)^2} + \left( {x - y} \right) + 1\).
\({\left( {x - y} \right)^2} + \left( {x - y} \right) + 1\).
\( - {\left( {x - y} \right)^2} + \left( {x - y} \right) - 1\).
Điền vào chỗ trống sau: .
\[2x\].
\[4x\].
\[2\].
\[4\].
Chọn phương án sai.
\({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\).
\({\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\).
\({\left( { - a + b} \right)^3} = - {a^3} - 3{a^2}b + 3a{b^2} + {b^3}\).
\({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\).
Phân thức \[\frac{A}{B}\] xác định khi
\(B \ne 0\).
\(B \ge 0\).
\(B \le 0\).
\(A = 0\).
Phép tính \(\frac{2}{{x + 3}} - \frac{{ - 6}}{{{x^2} + 3x}}\) có kết quả là
\[\frac{2}{x}\].
\[\frac{2}{{x + 3}}\].
\[\frac{{2x}}{{x + 3}}\].
\[\frac{2}{{x\left( {x + 3} \right)}}\].
Cho \(\frac{{5x + 2}}{{3x{y^2}}} \cdot \frac{{{x^2}y}}{{10x + 4}} = \frac{{...}}{{6y}}\). Đa thức thích hợp điền vào chỗ trống là
\[xy\].
\[{x^2}y\].
\[{x^2}\].
\[x\].
Hình chóp tứ giác đều là hình chóp có đáy là hình gì?
Hình chữ nhật.
Hình bình hành.
Hình vuông.
Hình thoi.
Cho hình chóp tứ giác đều \(S.ABCD\) (như hình vẽ). Khi đó đường cao của hình chóp là
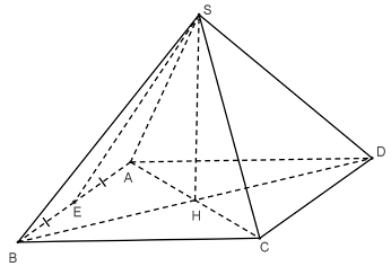
\[SA\].
\[SE\].
\[SC\].
\[SH\].
Tính chiều cao của hình chóp tam giác đều có cạnh đáy là \[a\] và thể tích bằng \[\frac{{{a^3}\sqrt 3 }}{8}\] là
\[h = 3a\].
\[h = \frac{{3a}}{2}\].
\[h = \frac{{3a}}{4}\].
\[h = \frac{{3a}}{8}\].
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh bằng \[3\,\,{\rm{cm}}{\rm{,}}\] chiều cao của hình chóp là \[h = 2\,\,{\rm{cm}}.\] Thể tích của hình chóp đã cho là
\[6\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[18\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[12\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[9\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
Tìm biểu thức \(M,\,\,N\), biết:
a) \(M - \left( {2{\rm{x}}y - 4{y^2}} \right) = 5{\rm{x}}y + {x^2} - 7{y^2}.\)
b) \(2{x^2}y - {x^3} - x{y^2} + 1 = N - \left( {{x^3} + 2x{y^2} - 2} \right)\).
Phân tích các đa thức sau thành nhân tử:
a) \[4x\left( {x - 2y} \right) - 8y\left( {x - 2y} \right)\];
b) \( - 25{x^2}{y^2} + 10xy - 1\);
c) \[{x^3} + {x^2} + xy - {y^3} + {y^2}.\]
Cho biểu thức: \(B = \frac{2}{{{x^2} - 5x + 6}}:\frac{{x + 2}}{{x - 2}}\) với \[x \ne \pm \,2;\,\,x \ne 3.\]
\a) Rút gọn biểu thức \(B\).
b) Tính giá trị biểu thức \(B\) khi \(x = 5\).
Cho hình chóp tứ giác đều \[S.MNPQ\] như hình vẽ bên có chiều cao \[15\,\,{\rm{cm}}\] và thể tích là \[1\,\,280{\rm{ c}}{{\rm{m}}^{\rm{3}}}{\rm{.}}\]
a) Tính độ dài cạnh đáy của hình chóp.
b) Tính diện tích xung quanh của hình chóp biết, độ dài trung đoạn của hình chóp là \[17\,\,{\rm{cm}}.\]
![Cho hình chóp tứ giác đều [S.MNPQ] như hình vẽ bên có chiều cao (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/blobid1-1763433178.png)
Cho \({a^2} + {b^2} + {c^2} = ab + bc + ca.\) Chứng minh rằng: \(a = b = c.\)








