Bộ 10 đề thi giữa kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 3
37 câu hỏi
Bậc của đa thức \({x^2}{y^5} - {x^2}{y^4} + {y^6} + 1\) là
\[4\].
\(5\).
\(6\).
\(7\).
Khi nhân đa thức \(M + N\) với đa thức \(P\)ta được kết quả là
\[MP + NP\].
\[MP + N\].
\[MN + NP\].
\[M + NP\].
Cặp đơn thức nào sau đây không đồng dạng?
\(7{x^3}y\) và \(\frac{1}{{15}}{x^3}y\).
\( - \frac{1}{8}{\left( {xy} \right)^2}{x^2}\) và \(32{x^2}{y^3}\).
\(5{x^2}{y^2}\) và \( - 2{x^2}{y^2}\).
\(a{x^2}y\) và \(2b{x^2}y\)\((a,b\) là các hằng số khác \(0).\)
Cho biểu thức \(H = \left( {2x - 3} \right)\left( {x + 7} \right) - 2x\left( {x + 5} \right) - x\). Khẳng định nào sau đây là đúng?
\(H = 21 - x\).
\(H > 0\).
\(H < - 1\).
\(10 < H < 20\).
Điền vào chỗ trống sau: .
\(2x\).
\(4x\).
\(2\).
\(4\).
Kết quả phân tích đa thức \(6{x^2}y - 12x{y^2}\) là
\(6xy\left( {x + y} \right)\).
\(6xy\left( {x - y} \right)\).
\(6xy\left( {x + 2y} \right)\).
\(6xy\left( {x - 2y} \right)\).
Cho các miếng bìa sau:
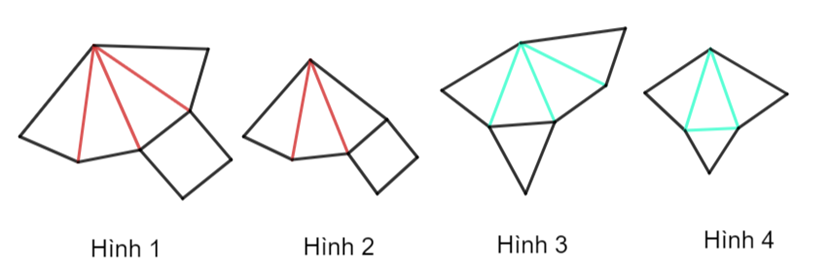
Miếng bìa nào sau khi gấp và dán lại thì được một hình chóp tứ giác đều?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đường cao của hình chóp tam giác đều là
Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy.
Đoạn thẳng nối đỉnh của hình chóp và trung điểm của một cạnh đáy.
Đoạn thẳng nối đỉnh của hình chóp và một điểm tùy ý nằm trong mặt đáy.
Đoạn thẳng nối đỉnh của hình chóp và một điểm bất kì trên cạnh bên của hình chóp.
Diện tích xung quanh của hình chóp \(S.ABCD\) (hình bên) gồm diện tích những mặt nào?
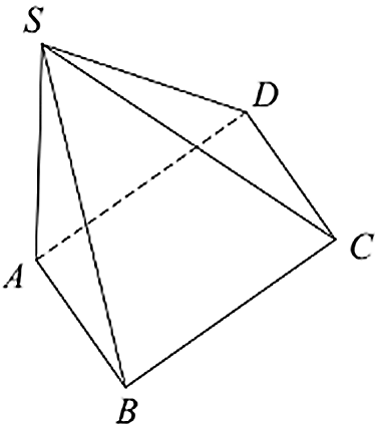
Mặt \(SBC,\,\,ABCD,\,\,SAB\).
Mặt \(SAB,\,\,SBC,\,\,SCD,\,\,SDA\).
Mặt \(SAB,\,\,SAD,\,\,SBC,\,\,ABCD\).
Mặt \(ABCD\).
Thể tích của hình chóp tam giác đều bằng
diện tích đáy nhân với chiều cao.
\(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(\frac{1}{2}\) chiều cao nhân với diện tích đáy.
\(\frac{3}{2}\) diện tích đáy nhân với chiều cao.
Độ dài cạnh \(BC\) trong \(\Delta ABC\) cân tại \(A\)ở hình vẽ bên là 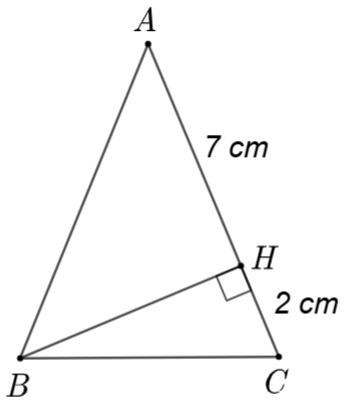
\(4\;\;{\rm{cm}}\).
\(5\;\;{\rm{cm}}\).
\(6\;\;{\rm{cm}}\).
\(7\;\;{\rm{cm}}\).
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
\(AB\) và \(BC\) là hai cạnh kề nhau.
\(BC\) và \(AD\) là hai cạnh đối nhau.
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau.
\(AC\) và \(BD\) là hai đường chéo.
Cho hai biểu thức \(A\) và \(B\) thỏa mãn \(45{x^6}{y^3}:A = 5{x^3}{y^2}\) và \(\left( {B + 7{x^4}{y^2}} \right):A = 3x{y^2} + 2xy.\)
a) Biểu thức \(A\) là đơn thức bậc 3.
b) Với \(x = - 1\,;\,\,y = 2\) thì giá trị của biểu thức \(A\) bằng \( - 18.\)
c) Đa thức \(B\) có hai hạng tử.
d) Tích của hai biểu thức \(A\) và \(B\) là \(36{x^7}{y^5} + 20{x^7}{y^3}.\)
Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2 m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn tất cả các mặt của hộp gỗ. Cứ mỗi mét vuông sơn cần trả \[30\,\,000\] đồng (tiền sơn và tiền công).
a) Diện tích mặt đáy hộp gỗ là \(4\,\,{{\rm{m}}^{\rm{2}}}\).
b) Diện tích xung quanh của khối gỗ là \(24\,\,{{\rm{m}}^{\rm{2}}}\).
![Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2 m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn tất cả các mặt của hộp gỗ. Cứ mỗi mét vuông sơn cần trả \[30\,\,000\] đồng (tiền sơn và tiền công). a) Diện tích mặt đáy hộp gỗ là \(4\,\,{{\rm{m}}^{\rm{2}}}\). b) Diện tích xung quanh của khối gỗ là \(24\,\,{{\rm{m}}^{\rm{2}}}\). c) Diện tích cần sơn là \(16{\rm{ }}{{\rm{m}}^2}\). d) Chi phí bác Khôi cần phải trả là \(420\,\,000\) đồng. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid1-1750300763.png)
c) Diện tích cần sơn là\(16{\rm{ }}{{\rm{m}}^2}\).
d) Chi phí bác Khôi cần phải trả là \(420\,\,000\)đồng.
Cho \(B - \left( {5{x^2} - 2xyz} \right) = 2{x^2} + 2xyz + 1\). Hạng tử tự do của đa thức \(B\) là bao nhiêu?
Để biểu thức \[{x^3} + 6{x^2} + 12x + m\] là lập phương của một tổng thì giá trị của\(m\) là bao nhiêu?
Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
![Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid2-1750300843.png)
Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\].
![Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\]. Tính số đo \[\widehat {{C_1}}\] (đơn vị: độ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid3-1750300873.png)
Tính số đo \[\widehat {{C_1}}\] (đơn vị: độ).
Tìm \(x\), biết:
a) \[{x^3} + 9{x^2} + 27x + 19 = 0\];
b) \[25{\left( {x + 3} \right)^2} + \left( {1--5x} \right)\left( {1 + 5x} \right) = 8\];
c) \[3{\left( {x + 2} \right)^2} + {\left( {2x - 1} \right)^2} - 7\left( {x + 3} \right)\left( {x - 3} \right) = 36\].
1.Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\]đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\]Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\)(xem hình vẽ).Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\]có “an toàn” không?![1. Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\] Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\) (xem hình vẽ). Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\] có “an toàn” không? 2. Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\) (Làm tròn các kết quả đến chữ số thập phân thứ hai) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid5-1750300979.png)
2.Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên).Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\)
(Làm tròn các kết quả đến chữ số thập phân thứ hai)
![1. Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\] Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\) (xem hình vẽ). Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\] có “an toàn” không? 2. Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\) (Làm tròn các kết quả đến chữ số thập phân thứ hai) (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid6-1750300990.png)
Trong các biểu thức đại số sau, biểu thức nào không phải là đơn thức?
\(5x + 9\).
\({x^3}{y^2}\).
2.
\(x\).
Thực hiện phép tính nhân \[\left( {x - 1} \right)\left( {x + 3} \right)\] ta được kết quả
\[{x^2} - 3\].
\[{x^2} + 3\].
\[{x^2} + 2x - 3\].
\[{x^2} - 4x + 3\].
Kết quả phép tính \(\left( {12{x^3}{y^4} + 8{x^4}{y^2}} \right):{\left( {2xy} \right)^2}\) là
\(6{x^2}{y^3} + 2{x^3}y\).
\(3{x^2}{y^3} + 2{x^3}y\).
\(3x{y^2} + 2{x^2}y\).
\(3x{y^2} + 2{x^2}\).
Hằng đẳng thức \[{\left( {A + B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\] có tên là
bình phương của một tổng.
tổng hai bình phương.
bình phương của một hiệu.
hiệu hai bình phương
Giá trị \[x\] thỏa mãn \[4{x^2} + 12x + 9 = 0\] là
\[x = \frac{3}{2}\]
\[x = - \frac{3}{2}\].
\[x = \frac{2}{3}\].
\[x = - \frac{2}{3}\].
Với điều kiện nào của \[x\] thì phân thức \(\frac{{{{(x - 1)}^3}}}{{(x - 2)(x + 3)}}\) có nghĩa?
\[x \le 2\].
\(x \ne 2;\,\,x \ne - 3\).
\[x = 2\].
\[x \ne 2\].
Kết quả của phép tính \(\frac{{2 + x}}{{3{x^2}y}} + \frac{{1 - y}}{{3x{y^2}}}\) là
\[\frac{{2y - x}}{{3{x^2}{y^2}}}\].
\[\frac{{2y + x}}{{3{x^2}{y^2}}}\].
\[\frac{{2y + x}}{{9{x^2}{y^2}}}\].
\[\frac{{2y - x}}{{9{x^2}{y^2}}}\].
Biết \(\frac{{x + 3}}{{{x^2} - 4}} \cdot \frac{{{{\left( {2 - x} \right)}^3}}}{{9x + 27}} = \frac{{...}}{9}\). Điền kết quả thích hợp vào chỗ trống.
\[\frac{{x - 2}}{{x + 2}}\].
\[\frac{{{{\left( {x - 2} \right)}^2}}}{{x + 2}}\].
\[\frac{{x + 2}}{{{{\left( {x - 2} \right)}^2}}}\,\].
\[\frac{{ - {{\left( {x - 2} \right)}^2}}}{{x + 2}}\].
Hình chóp tam giác đều có bao nhiêu mặt?
3.
5.
6.
4.
Cuốn lịch để bàn trong hình bên có dạng hình gì?
Hình lăng trụ đứng tam giác.
Hình chóp tam giác đều.
Hình chóp tứ giác đều.
Hình tam giác.
Cho hình chóp tam giác đều có độ dài đáy bằng 4 cm và độ dài trung đoạn bằng 6 cm. Diện tích xung quanh của hình chóp tam giác đều này bằng
\[12\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
\[18\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
\[72\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
\[36\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
Một hộp quà lưu niệm có dạng hình chóp tứ giác đều với độ dài đáy là 7 cm và chiều cao là 6 cm. Thể tích của hộp quà lưu niệm là

\[98\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[42\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[21\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[14\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
Thực hiện phép tính:
a) \(\left( {{x^2}y + {x^3} - x{y^2} + 3} \right) + \left( {{x^3} + x{y^2} - xy - 6} \right)\). b) \(2{x^2}{y^2}\left( {{x^3}{y^2} - {x^2}{y^3} - \frac{1}{2}{y^5}} \right)\).
c) \((3{x^3} - {x^2}y + 2xy + 3) - (3{x^3} - 2{x^2}y - xy + 3)\). d) \(\left[ {{{\left( {3ab} \right)}^2} - 9{a^2}{b^4}} \right]:\left( {8a{b^2}} \right)\).
Phân tích các đa thức sau thành nhân tử:
a) \(48{x^3}{y^3} - 32{x^2}{y^2}\); b) \(9{x^2} - 6x + 1\); c) \[{x^3} - 9x + 2{x^2}y + x{y^2}.\]
Cho phân thức: \(A = \frac{{{x^2} - 4}}{{\left( {x - 3} \right)\left( {x - 2} \right)}}\).
a) Tìm điều kiện của \[x\] để giá trị của phân thức được xác định.
b) Rút gọn phân thức \[A\].
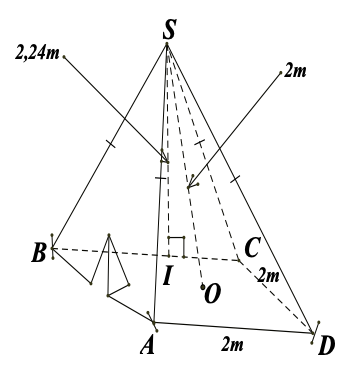
Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ.
a) Thể tích không khí bên trong lều là bao nhiêu?
b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, …) là bao nhiêu? Biết độ dài trung đoạn của lều trại là \[2,24{\rm{ m}}.\]
Cho biểu thức \(M = {\left( {x - 3} \right)^3} + {\left( { - x - 1} \right)^3}\). Tính giá trị lớn nhất của biểu thức \(M.\)








