Bộ 10 đề thi giữa kì 1 Toán 8 Chân trời sáng tạo có đáp án - Đề 3
39 câu hỏi
Trong các biểu thức đại số sau, biểu thức nào là đơn thức?
\(\frac{{2x}}{y}\).
\(3x + 2y\).
\(4\left( {x - y} \right)\).
\( - \frac{2}{3}x{y^2}\).
Cho đơn thức \({3^2}{x^2}{y^4}\). Đơn thức nào dưới đây đồng dạng với đơn thức đã cho?
\( - {3^2}{x^4}{y^2}\).
\(7{x^2}{y^4}\).
\(\frac{1}{3}{x^6}\).
\( - 9{x^4}{y^6}\).
Kết quả của phép chia \(5{x^2}{y^5}:10{x^2}{y^3}\) là
\({y^4}\).
\(\frac{1}{2}x{y^3}\).
\(50{x^4}{y^8}\).
\(\frac{1}{2}{y^2}\).
Thu gọn đa thức \(Q = {x^2} + {y^2} + {z^2} + {x^2} - {y^2} + {z^2} + {x^2} + {y^2} - {z^2}\) được kết quả là
\(Q = 3{x^2} + 3{y^2} + 3{z^2}\).
\(Q = {x^2} + {y^2} + {z^2}\).
\(Q = 3{x^2} + {y^2} + {z^2}\).
\(Q = 3{x^2} - {y^2} - {z^2}\).
Khẳng định nào sau đây là sai?
\({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\).
\({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\).
\({x^3} - {y^3} = \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\).
\({\left( {x - y} \right)^3} = {x^3} - {y^3}\).
Cho \({x^3} + 12{x^2} + 48x + 64 = {\left( {x + a} \right)^3}\). Giá trị của \(a\) là
4.
64.
\( - 4\).
\( - 64\).
Cho các hình dưới đây.

Hình có dạng là hình chóp tam giác đều là
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Diện tích xung quanh của hình chóp tam giác đều là
nửa chu vi đáy nhân với đường cao.
chu vi đáy nhân với trung đoạn.
nửa chu vi đáy nhân với trung đoạn.
chu vi đáy nhân với chiều cao.
Hình chóp tứ giác đều có đáy là
hình thoi.
tam giác đều.
hình vuông.
tam giác.
Một hình chóp tứ giác đều có diện tích xung quanh \({S_{xq}}\) và chiều cao \(h\). Khi đó nửa chu vi đáy là
\(\frac{{2{S_{xq}}}}{h}\).
\(\frac{{{S_{xq}}}}{h}\).
\(\frac{{{S_{xq}}}}{{2h}}\).
\(\frac{{2h}}{{{S_{xq}}}}\).
Một cây cao \[12\,\,{\rm{m}}\]mọc cạnh bờ sông. Trên đỉnh cây có một con chim đang đậu và chuẩn bị sà xuống bắt con cá trên mặt nước (như Hình 1 và được mô phỏng như Hình 2). Hỏi con chim sẽ bay một đoạn ngắn nhất bằng bao nhiêu mét thì bắt được con cá? (Biết con cá cách gốc cây \[5\,\,{\rm{m}}\] và nước cao mấp mé bờ sông). 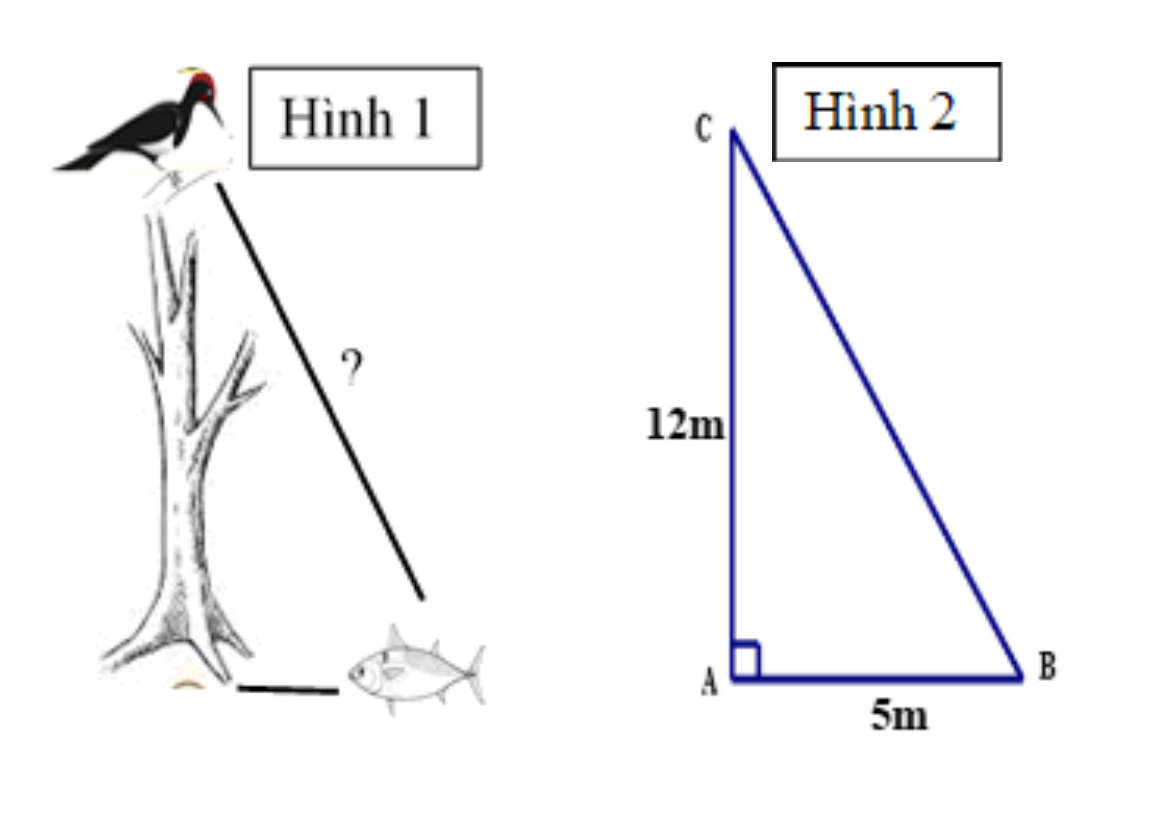
\(12\;\;{\rm{cm}}\).
\(13\,\;{\rm{cm}}\).
\(15\;\;{\rm{cm}}\).
\(18\;\;{\rm{cm}}\).
Cho hình vẽ bên. Khẳng định nào sau đây là sai?
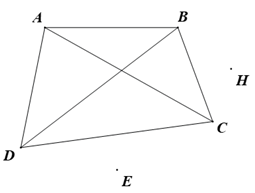
Hai cạnh \(AB\)và \[BC\] kề nhau.
Hai cạnh \[BC\] và \[DA\] đối nhau.
Các cặp góc \[\widehat A\] và \[\widehat B\,;\,\,\widehat C\] và \[\widehat D\]đối nhau.
Các điểm \[H\] và \[E\]nằm ngoài.
Cho hai đa thức \(P = {x^2} - 4xy + 9\) và \(Q = - 6xy - 4{y^2} + 9.\)
Đa thức \(A\) và \(M\) thỏa mãn \(P - A = Q\,;\, & M = \left( {x - 2y} \right)A - {x^3} + 5.\)
a) Với \(x = 1\,;\,\,y = - 1\) thì giá trị của biểu thức \(P\) bằng 10.
b) Đa thức \(Q\) có bậc là 2.
c) \[A = {x^2} + xy + 4{y^2}.\]
d) Giá trị của biểu thức \(M\) không phụ thuộc vào biến \(x.\)
Bạn Như làm một cái lòng đèn hình quả trám (như hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy \[20\,\,{\rm{cm}}\], cạnh bên \[32\,\,{\rm{cm}}\,{\rm{,}}\] khoảng cách giữa hai đỉnh của hai hình chóp là \[30\,\,{\rm{cm}}.\]
a)Công thức tính thể tích hình chóp tứ giác đều: \(V = S \cdot h.\)
Trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều).
b) Chiều cao của mỗi hình chóp tứ giác đều là 15 cm.
c) Thể tích của lồng đèn là \(4\,\,000\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\)
d) Bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị 165 mét thanh tre? (mối nối giữa các que tre có độ dài không đáng kể).
![Bạn Như làm một cái lòng đèn hình quả trám (như hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy \[20\,\,{\rm{cm}}\], cạnh bên \[32\,\,{\rm{cm}}\,{\rm{,}}\] khoảng cách giữa hai đỉnh của hai hình chóp là \[30\,\,{\rm{cm}}.\] a) Công thức tính thể tích hình chóp tứ giác đều: \(V = S \cdot h.\) Trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều). b) Chiều cao của mỗi hình chóp tứ giác đều là 15 cm. c) Thể tích của lồng đèn là \(4\,\,000\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\) d) Bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị 165 mét thanh tre? (mối nối giữa các que tre có độ dài không đáng kể). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid2-1750299514.png)
Kết quả của phép chia \(\left( {5{x^5}{y^4}z + \frac{1}{2}{x^4}{y^2}{z^3} - 2x{y^3}{z^2}} \right):\frac{1}{4}x{y^2}z\) là đa thức bậc mấy?
Có bao nhiêu giá trị \(x\) thỏa mãn \[12{x^3}--27x = 0\]?
Cho hình hộp chữ nhật có các kích thước như hình vẽ.
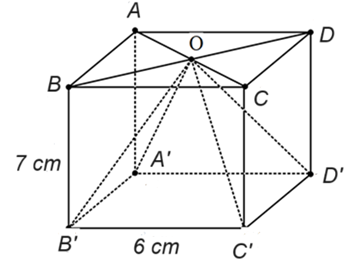
Tính thể tích hình chóp tam giác đều\(O.A'B'C'D'\) (đơn vị: \({\rm{c}}{{\rm{m}}^{\rm{3}}}).\)
Cho hình vẽ dưới đây. Tính số đo góc \(A\) (đơn vị: độ).
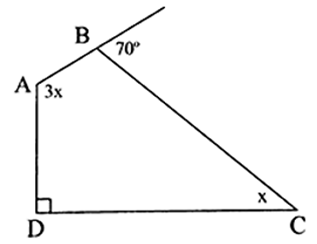
Phân tích các đa thức sau thành nhân tử:
a) \[10{x^2}\left( {2x - y} \right) + 6xy\left( {y - 2x} \right)\]. b) \[\frac{{{x^3}}}{8} - \frac{{{y^3}}}{{27}} + \frac{x}{2} - \frac{y}{3}\]. c) \({x^3} + 27 + \left( {x + 3} \right)\left( {x - 9} \right)\).
1.Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\]\[(A\]là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\]nếu \[BC = 5\,\,{\rm{cm}}\]thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?![1. Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\] \[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\,\,{\rm{cm}}\] thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao? 2. Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm}}{\rm{,}}\) chiều cao \({\rm{2}}{\rm{,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid6-1750299828.png)
2. Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm}}{\rm{,}}\) chiều cao \({\rm{2}}{\rm{,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\)
![1. Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\] \[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\,\,{\rm{cm}}\] thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao? 2. Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm}}{\rm{,}}\) chiều cao \({\rm{2}}{\rm{,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\) (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid7-1750299845.png)
Trong các biểu thức đại số sau, biểu thức nào là đa thức?
\( - x{y^2}\).
\(\frac{1}{3}\).
\(x\).
\(4{x^2}y + 5\).
Kết quả của phép nhân \[ - \frac{3}{4}x\left( {4x - 8} \right)\] là
\[ - 3{x^2} + 6x\].
\[ - 3{x^2} - 6x\].
\[3{x^2} + 6x\].
\[3{x^2} - 6x\].
Kết quả phép chia đa thức \( - 2{x^3}{y^2}z + 8{x^2}{y^3}{z^2} - 10{x^4}y{z^2}\) cho đơn thức \( - 2xyz\) là
\({x^2}y - 4x{y^2}z + 5{x^2}z\).
\({x^2}y - 4xyz + 5{x^3}z\).
\({x^2}y - 4x{y^2}z + 5{x^3}z\).
\({x^2}y - 4x{y^2}z + 5x{z^3}\).
Hằng đẳng thức bình phương của một hiệu là
\[{\left( {A + B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B - {B^2}\].
Rút gọn biểu thức \[A = {\left( {a + b} \right)^3} + {\left( {a - b} \right)^3} - 6a{b^2}\], ta thu được
\[2{b^3}\].
\[2{a^3}\].
\[ - 2{b^3}\].
\[ - 2{a^3}\].
Mẫu thức chung của hai phân thức \(\frac{{3x}}{{{x^2} - 4}}\) và \(\frac{x}{{x + 2}}\) là
\[{x^2} - 4\].
\[x + 2\].
\[x - 2\].
\[\left( {{x^2} - 4} \right)\left( {x + 2} \right)\].
Kết quả phép tính \(\frac{{2y - 1}}{y} - \frac{{2x + 1}}{x}\) là
\[\frac{{ - 1}}{{xy}}\].
\[\frac{{x + y}}{{xy}}\].
\[\frac{{x - y}}{{xy}}\].
\[\frac{{ - x - y}}{{xy}}\].
Cho biểu thức \(M = \frac{{x + 4}}{5} \cdot \frac{{x + 1}}{{2x}} \cdot \frac{{100x}}{{\left( {x + 1} \right)\left( {x + 4} \right)}}\). Rút gọn biểu thức\(M\), ta được
\[M = 100\].
\[M = 12\].
\[M = 10\].
\[M = 1\].
Một hình chóp tam giác đều và một hình lăng trụ đứng tam giác đều có cùng chiều cao. Nếu thể tích của hình lăng trụ là \[V\] thì thể tích của hình chóp là
\[V\].
\[\frac{1}{3}V\].
\[\frac{1}{2}V\].
\[3V\].
Kim tự tháp Ai Cập có dạng hình gì?

Hình lăng trụ đứng tam giác.
Hình chóp tam giác đều.
Hình chóp tứ giác đều.
Hình tam giác.
Một hình chóp tam giác đều có diện tích xung quanh là \[{\rm{20}}\,c{m^2}\], chu vi đáy là \[{\rm{10}}\,{\mathop{\rm cm}\nolimits} \]. Trung đoạn của hình chóp là
\[{\rm{4}}\,\,{\mathop{\rm cm}\nolimits} \].
\[{\rm{2}}\,\,{\mathop{\rm cm}\nolimits} \].
\[{\rm{0}}{\rm{,5}}\,\,cm\].
\[{\rm{3}}\,\,{\mathop{\rm cm}\nolimits} \].
Một kim tử tháp pha lê đen có dạng hình chóp tứ giác đều biết, độ dài cạnh đáy là \[8,5\,\,{\rm{cm}}{\rm{,}}\] chiều cao là \[9,5\,\,{\rm{cm}}.\] Tính thể tích của kim tự tháp pha lê đen đó (làm tròn kết quả đến hàng phần mười).

\[228,8\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[26,92\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\]
\[40,38\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
\[343,19\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\].
Cho \(\left( {6{{\rm{x}}^2} - 3{\rm{x}}{y^2}} \right) + M = {x^2} + {y^2} - 2{\rm{x}}{y^2}\). Tìm biểu thức \(M.\)
Thực hiện phép tính:
a) \({\left( { - x{y^2}} \right)^2} \cdot \left( {{x^2} - 2x + 1} \right)\).
b) \(\left( {x + 2y} \right)\left( {{x^2} - 2y + 4z} \right)\).
c) \(\frac{{27}}{{15}}{x^3}y{z^5}:\frac{9}{5}x{z^2}\).
Phân tích các đa thức sau thành nhân tử:
a) \(3{x^2}y - 9x{y^2} + 12{x^2}{y^2}\);
b) \({x^3} - 6{x^2}y + 12x{y^2} - 8{y^3}\);
c) \[3{x^3} + xy - 12x{y^2} - 2{y^2}\].
Cho biểu thức: \(P = \frac{2}{{{x^2} - x}} + \frac{2}{{{x^2} + x + 1}} + \frac{{4x}}{{1 - {x^3}}}\) với \(x \ne 0;\,\,x \ne 1.\)
a) Rút gọn biểu thức \(P\);
b) Tính giá trị biểu thức \(P\) tại \(x = 2\).
Một chiếc đèn thả trần có dạng hình chóp tam giác đều có tất cả các cạnh đều khoảng \[20\,\,{\rm{cm}}.\] Độ dài trung đoạn khoảng \[17,32{\rm{ cm}}.\] Tính diện tích xung quanh của chiếc đèn thả trần đó.
Cho hình chóp tam giác đều \[S.ABC\] có cạnh đáy bằng \[4\,\,cm\] và chiều cao tam giác đáy là \[3,5\,\,{\rm{cm;}}\] trung đoạn bằng \[5\,\,{\rm{cm}}.\] Tính diện tích xung quanh và diện tích toàn phần (tức là tổng diện tích các mặt) của hình chóp.

Cho biểu thức \(A = 12x - 8y - 4{x^2} - {y^2} + 1\). Tính giá trị lớn nhất của biểu thức \(A.\)








