Bộ 5 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 3
21 câu hỏi
Cho các biểu thức đại số sau:
\( - 6{x^2}y;\,\,\,{x^3} - \frac{1}{2}xy;\,\,\,5{z^3};\,\,\, - \frac{4}{7}y{z^2}.5;\,\,\,\, - 3x + 7y;\,\,\,\,\left( {\sqrt 2 - 1} \right)x;\,\,\,\,x\sqrt y \).
Có bao nhiêu đơn thức trong các biểu thức đã cho ở trên?
5.
4.
3.
2.
Bậc của đơn thức \(2{x^2}y{\left( {2{y^3}} \right)^2}\) là
5.
7.
8.
9.
Khẳng định nào sau đây là đúng?
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
\({\left( {A + B} \right)^2} = {A^2} + AB + {B^2}\).
\({\left( {A + B} \right)^2} = {A^2} + {B^2}\).
\({\left( {A + B} \right)^2} = {A^2} - 2AB + {B^2}\).
Phân thức nào sau đây có tử thức là \(2x - 1\) và mẫu thức là \({x^2} - 1?\)
\(\frac{{{x^2} - 1}}{{2x - 1}}.\)
\(\frac{{2x - 1}}{{{x^2} + 1}}.\)
\(\frac{{2x - 1}}{{{x^2} - 1}}.\)
\(\frac{{{x^2} - 1}}{{2x + 1}}.\)
Tổng số cạnh bên và cạnh đáy của một hình chóp tam giác đều là
4.
6.
8.
10.
Diện tích xung quanh của hình chóp đều bằng
Tích nửa chu vi đáy và đường cao của hình chóp.
Tổng chu vi đáy và trung đoạn.
Tích chu vi đáy và trung đoạn.
Tích nửa chu vi đáy và trung đoạn.
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau?
\(15\;\;{\rm{cm}};\,\,8\;\;{\rm{cm;}}\,\,{\rm{18}}\;\;{\rm{cm}}\,{\rm{.}}\)
\(2\;\;{\rm{cm}};\,\,3\;\;{\rm{cm;}}\,\,4\;\;{\rm{cm}}\,{\rm{.}}\)
\(5\;\;{\rm{m}};\,\,6\;\;{\rm{m;}}\,\,{\rm{8}}\;\;{\rm{m}}\,{\rm{.}}\)
\[21\;\;{\rm{dm}};\,\,20\;\;{\rm{dm;}}\,\,29\;\;{\rm{dm}}\,{\rm{.}}\]
Phát biểu nào sau đây là sai?
Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là hình vuông.
Tứ giác có hai đường chéo bằng nhau là hình bình hành.
Tứ giác có 4 cạnh bằng nhau là hình thoi.
Tứ giác có 4 góc bằng nhau là hình chữ nhật.
Dữ liệu về số người trong mỗi nhà của các nhà gần nhà em thuộc loại dữ liệu nào trong các loại dữ liệu sau?
Dữ liệu số rời rạc.
Dữ liệu không là số có thể sắp thứ tự.
Dữ liệu số liên tục.
Dữ liệu không là số không thể sắp thứ tự.
Nhiệt độ trung bình các tháng trong năm của một quốc gia được biểu diễn trong bảng sau:
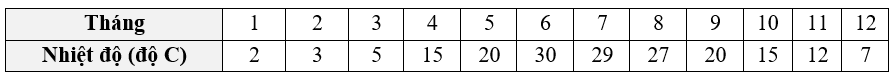
Biểu đồ thích hợp để biểu diễn dữ liệu trong bảng trên là
Biểu đồ hình quạt tròn.
Biểu đồ cột tranh.
Biểu đồ đoạn thẳng.
Không thể biểu diễn được.
Mỗi câu lạc bộ tại trường Trung học cơ sở Kim Đồng có 15 học sinh. Số lượng học sinh nam và học sinh nữ của mỗi câu lạc bộ được biểu diễn trong bảng số liệu sau đây.
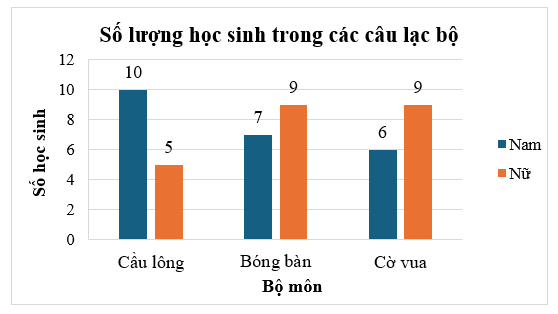
Biết trong biểu đồ trên có dữ liệu thống kê của câu lạc bộ chưa chính xác, đó là
Cầu lông.
Bóng bán.
Cờ vua.
Cầu lông, cờ vua.
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 bằng bảng dưới đây.

(Nguồn: Niên giám thống kê 2021)
Hỏi số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa năm 2020 giảm bao nhiêu phần trăm so với năm 2019? (Kết quả làm tròn đến hàng phần mười)
\(35,6\% \).
\(52,5\% \).
\(32,5\% \).
\(61,9\% \).
Cho đa thức \(G = \left( {7{x^5}{y^4}{z^3} - 3{x^4}y{z^2} + 2{x^2}{y^2}z} \right):{x^2}yz\).
Đa thức \[A\] thỏa mãn \(A + 14{x^3}{y^3}{z^2} - 6{x^2}z = G\).
a) Bậc của đa thức \(G\) là 8.
b) Giá trị của biểu thức \(G\) tại \(x = 1\,;\,\,y = - 1\,;\,\,z = 1\) là 12.
c) Đa thức \[A\] có hạng tử tự do là 2.
d) Tổng của hai đa thức \[A\] và \(G\) là một đơn thức.
Cho hình bình hành \(ABCD\) có \(BC = 2AB\), \(\widehat A = 60^\circ \). Gọi \(E\), \(F\) theo thứ tự là trung điểm của \(BC\), \(AD\). Trên tia \(AB\) lấy điểm \(I\) sao cho \(B\) là trung điểm của \(AI.\)
a) \(AB = \frac{2}{3}BE\).
b) Tứ giác \(ABEF\) là hình chữ nhật.
c) Tam giác \(ADI\) cân tại \(D\).
d) \(\widehat {AED} = 90^\circ \).
Cho biểu thức \(M = {\left( {x + 3} \right)^3} - \left( {x + 9} \right)\left( {{x^2} + 27} \right)\). Giá trị của biểu thức \(M\) bằng bao nhiêu?
Cho biểu thức \[S = \left( {\frac{x}{{x + 3}} - \frac{2}{{x - 3}} + \frac{{{x^2} - 1}}{{9 - {x^2}}}} \right):\left( {2 - \frac{{x + 5}}{{3 + x}}} \right)\,\,\,\left( {x \ne - 3\,;\,\,x \ne 3\,;\,\,x \ne - 1} \right)\].
Hỏi sau khi rút gọn biểu thức \[S\] ta được phân thức có tử thức bằng bao nhiêu?
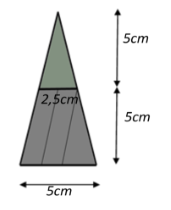
Hình ảnh bên là ảnh của một lọ nước hoa hình kim tự tháp. Khi đậy nắp, lọ có dạng hình chóp tứ giác đều (tính cả thân lọ và nắp lọ) trong đó nắp lọ cũng là hình chóp tứ giác đều có chiều cao \[5{\rm{ cm}},\] cạnh đáy \[2,5{\rm{ cm}}.\] Chiều cao thân lọ và cạnh đáy lọ đều bằng chiều cao của nắp lọ. Bỏ qua độ dày của vỏ. Tính dung tích của lọ nước hoa đó ra đơn vị mi – li – lít (làm tròn kết quả đến hàng đơn vị).
Cho tứ giác \(MNPQ\) có \(PM\) là tia phân giác của góc \(\widehat {NPQ}.\) Biết \(\widehat {QMN} = 110^\circ ,\) \(\widehat {N\,} = 120^\circ \) và \(\widehat {Q\,} = 60^\circ .\) Tính số đo của \(\widehat {MPQ}\) (đơn vị: độ).
(1,5 điểm) Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của Việt Nam qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng).
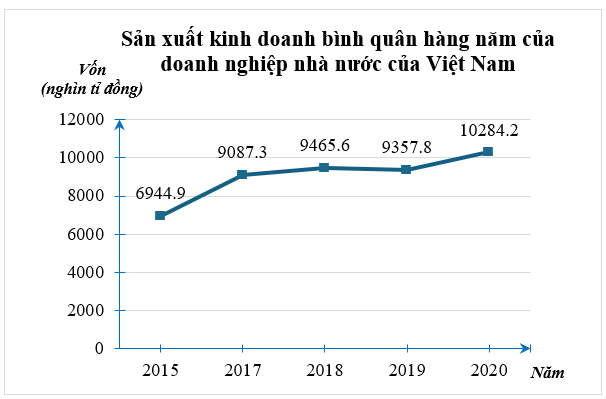
(Nguồn: Niên giám thống kê 2021)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
c) Tính tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại (làm tròn kết quả đến hàng phần mười).
(1,0 điểm) Cho hình vuông \[ABCD.\] Lấy điểm \[M\] thuộc đường chéo \[BD.\] Kẻ \[ME\] vuông góc với \(AB\) tại \[E,{\rm{ }}MF\] vuông góc với \[AD\] tại \[F.\]
a) Tứ giác \(AEMF\) là hình gì? Vì sao?
b) Xác định vị trí của điểm \[M\] trên đường chéo \[BD\] để diện tích của tứ giác \[AEMF\] lớn nhất.
(0,5 điểm) Cho \(a + b + c = 0\,;\,\,x + y + z = 0\) và \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0.\)
Chứng minh rằng: \(a{x^2} + b{y^2} + c{z^2} = 0.\)








