Bộ 2 Đề kiểm tra cuối học kì 2 Toán 10 Cánh Diều - Đề 02 có đáp án
40 câu hỏi
Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.
31;
16;
47;
15.
Số cách sắp xếp 6 bạn học sinh thành một hàng dọc là:
6 cách;
12 cách;
720 cách;
18 cách.
Có bao nhiêu số tự nhiên có 5 chữ số, các chữ số khác 0 và đôi một khác nhau.
5!;
95;
\(A_9^5\);
59.
Khai triển biểu thức (a + 2b)5 ta thu được kết quả là:
a5 + 10a4b + 40a3b2 + 80a2b3 + 80ab4 + 32b5;
a5 – 10a4b – 40a3b2 – 80a2b3 – 80ab4 – 32b5;
a5 + 20a4b + 30a3b2 + 80a2b3 + 80ab4 + 32b5;
a5 + 10a4b + 40a3b2 + 60a2b3 + 60ab4 + 32b5.
Tổng các hệ số trong khai triển \(P\left( x \right) = {\left( {1 + x} \right)^5}\) là:
30;
31;
32;
33.
Giá trị nào dưới đây là giá trị chính xác của số π ?
3,14;
3,1;
3,146;
Không có câu trả lời đúng.
Quy tròn số 3,1234567 đến hàng phần nghìn. Số gần đúng nhận được là:
3,124;
3,123;
3,12;
3,1235.
Thực hiện đo chiều dài của bốn cây cầu, kết quả đo đạc nào trong các kết quả sau đây là chính xác nhất?
15,34 m ± 0,01 m;
127,4 m ± 0,2 m;
2135,8 m ± 0,5 m;
63,47 m ± 0,15 m.
Giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
trung bình;
tứ phân vị;
trung vị;
mốt.
Cho mẫu số liệu sau: 11; 16; 17; 19; 20; 21; 22; 23; 23; 24; 25. Trung vị của mẫu số liệu là
21;
20,5;
21,5;
22.
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
Năng suất lúa (tạ/ha) | 25 | 30 | 35 | 40 | 45 |
Tần số | 4 | 7 | 9 | 6 | 5 |
So sánh Q3 và Q1 ?
Q3 > Q1;
Q3 < Q1;
Q1 = Q3;
Q3 = 3Q1.
Điểm thi học kì I môn Toán của lớp 10A được thống kê trong bảng sau:
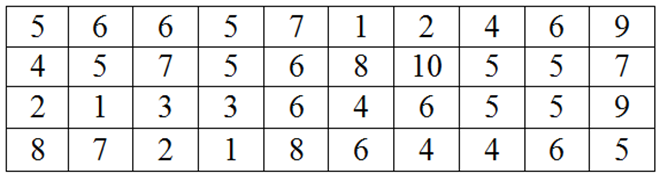
Điểm trung bình môn Toán của lớp 10A2 là
4;
5,5;
5,45;
6.
Chọn khẳng định đúng: “Trong một mẫu số liệu, khoảng biến thiên là…”
hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;
tổng số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;
tích giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;
thương giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.
Sản lượng lúa (đơn vị là tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Phương sai của bảng số liệu trên là:
1,52;
1,53;
1,54;
1,55.
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
Năng suất lúa (tạ/ha) | 25 | 30 | 35 | 40 | 45 |
Tần số | 4 | 7 | 9 | 6 | 5 |
Khoảng tứ phân vị của bảng số liệu trên là:
30;
10;
20;
5.
Gieo một đồng xu ba lần liên tiếp. Xác suất để ba lần tung kết quả giống nhau là:
0,25;
0,5;
1;
0,75.
Một túi chứa 2 viên bi màu trắng và 3 viên bi màu đen. Lấy ngẫu nhiên 3 viên bi. Xác suất để lấy được ít nhất 1 bi trắng là:
0,9;
0,8;
0,1;
0,2.
Xác suất của biến cố A, kí hiệu là:
P(A);
n(A);
C(A);
Ω(A).
Trong mặt phẳng tọa độ Oxy, cho G(3; 5). Tọa độ của \(\overrightarrow {OG} \) là
(3; –5);
(5; 3);
(–3; –5);
(3; 5).
Trong mặt phẳng tọa độ Oxy, cho hai điểm \(M\left( {{x_M};{y_M}} \right)\) và \(N\left( {{x_N};{y_N}} \right)\). Khi đó ta có tọa độ \(\overrightarrow {MN} \) là:
\(\overrightarrow {MN} = \left( {{x_N} + {x_M};{y_N} + {y_M}} \right)\);
\(\overrightarrow {MN} = \left( {{x_M} - {x_N};{y_N} - {y_M}} \right)\);
\(\overrightarrow {MN} = \left( {{x_M} - {x_N};{y_M} - {y_N}} \right)\);
\(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M}} \right)\).
Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–1; 3) và C(5; 2). Tọa độ của \(\overrightarrow {BC} \) là:
\(\overrightarrow {BC} = \left( {6; - 1} \right)\);
\(\overrightarrow {BC} = \left( { - 6;1} \right)\);
\(\overrightarrow {BC} = \left( {4;5} \right)\);
\(\overrightarrow {BC} = \left( { - 6; - 1} \right)\).
Trong mặt phẳng tọa độ Oxy, cho \(\vec a = \left( {{a_1};{a_2}} \right),\,\,\vec b = \left( {{b_1};{b_2}} \right)\) và \(\vec x = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right)\). Khi đó \(\vec x\) bằng:
\(\vec a.\vec b\);
\(\vec a + \vec b\);
\(\vec a - \vec b\);
\(k\vec a\,\,\,\left( {k \in \mathbb{R}} \right)\).
Trong mặt phẳng tọa độ Oxy, cho \(\vec u = \left( {3; - 6} \right)\). Khi đó \(\frac{1}{2}\vec u\) là:
\(\frac{1}{2}\vec u = \left( {6; - 12} \right)\);
\(\frac{1}{2}\vec u = \left( {\frac{5}{2}; - \frac{{13}}{2}} \right)\);
\(\frac{1}{2}\vec u = \left( {\frac{7}{2}; - \frac{{11}}{2}} \right)\);
\(\frac{1}{2}\vec u = \left( {\frac{3}{2}; - 3} \right)\).
Cho đường thẳng d có phương trình: \(\left\{ \begin{array}{l}x = 2 + 3t\\y = - 3 - t\end{array} \right.\). Một vectơ chỉ phương của d có tọa độ là:
(2; –3);
(3; –1);
(3; 1);
(3; –3).
Cho đường thẳng ∆: x – 3y – 2 = 0. Tọa độ của vectơ nào sau đây không phải là vectơ pháp tuyến của ∆?
\({\vec n_1} = \left( {1; - 3} \right)\);
\({\vec n_2} = \left( { - 2;6} \right)\);
\({\vec n_3} = \left( {\frac{1}{3}; - 1} \right)\);
\({\vec n_4} = \left( {3;1} \right)\).
Cho tam giác ABC có tọa độ 3 đỉnh A(4; 5), B(–6; –1), C(1; 1). Phương trình đường cao BH của tam giác ABC là:
3x – 4y – 14 = 0;
3x + 4y – 22 = 0;
3x + 4y + 22 = 0;
3x – 4y + 14 = 0.
Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Khi đó phương trình đường trung trực của cạnh AB có phương trình là:
13x – 3y + 100 = 0;
3x – 13y – 140 = 0;
3x – 13y + 140 = 0;
13x + 3y – 100 = 0.
Cho đường thẳng d1, d2 có vectơ pháp tuyến lần lượt là \[{\vec n_1} = \left( {a;b} \right),\,\,{\vec n_2} = \left( {c;d} \right)\]. Kết luận nào sau đây đúng?
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {ab + cd} \right|}}{{\sqrt {{a^2} + {c^2}} .\sqrt {{b^2} + {d^2}} }}\);
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {ac + bd} \right|}}{{\sqrt {{a^2} + {c^2}} .\sqrt {{b^2} + {d^2}} }}\);
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {ac + bd} \right|}}{{\sqrt {{a^2} + {b^2}} .\sqrt {{c^2} + {d^2}} }}\);
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{ac + bd}}{{\sqrt {{a^2} + {b^2}} .\sqrt {{c^2} + {d^2}} }}\).
Vị trí tương đối của hai đường thẳng \({d_1}:\frac{x}{2} - \frac{y}{3} = 1\) và d2: 6x – 4y – 8 = 0 là:
Song song;
Trùng nhau;
Cắt nhau nhưng không vuông góc với nhau;
Vuông góc với nhau.
Tâm của đường tròn (C) có phương trình: (x – 2)2 + (y + 5)2 = 12 là:
D(2; 5);
E(5; 2);
F(2; –5);
G(–2; 5).
Đường tròn tâm I(1; 4) và đi qua điểm B(2; 6) có phương trình là:
(x + 1)2 + (y + 4)2 = 5;
\({\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} = \sqrt 5 \);
\({\left( {x + 1} \right)^2} + {\left( {y + 4} \right)^2} = \sqrt 5 \);
(x – 1)2 + (y – 4)2 = 5.
Cho đường tròn (C): (x – 2)2 + (y – 2)2 = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:
x + y – 4 = 0 hoặc x – y – 2 = 0;
x = 5 hoặc y = –1;
2x – y – 3 = 0 hoặc 3x + 2y – 2 = 0;
3x – 2y – 2 = 0 hoặc 2x + 3y + 5 = 0.
Cho hai điểm F1, F2 cố định có khoảng cách F1F2 = 2c (c > 0) và một số a < c và a > 0. Tập hợp các điểm M sao cho |MF1 – MF2| = 2a được gọi là:
Đường hypebol;
Đường elip;
Đường parabol;
Đường tròn.
Điểm nào là tiêu điểm của parabol y2 = 5x?
F(5; 0);
\(F\left( {\frac{5}{2};0} \right)\);
\(F\left( { \pm \frac{5}{4};0} \right)\);
\(F\left( {\frac{5}{4};0} \right)\).
Cho elip (E): 9x2 + 36y2 – 144 = 0. Tỉ số \(\frac{c}{a}\) bằng:
\(\frac{{\sqrt 3 }}{2}\);
\(\frac{{2\sqrt 3 }}{3}\);
\(\sqrt 3 \);
\(\frac{{\sqrt 3 }}{3}\).
Một bàn dài có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 4 ghế. Người ta xếp chỗ ngồi cho 4 học sinh trường A và 4 học sinh trường B vào bàn nói trên. Hỏi xác suất xếp các học sinh vào hai dãy ghế sao cho bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau?
Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm (cho giống lúa mới) có cùng diện tích được trình bày trong bảng phân bố tần số sau đây:
Sản lượng | 20 | 21 | 22 | 23 | 24 |
Tần số | 5 | 8 | 11 | 10 | 6 |
Hỏi sản lượng lúa trung bình thu được là bao nhiêu tạ? Tìm khoảng tứ phân vị của dãy số liệu trên.
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Viết phương trình đường thẳng (∆) song song với (d): 4x – 3y + 3 = 0 và tiếp xúc với (C).
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Viết phương trình đường thẳng (d) qua A(3; 2) và tiếp xúc với (C).
Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 – 2x + 2y – 2 = 0.
Tìm điểm M thuộc (d’): x – 2y – 1 = 0 sao cho từ M vẽ được hai tiếp tuyến đến (C) vuông góc với nhau.








