Bộ 15 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 (Đề 3)
39 câu hỏi
Tìm khẳng định sai
.
.
.
Tìm ?
.
.
.
.
Tìm họ nguyên hàm của hàm số .
.
.
.
Nếu thì f(x) bằng
.
.
.
.
Tìm nguyên hàm của hàm số
.
.
.
.
Tính
.
.
.
.
Biết F(x) là nguyên hàm của hàm số và . Tìm F(x).
.
.
.
.
Cho F(x) là một nguyên hàm của hàm số thỏa mãn . Tìm tập nghiệm S của phương trình
.
.
.
Giá trị của tích phân bằng
9.
8.
7.
6.
Giá trị của tích phân bằng
.
.
.
1.
Giả sử . Giá trị đúng của c là
1.
3.
8.
9.
Một chiếc ôtô chuyển động với vận tốc . Quãng đường ôtô đó đi được trong giây đầu tiên là (kết quả làm tròn đến hàng trăm)
8,23m.
8,31m.
8,24m.
8, 32m.
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số liên tục, trục hoành và hai đường thẳng được tính theo công thức:
.
.
.
.
Hình phẳng (H) giới hạn bởi các đường , và hai đường x = 0, x = 2. Công thức nào sau đây tính diện tích hình phẳng (H)?
.
.
.
.
Cho hình phẳng giới hạn bởi các đường quay xung quanh trục Ox tạo thành khối tròn xoay có thể tích bằng . Tìm a và b
.
.
.
Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây: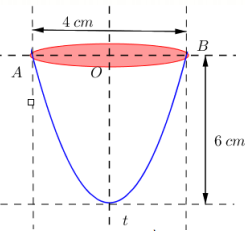
Người ta đo được đường kính của miệng ly là 4cm và chiều cao là 6cm. Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một Parabol. Tính thể tích của vật thể đã cho
.
.
.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm và . Tìm tọa độ trung điểm I của đoạn thẳng AB.
.
.
.
.
Tích vô hướng của hai vectơ trong không gian bằng:
10.
12.
13.
14.
Trong không gian với hệ toạ độ Oxyz cho các véctơ , , . Gọi . Tìm toạ độ .
.
.
.
.
Trong không gian Oxyz cho tam giác ABC với và tọa độ trọng tâm của tam giác là . Tọa độ đỉnh C là
.
.
.
.
Trong không gian Oxyz, cho hai điểm . Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là
.
.
.
.
Trong không gian Oxyz cho hai véctơ , . Tích có hướng của hai véctơ và là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ . Giá trị của m để là
-1.
0.
1.
2.
Trong không gian với hệ toạ độ Oxyz, cho ba điểm và . Diện tích tam giác ABC là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có , , và . Tính thể tích V của tứ diện ABCD.
.
.
.
.
Cho có 3 đỉnh Để thì:
.
.
.
.
Trong không gian với hệ tọa độ Oxyz cho mặt cầu có phương trình: Mặt cầu có tâm I và bán kính R là:
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, mặt cầu có đường kính AB với và có phương trình là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz cho . Mặt cầu (S) tâm I và đi qua điểm A có phương trình là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, mặt cầu (S) có tâm và có thể tích . Khi đó phương trình của mặt cầu (S) là:
Trong không gian với hệ tọa độ Oxyz, mặt cầu đi qua bốn điểm , , và có phương trình là:
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng . Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P)?
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm và có véc tơ pháp tuyến có phương trình là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, cho điểm và mp . Phương trình mặt phẳng (Q) đi qua A song song với mặt phẳng (P) là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, đường thẳng có một véctơ chỉ phương là
.
.
.
.
Trong không gian với hệ tọa độ Oxyz, phương trình tham số của đường thẳng đi qua điểm và có vectơ chỉ phương là
Trong không gian với hệ tọa độ Oxyz, cho , phương trình đường thẳng d đi qua hai điểm A, B là:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng : và điểm . Phương trình tham số đường thẳng d đi qua điểm A đồng thời vuông góc và cắt đường thẳng là:
.
.
.
.
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng và . Phương trình đường vuông góc chung của hai đường thẳng là
.
.
.
.