Bộ 15 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 (Đề 11)

Tính nguyên hàm $I=\int \frac{dx}{2-3x}.$

Nguyên hàm của hàm số $f\left(x\right)\text{=}{x}^2–3x+ \frac{1}{x}$ là:

Nguyên hàm của hàm số $f\left(x\right)=\sqrt[3]{x}$ là:

Tìm nguyên hàm F(x) của hàm số $f\left(x\right)=4x^3-3x^2+2$ biết $F(-1)=3.$

Tìm nguyên hàm: $\int {(1+\sin x)}^{2}dx$

Cho $f\left(x\right)=\frac{4m}{\pi }+{\sin }^{2}x$. Tìm m để nguyên hàm F(x) của f(x) thỏa mãn F(0) = 1 và $F\left(\frac{\pi }{4}\right)=\frac{\pi }{8}$

Cho hàm số $y=f\left(x\right)$ liên tục, không âm trên R thỏa mãn $f\left(x\right).f^{\text{'}}\left(x\right)=2x\sqrt{{\left(f\left(x\right)\right)}^2+1}$ và $f\left(0\right)=0$. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y=f\left(x\right)$ trên đoạn $\left[1;3\right]$ lần lượt là:

Cho f(x) là hàm số chẵn và liên tục trên R thỏa mãn $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=2$. Khi đó giá trị tích phân $\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ là:

Cho hai tích phân $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\sin }^{2}xdx$ và $J=\underset{0}{\overset{\frac{\pi }{2}}{\int }}{\cos }^{2}xdx$. Hãy chỉ ra khẳng định đúng:

Tính $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}(2x+1)\sin 2xdx$.
Lời giải sau sai từ bước nào:
Bước 1: Đặt u = 2x + 1; dv = sin2xdx
Bước 2: Ta có du = 2 dx; v = cos2x
Bước 3: $I=(2x+1)cos2x{|}_0^{\frac{\pi }{2}}-\underset{0}{\overset{\frac{\pi }{2}}{\int }}2\cos 2xdx=(2x+1)\cos 2x{|}_0^{\frac{\pi }{2}}-2\sin 2x{|}_0^{\frac{\pi }{2}}$
Bước 4: Vậy $I=-\pi -2$

Nếu $f\left(1\right)=12,f\text{'}\left(x\right)$ liên tục và $\underset{1}{\overset{4}{\int }}f\text{'}\left(x\right)dx=17$, giá trị của f(4) bằng:

Cho đồ thị hàm số f(x). Diện tích hình phẳng (phần gạch chéo trong Hình 1) là: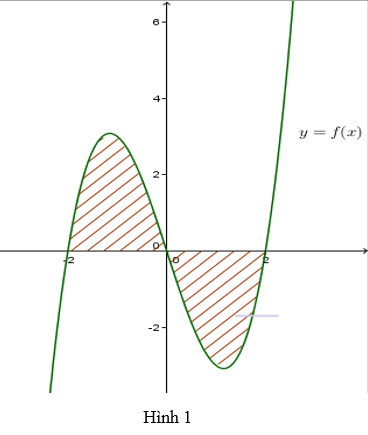

Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành được tính theo công thức nào?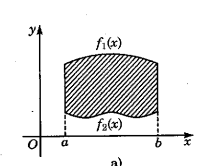

Diện tích hình phẳng giới hạn bởi các đường $y=4x-x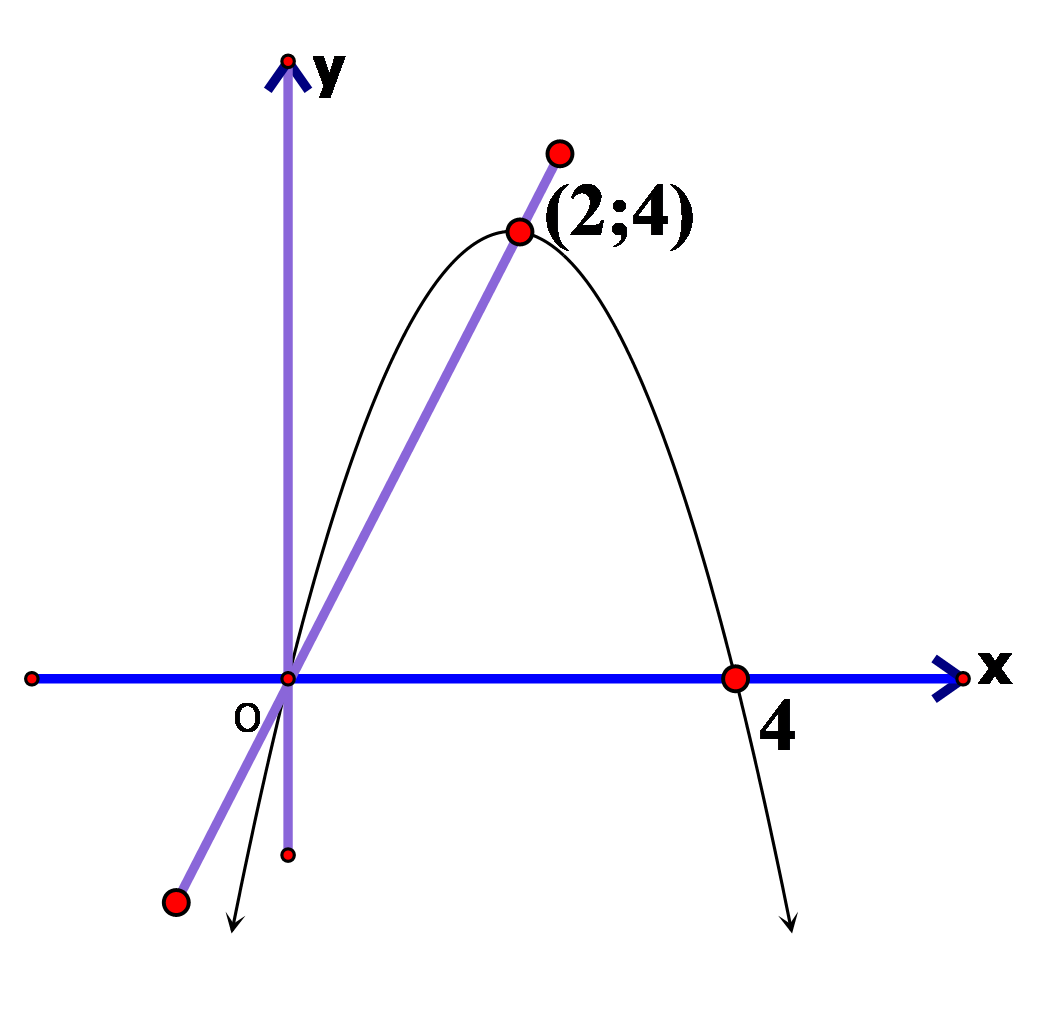^2$ và $y=2x$ là:

Cho hai hàm số y = f(x), y = g(x) có đồ thị (C₁) và (C₂) liên tục trên [a;b] thì công thức tính diện tích hình phẳng giới hạn bởi (C1), (C₂) và hai đường thẳng x = a, x = b là:

Cho hình phẳng (H) giới hạn bởi đường thẳng y = x; trục hoành và đường thẳng x = m, m > 0. Thể tích khối tròn xoay tạo bởi khi quay (H) quanh trục hoành là $9\pi$ (đvtt). Giá trị của tham số m là:

Trong không gian với hệ trục tọa độ Oxyz, điểm nào sau đây thuộc trục Oz

Trong không gian với hệ trục tọa độ Oxyz cho véctơ $\overrightarrow{a}\left(1;2;3\right).$ Hỏi véctơ nào dưới đây cùng phương với $\overrightarrow{a}?$

Trong không gian với hệ tọa độ Oxyz cho hai điểm A(2;0;0), B(0;-3;0), C(0;0;4). Tìm điểm D sao cho tứ giác ABCD là hình bình hành.

Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A(-2;1;0) và B với $B\in \text{Ox,}B\in \text{Oy,}B\in \text{Oz.}$ Tính độ dài của AB.

Trong không gian Oxyz cho ba vectơ $\overrightarrow{a},\overrightarrow{b}$ và $\overrightarrow{c}$ khác $\overrightarrow{0}$. Khẳng định nào sau đây sai?

Trong không gian với hệ trục tọa độ Oxyz cho tứ diện ABCD với $A(0,0,1),B(2,3,5),C(6,2,3),D(3,7,2).$ Thể tích của tứ diện ABCD bằng

Trong không gian với hệ trục tọa độ Oxyz cho các điểm $A(3;-4;0),B(0;2;4),C(4;2;1).$ Tìm tọa độ điểm D trên trục Ox sao cho AD=BC.

Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2;-1;3), B(4;0;1) và C(-10;5;3). Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)

Trong không gian với hệ tọa độ Oxyz cho $\overrightarrow{a}=(2;4;-4),\overrightarrow{b}=(2;1;-2).$ Hãy chọn đáp án đúng nhất.

Trong không gian với hệ trục tọa độ Oxyz cho lăng trụ tam giác ABC.A’B’C’ có $A(1;1;1;),B(1;2;1);C(1;1;2),A\text{'}(2;2;1).$ Phương trình mặt cầu đi qua bốn điểm A, B, C, A’ là

Viết phương trình mặt cầu tâm I(1;-2;3) và tiếp xúc với trục Oy

Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;-6;4). Phương trình nào sau đây là phương trình mặt cầu đường kính OA?

Trong không gian với hệ trục tọa độ Oxyz xác định tọa độ tâm I và bán kính r của mặt cầu $\left(S\right):x^2+y^2+z^2-2x+6y-8z+1=0.$

Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng $\left(d\right):\left\{\begin{array}{c}x=2-t\\ y=1+2t\\ z=-3\end{array}\right.,t\in R$ và điểm $A(-2;0;1).$ Phương trình mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng (d) là

Trong không gian với hệ trục tọa độ Oxyz phương trình mặt phẳng đi qua điểm A(1;-2;0) và có vectơ pháp tuyến $\overrightarrow{n}=(2;-1;3)$ là phương trình nào sau đây?

Trong không gian với hệ toạ độ Oxyz phương trình mặt phẳng trung trực của đoạn thẳng AB với $A\left(1;-2;4\right),B\left(3;6;2\right)$ là phương trình nào sau đây?

Trong không gian với hệ trục tọa độ Oxyz phương trình mặt phẳng đi qua ba điểm $I(3;-1;5),M(4;2;-1),N(1;-2;3)$ là phương trình nào sau đây?

Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): 2x - 3y + 7z - 9 = 0. Véctơ pháp tuyến của (P) là

Trong không gian với hệ tọa độ Oxyz cho đường thẳng $d:\left\{\begin{array}{l}x=0\\ y=t\\ z=2-t\end{array}\right.$. Vectơ nào dưới đây là vectơ chỉ phương của đường thẳng d?

Cho hai đường thẳng $d_1:\left\{\begin{array}{l}x=2+t\\ y=-1+t\\ z=3\end{array}\right.$ và $d_2:\left\{\begin{array}{l}x=1-t\\ y=2\\ z=-2+t\end{array}\right.$. Tính góc giữa hai đường thẳng d₁ và d₂

Trong không gian với hệ toạ độ Oxyz gọi $\Delta$là đường thẳng đi qua điểm $M\left(2;0;-3\right)$ và vuông góc với mặt phẳng $\left(\alpha \right):2x-3y+5z+4=0$. Phương trình chính tắc của $\Delta$ là phương trình nào?

Trong không gian Oxyz cho ba điểm A(1;-1;3), B(4;3;-1), C(3;-3;2). Viết phương trình đường thẳng đi qua A và song song BC