Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 5)
21 câu hỏi
Hàm số nào sau đây không là hàm số bậc nhất?
\(y = \frac{x}{2} - \frac{3}{2}.\)
\(y = 3x.\)
\(y = \frac{2}{3}{x^2} + x - 1.\)
\(y = \frac{{7x}}{4} - \frac{2}{3}.\)
Đồ thị hàm số \(y = ax{\rm{ }}\left( {a \ne 0} \right)\) là một đường thẳng luôn đi qua
gốc tọa độ \(O\left( {0;0} \right).\)
điểm \(A\left( {1;0} \right).\)
điểm \(B\left( {0;1} \right).\)
điểm \(O\left( {0; - 1} \right).\)
Đường thẳng \(y = - 3x - 2022\) tạo với trục \(Ox\) một góc như thế nào?
góc tù.
góc bẹt.
góc vuông.
góc nhọn.
Trong các phát biểu sau, phát biểu nào sai?
Đồ thị hàm số \(y = ax + b\left( {a \ne 0;b \ne 0} \right)\) là đường thẳng cắt đường thẳng \(y = ax.\)
Đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\) là đường thẳng song song với đường thẳng \(y = ax\) nếu \(b \ne 0\) và trùng với đường thẳng \(y = ax\) nếu \(b = 0.\)
Đồ thị hàm số \(y = ax + b\left( {a \ne 0;b \ne 0} \right)\) là đường thẳng cắt trục tung tại điểm có tung độ bằng \(b = 0.\)
Đồ thị hàm số \(y = ax + b\left( {a \ne 0;b \ne 0} \right)\) là đường thẳng không đi qua gốc tọa độ.
Đưa phương trình \(5x - \left( {6 - x} \right) = 12\) về dạng \(ax + b = 0\) ta được
\(4x + 6 = 0.\)
\(4x - 18 = 0\).
\(5x - 6 = 0\).
\(6x - 18 = 0\).
Giá trị \(x = - 4\) là nghiệm của phương trình nào dưới đây?
\( - \frac{5}{2}x + 1 = 11\).
\( - \frac{5}{2}x = - 10\).
\(3x - 8 = 0\).
\(3x - 1 = x + 7\).
Năm nay Trang \(x\) (tuổi), sau \(6\) năm nữa tuổi của Trang là
\(6x.\)
\(x + 6.\)
\(6 - x\).
\(x\left( {x + 6} \right).\)
Tỉ lệ học sinh bị cận ở một trường trung học cơ sở là \(0,2\). Nếu trường đó có \(x\) (học sinh) thì số học sinh không bị cận thị ở trường đó là
\(0,2x\).
\(\frac{x}{{0,2}}\).
\(0,8x.\)
\(\frac{x}{{0,8}}.\)
Cho tam giác \(MNP\) có \(H \in MN;K \in MP\). Điều kiện không kết luận được \(HK\parallel NP\) là
\(\frac{{MH}}{{MN}} = \frac{{MK}}{{MP}}.\)
\(\frac{{MH}}{{HN}} = \frac{{MK}}{{KP}}.\)
\(\frac{{HN}}{{MN}} = \frac{{MP}}{{KP}}.\)
\(\frac{{NH}}{{MN}} = \frac{{PK}}{{MP}}.\)
Cho hình vẽ bên, biết \(MN\parallel BC,NP\parallel AB\).
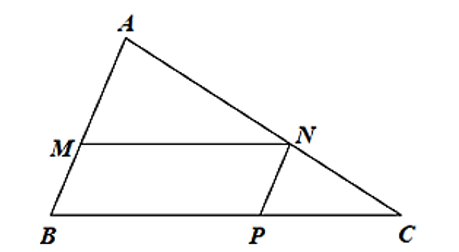
Khẳng định nào sau đây là sai?
\(\frac{{MA}}{{MN}} = \frac{{AB}}{{BC}}.\)
\(\frac{{AN}}{{AC}} = \frac{{BP}}{{BC}}.\)
\(\frac{{CP}}{{BP}} = \frac{{CN}}{{AN}}.\)
\(\frac{{MN}}{{BC}} = \frac{{NP}}{{AB}}.\)
Cho \(\Delta ABC\) có \(BM\) là tia phân giác của \(\widehat {ABC}\)\(\left( {M \in AC} \right)\).
Khẳng định nào sau đây là sai?
\(\frac{{AB}}{{AM}} = \frac{{BC}}{{MC}}.\)
\(\frac{{AB}}{{BC}} = \frac{{AM}}{{CM}}.\)
\(\frac{{BC}}{{AB}} = \frac{{AC}}{{AM}}.\)
\(AM = \frac{{AB.AC}}{{AB + BC}}.\)
Cho hình vẽ bên. Biết \(DE = 13{\rm{ cm}}\), độ dài đoạn thẳng \(HE\) là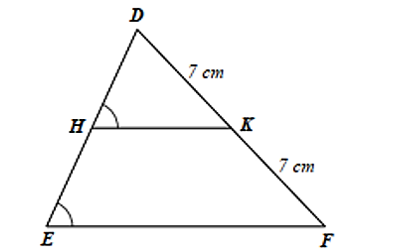
\(5,5{\rm{ cm}}{\rm{.}}\)
\(6,5{\rm{ cm}}{\rm{.}}\)
\({\rm{7 cm}}{\rm{.}}\)
\({\rm{8 cm}}{\rm{.}}\)
Một miếng đất hình chữ nhật có chiều dài hơn chiều rộng \(25{\rm{ m}}\). Nếu giảm chiều dài đi \(25{\rm{ m}}\) thì diện tích sẽ nhỏ hơn diện tích ban đầu là \(1{\rm{ }}000{\rm{ }}{{\rm{m}}^2}\). Gọi chiều dài ban đầu của miếng dất là \(x\) \(\left( {x > 25,{\rm{ m}}} \right).\)
a) Chiều rộng ban đầu của miếng đất là \(x - 25{\rm{ }}\left( {\rm{m}} \right)\).
b) Khi chiều dài giảm đi \(25{\rm{ m}}\)ta được chiều dài mới bằng chiều rộng ban đầu của mảnh đất.
c) Phương trình mô tả bài toán là \(x\left( {x - 25} \right) - \left( {x - 25} \right)\left( {x - 25} \right) = 1{\rm{ }}000\).
d) Diện tích ban đầu của mảnh đất là \({\rm{2 600 }}\left( {{{\rm{m}}^2}} \right)\).
Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD\). Gọi \(M\) là trung điểm của \(CD\), \(E\) là giao điểm của \(MA\) và \(BD\), \(F\) là giao điểm của \(MB\) và \(AC\). Đường thẳng \(EF\) cắt \(AD,BC\) lần lượt tại \(H\) và \(N\). Biết \(AB = 7,5{\rm{ cm}}\), \(CD = 12{\rm{ cm}}\).
a) \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}}.\)
b) \(\frac{{BF}}{{FM}} = \frac{{AB}}{{MC}}.\)
c) \(HE = EF = FN\).
d) \(\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}} = \frac{9}{5}\).
Cho hàm số \(y = \frac{3}{2}{x^2} + x - 1.\) Tinh giá trị của biểu thức \(P = \frac{3}{2}f\left( 1 \right) + f\left( 2 \right) - 2f\left( {\frac{1}{2}} \right)\).
(Kết quả ghi dưới dạng số thập phân)
Cho ba đường thẳng \(\left( d \right):y = 3x + 8\), \(\left( {d'} \right):y = 2x + 3\) và \(\left( {d''} \right):y = \left( {2m - 1} \right)x + m - 3\). Xác định giá trị của tham số \(m\) để ba đường thẳng đồng quy.
Tính tổng tất cả các giá trị của \(m\) để phương trình \(\left( {{m^2} - 4} \right)x = m - 2\) vô nghiệm.
Cho tam giác \(ABC\), đường trung tuyến \(AM\). Gọi \(D\) là trung điểm của \(AM,\)\(E\) là giao điểm của \(BD\) và \(AC,F\) là trung điểm của \(EC\). Biết \(AC = 9{\rm{ cm,}}\) hỏi độ dài của đoạn thẳng \(AE\) bằng bao nhiêu centimet?
Cho hàm số \(y = \left( {m - 2} \right)x + 2\) có đồ thị là đường thẳng \(\left( d \right)\).
a) Xác định \(m\) để đường thẳng đi qua điểm \(A\left( { - 1;1} \right).\)
b) Với \(m\) vừa tìm được ở câu a) hãy tìm phương trình đường thẳng \(\left( {d'} \right)\) song song với đường thẳng \(\left( d \right)\) và \(\left( {d'} \right)\) cắt trục tung tại điểm có tung độ bằng \(3\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 8{\rm{ cm,}}\)\(AC = 6{\rm{ cm}}\). Có \(M,N\) là trung điểm của \(AB,AC\).
a) Tính độ dài \(BC,MN\).
b) Vẽ phân giác \(AD\) với \(D \in BC\). Tính độ dài \(BD\).
c) Chứng minh rằng \(BD.AN = AM.DC.\)
Giải phương trình sau: \(\frac{{x - 1}}{9} + \frac{{x - 2}}{8} + \frac{{x - 3}}{7} = \frac{{x - 4}}{6} + \frac{{x - 5}}{5} + \frac{{x - 6}}{4}\).