Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 4)
21 câu hỏi
Điểm nằm trên trục hoành thì sẽ có tung độ bằng bao nhiêu?
\( - 1.\)
\(1.\)
\(0.\)
\(2.\)
Trong mặt phẳng tọa độ \(Oxy\) như hình vẽ.
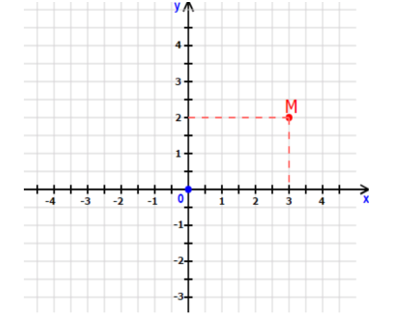
Tọa độ điểm \(M\) là
\(M\left( {3;2} \right).\)
\(M\left( {2;3} \right).\)
\(M\left( {3;0} \right).\)
\(M\left( {0;2} \right).\)
Biến đổi hàm số \(y = 2x + 3y + 1\) về hàm số bậc nhất ta được
\(y = - x - \frac{1}{2}.\)
\(3y = 2x + 1.\)
\(y = - x + 1.\)
\(y = 2x + 1.\)
Công thức biến đổi từ đơn vị độ \(F\) sang đơn vị độ \(C\) là \(C = \frac{5}{9}\left( {F - 32} \right)\). Hỏi nhiệt độ ở \(32^\circ F\) sẽ có giá trị bằng bao nhiêu độ \(C\)?
\(0.\)
\(62.\)
\(32.\)
\(\frac{5}{9}.\)
Phương trình nào dưới đây không phải phương trình bậc nhất một ẩn?
\(\frac{x}{5} + \frac{5}{3} = 0\).
\(1 + 2y = 0\).
\( - 3x + \frac{1}{2} = 0\).
\(2x - {x^2} = 0\).
Đưa phương trình \(2\left( {x + 2} \right) = 1 - 2x\) về dạng \(ax + b = 0\) là
\(4x + 3 = 0\).
\( - 2x + 1 = 0\).
\(4x + 5 = 0\).
\(2x + 4 = 0\).
Một xe tải và một xe con cùng khởi hành từ tỉnh \(A\) đến tỉnh \(B\). Xe tải đi với vận tốc \(30{\rm{ km/h,}}\)xe con đi với vận tốc \({\rm{45 km/h}}\). Nếu gọi quãng đường \(AB\) là \(x{\rm{ }}\left( {{\rm{km}}} \right)\) với \(x > 0\) thì thời gian xe tải đi từ \(A\) đến \(B\) là
\(30x\) giờ.
\(\frac{x}{{30}}\) giờ.
\(40x\) giờ.
\(\frac{x}{{40}}\) giờ.
Một cảnh sát giao thông đang đứng và bắn tốc độ các phương tiện giao thông tham gia trên đoạn đường có biển báo cho phép là \(80{\rm{ }}\left( {{\rm{km/h}}} \right)\). Theo luật giao thông thì vận tốc cho phép các phương tiện giao thông không vượt quá biển báo là \(x{\rm{ }}\left( {{\rm{km/h}}} \right)\). Một ô tô tham gia đi với vận tốc nào sau đây sẽ bị phạt \(\left( {{\rm{km/h}}} \right)\)
\(80 + x.\)
\(80 - x.\)
trên \(80 + x.\)
dưới \(80 - x.\)
Cho tam giác \(ABC\) có \(DE\parallel BC\). Khẳng định nào sau đây là sai?
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC.\)
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC.\)
\(\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}}\) suy ra \(DE\parallel BC.\)
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC.\)
Cho hình vẽ, biết \(ON\parallel MP\).
Khi đó độ dài \(OM\) bằng
\(2{\rm{ cm}}{\rm{.}}\)
\({\rm{4 cm}}{\rm{.}}\)
\({\rm{6 cm}}{\rm{.}}\)
\({\rm{4,5 cm}}{\rm{.}}\)
Cho \(\Delta ABC\) có \(AB = 4{\rm{ cm;}}\)\(AC = 9{\rm{ cm}}{\rm{.}}\) Gọi \(AD\) là tia phân giác của \(\widehat {BAC}\). Tỉ số \(\frac{{CD}}{{BD}}\) bằng
\(\frac{4}{9}.\)
\(\frac{9}{4}.\)
\(\frac{4}{5}.\)
\(\frac{5}{4}.\)
Cho tam giác \(ABC\) có \(I,K\) lần lượt là trung điểm của \(AB,AC\). Biết \(BC = 8{\rm{ cm}}\). Độ dài \(IK\) là
\(4{\rm{ cm}}{\rm{.}}\)
\({\rm{16 cm}}{\rm{.}}\)
\({\rm{2 cm}}{\rm{.}}\)
\({\rm{12 cm}}{\rm{.}}\)
Một xe khách đi từ \(A\) đến \(B\) với vận tốc \(20{\rm{ km/h}}\). Sau \(3\) giờ thì tại A có một xe con đuổi theo với vận tốc \(50{\rm{ km/h}}\). Gọi \(x\) (giờ) là thời gian từ lúc xe con đi tới đuổi kịp xe khách (\(x > 0\)).
a) Thời gian xe khách đi tới lúc gặp xe con là \(x + 3\) (giờ).
b) Quãng đường đi được của xe con là \(50\left( {x + 3} \right)\) (km).
c) Phương trình mô tả bài toán trên là \(20x = 50\left( {x + 3} \right)\).
d) Vậy sau \(3\) giờ thì xe con đuổi kịp xe khách.
Cho tam giác \(ABC\) có đường phân giác \(AD\), biết \(AB = 6{\rm{ cm,}}\)\(BC = 10{\rm{ cm}}\), \(AC = 9{\rm{ cm}}{\rm{.}}\) Trên tia đối của tia \(AB,AC\) lần lượt lấy các điểm \(E,F\) sao cho \(AE = \frac{1}{3}AB,\)\(AC = 3AF\). Qua \(A\) kẻ đường thẳng \(d\) song song với \(BC\) và \(CE\) lần lượt tại \(I\) và \(K\).
a) \(\frac{{AB}}{{BD}} = \frac{{AC}}{{DC}}.\)
b) \(BD = 4{\rm{ cm}}{\rm{.}}\)
c) \(EF\parallel BC.\)
d) \(A\) là trung điểm của \(IK.\)
Cho hàm số \(y = f\left( x \right) = - \frac{{{x^2}}}{2} + 2\). Tình giá trị của biểu thức \(D = 4f\left( {\frac{1}{4}} \right) + f\left( {\frac{1}{2}} \right) - f\left( 1 \right).\)
Cho ba đường thẳng \(\left( d \right):y = x + 2\); \(\left( {d'} \right):y = 3x + 2\) và \(\left( {d''} \right):y = \left( {4 - m} \right)x + 1 + m\). Tìm giá trị của tham số \(m\) để ba đường thẳng đồng quy.
Phương trình \(\frac{2}{3}\left( {x + m} \right) - x + \frac{1}{2} = 0\) nhận \(x = 3\) là nghiệm thì giá trị của \(m\) là bao nhiêu?
(Kết quả ghi dưới dạng số thập phân)
Cho hình dưới đây.
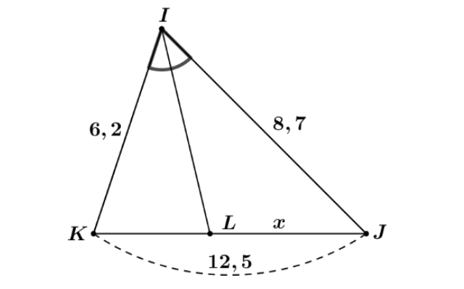
Tính độ dài \(x\). (Kết quả làm tròn đến hàng phần mười)
Cho hai đường thẳng \(\left( d \right):y = 2x + 4\) và \(\left( {d'} \right):y = - \frac{1}{2}x + 1\).
a) Biết rằng \(\left( d \right)\) cắt \(Ox\) tại \(A\), cắt \(Oy\) tại \(B\); \(\left( {d'} \right)\) cắt \(Ox\) tại \(C\), cắt \(Oy\) tại \(D\) và \(Ox\) tại \(A\), cắt \(\left( d \right)\) cắt \(\left( {d'} \right)\) tại \(M\). Biểu diễn đường thẳng \(\left( d \right)\) cắt \(\left( {d'} \right)\) trên hệ trục tọa độ.
b) Tính chu tam giác \(ABC\). (Kết quả làm tròn đến hàng đơn vị)
Cho \(\Delta ABC\) có các đường trung tuyến \(BD,CE\). Gọi \(M,N\) theo thứ tự là trung điểm của \(BE,CD\). Gọi \(I,K\) theo thứ tự là giao điểm của \(MN\) với \(BD\) và \(CE\). Chứng minh rằng:
a) \(DE\parallel BC\).
b) \(MN\parallel BC.\)
c) \(MI = IK = KN.\)
Giải phương trình sau: \(\frac{{x + 1}}{{94}} + \frac{{x + 2}}{{93}} + \frac{{x + 3}}{{92}} = \frac{{x + 4}}{{91}} + \frac{{x + 5}}{{90}} + \frac{{x + 6}}{{89}}\).