Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 3)
21 câu hỏi
Trong các hàm số dưới đây, đâu là hàm số bậc nhất?
\(y = 2x - 3.\)
\(y = \frac{3}{x}.\)
\(y = - 2{x^2} - 3.\)
\(y = \frac{x}{2} + \frac{3}{x}.\)
Tọa độ giao điểm của đồ thị hàm số \(y = \frac{1}{2}x + 3\) với trục tung là
\(\left( { - 3;0} \right).\)
\(\left( {0; - 3} \right).\)
\(\left( {0;3} \right).\)
\(\left( {3;0} \right).\)
Hệ số góc của đường thẳng \(y = \frac{{2x + 1}}{2}\) là
\(1.\)
\(2.\)
\(2x.\)
\(\frac{1}{2}.\)
Hai đường thẳng \(y = ax + b{\rm{ }}\left( {a \ne 0} \right)\) và \(y = a'x + b{\rm{ }}\left( {a' \ne 0} \right)\) song song với nhau khi
\(a = a';b = b'.\)
\(a = a';b \ne b'.\)
\(a \ne a';b \ne b'.\)
\(a \ne a';b = b'.\)
Điều kiện nào dưới đây để phương trình \(ax + b = 0\) là phương trình bậc nhất một ẩn?
\(a = 0\).
\(a \ne 0\).
\(b = 0\).
\(b \ne 0\).
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
\( - x + {x^2} = 0\).
\(\frac{1}{x} + 3 = 0\).
\(\frac{1}{2}x - 3 = 0\).
\(\left( {5x + 3} \right)\left( {2x + 1} \right) = 0\).
Dừa sáp là một trong những đặc sản có giá trị dinh dưỡng cao được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là \(200\) nghìn đồng. Nếu mua \(x{\rm{ }}\left( {x \in \mathbb{N}} \right)\) thì người mua phải trả số tiền (nghìn đồng) là
\(200x.\)
\(\frac{{200}}{x}.\)
\(200 - x.\)
\(\frac{{200{\rm{ }}000}}{x}.\)
Xe máy đi từ \(A\) đến \(B\) với vận tốc \(x\) (km/h). Ô tô đi từ \(B\) về \(A\) với vận tốc nhanh hơn vận tốc của xe máy là \(15{\rm{ km/h}}\). Vậy vận tốc của ô tô được biểu diễn theo \(x\) là
\(x - 15{\rm{ }}\left( {{\rm{km/h}}} \right)\).
\(x + 15{\rm{ }}\left( {{\rm{km/h}}} \right)\).
\(15x{\rm{ }}\left( {{\rm{km/h}}} \right)\).
\(x - 15{\rm{ }}\left( {{\rm{km/h}}} \right)\).
Cho hình vẽ bên, biết \(BC\parallel ED\).
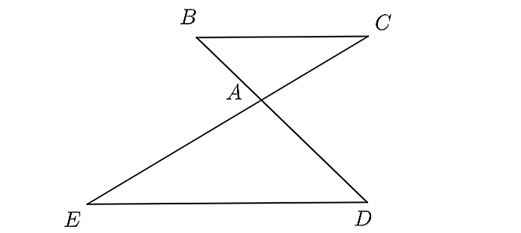
Chọn khẳng định sai trong các khẳng định dưới đây.
\(\frac{{AB}}{{AD}} = \frac{{BC}}{{DE}}.\)
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\)
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{CE}} = \frac{{BC}}{{DE}}.\)
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}.\)
Cho hình vẽ dưới đây.
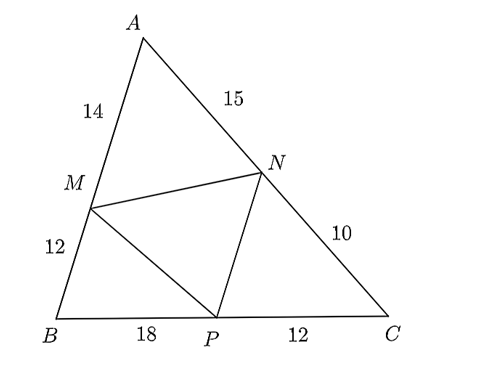
Khẳng định nào sau đây là đúng?
\(MP\parallel AC.\)
\(NP\parallel BM.\)
\(MN\parallel BC.\)
\(MP\parallel AN.\)
Cho \(\Delta ABC\) có \(D,E\) lần lượt là hai điểm nằm trên \(AB\) và \(BC\) sao cho \(\frac{{AD}}{{AB}} = \frac{{CE}}{{CB}}\). Cho các khẳng định sau:
(I). \(DE\) là đường trung bình của \(\Delta ABC\).
(II). \(DE\parallel AC\).
(III). \(\frac{{DB}}{{BA}} = \frac{{DE}}{{AC}} = \frac{1}{2}\).
Khẳng định nào dưới đây là đúng?
Chỉ có (I) đúng.
Chỉ có (II) đúng.
Chỉ có (I) và (III) đúng.
Cả (I), (II) và (III) đều đúng.
Cho hình vẽ dưới đây.
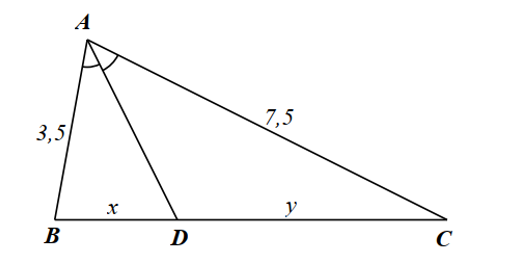
Tỉ số \(\frac{x}{y}\) bằng
\(\frac{7}{{15}}.\)
\(\frac{1}{7}.\)
\(\frac{{15}}{7}.\)
\(\frac{1}{{15}}.\)
Hai lớp \(9A,9B\) có \(80\) học sinh. Trong đợt góp sách ủng hộ vùng khó khăn mỗi em lớp \(9A\) góp \(2\) quyển sách, mỗi em lớp \(9B\) góp \(3\) quyển sách nên cả hai lớp góp được \(198\) quyển. Gọi số học sinh của lớp \(9A\) là \(x\)\(\left( {0 < x < 80,x \in {\mathbb{N}^*}} \right)\).
a) Số học sinh của lớp \(9B\) là \(180 - x\) (học sinh).
b) Số sách lớp \(9A\) và lớp \(9B\) góp được lần lượt là \(2x\) và \(3\left( {80 - x} \right)\) (quyển).
c) Phương trình mô tả bài toán là \(2x + 3\left( {80 - x} \right) = 198\).
d) Số học sinh lớp lớp \(9A\) nhiều hơn số học sinh lớp \(9B\) là \(5\) bạn.
Cho \(\Delta ABC\) có \(DE\parallel BC\) với \(D \in AB,E \in AC\). Kẻ \(EF\parallel CD\) \(\left( {E \in AC,F \in AB} \right)\).
a) \(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}}.\)
b) \(AE.BC = AC.DE\).
c) \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}\).
d) \(\frac{{EF}}{{BC}} = \frac{{DE}}{{CD}}\).
Cho hàm số \(y = f\left( x \right) = 2{x^2} + 3\). Tính giá trị của \(C = 3f\left( 0 \right) - 2f\left( {\frac{1}{2}} \right)\).
Cho ba đường thẳng \(\left( {{d_1}} \right):y = - 2x\), \(\left( {{d_2}} \right):y = 1,5x + 7\), \(\left( {{d_3}} \right):y = mx + 4\). Tìm giá trị của tham số \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) đồng quy.
Cho phương trình \(\left( {4m + 3} \right)x + m = 4{m^2} - 3\). Hỏi có bao nhiêu giá trị \(m\) thỏa mãn để \(x = 0\) là nghiệm của phương trình bậc nhất đã cho?
Cho \(\Delta ABC\). Tia phân giác góc trong của góc \(\widehat A\) cắt \(BC\) tại \(D\). Cho \(AB = 6,AC = x,\)\(BD = 9,BC = 21\). Tìm \(x.\)
Cho hàm số \(\left( d \right):y = 2x\) và \(\left( {d'} \right):y = - x + 3\).
a) Tìm giao điểm \(A\) của hai đường thẳng \(\left( d \right)\) và \(\left( {d'} \right)\).
b) Gọi giao điểm của \(\left( {d'} \right)\) với trục \(Ox\) là \(B\). Tính diện tích tam giác \(AOB\).
Cho \(\Delta ABC\) có đường trung tuyến \(AM\), đường phân giác của \(\widehat {AMB}\) cắt \(AB\) ở \(D\), đường phân giác của \(\widehat {AMC}\) cắt \(AC\) ở \(E\).
a) Chứng minh \(\frac{{AM}}{{BM}} = \frac{{AD}}{{BD}}\).
b) Chứng minh \(DE\parallel BC\) và \(AD.AC = AE.AB\).
c) Gọi \(I\) là trung điểm của \(DE\). Chứng minh ba điểm \(A,I,M\) thẳng hàng.
Giải phương trình sau: \(\frac{{x - 1}}{{2015}} + \frac{{x - 3}}{{2013}} = \frac{{x - 5}}{{2011}} + \frac{{x - 7}}{{2009}}\).