Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 2)
21 câu hỏi
Điểm \(M\left( {{x_0};{y_0}} \right)\) thì \({y_0}\) được gọi là
Hoành độ.
Tung độ.
Gốc tọa độ.
Giao điểm.
Điểm trong mặt phẳng tọa độ có hoành độ âm và tung độ dương sẽ nằm ở góc phần tư thứ mấy?
\(I.\)
\(II.\)
\(III.\)
\(IV.\)
Đồ thị hàm số \(y = ax + b\) với \(a \ne 0\) là gì?
Một đường thẳng.
Một đoạn thẳng.
Một đường cong.
Một đường tròn.
Hệ số \(b\) của đường thẳng \(y = 2\left( {3x - 5} \right) - 7\) là
\( - 7.\)
\( - 5.\)
\(6.\)
\( - 17.\)
Cho các phương trình dưới đây, phương trình bậc nhất một ẩn là
\(\frac{{2x}}{3} + 2 = 0\).
\(\frac{3}{x} + \frac{x}{2} = 0\).
\({x^2} + 2x + 1 = 0\).
\(2x - y = 0\).
Giá trị \(x = - 2\) là nghiệm của phương trình nào trong các phương trình sau?
\(x + 5 = 0\).
\(3x + 1 = 0\).
\(x - 2 = 0\).
\(2x + 4 = 0\).
Nếu một vòi nước chảy đầy bể trong \(5\) giờ thì trong một giờ vòi nước đó chảy được bao nhiêu phần của bể?
\(1.\)
\(\frac{1}{4}.\)
\(\frac{1}{5}.\)
\(\frac{1}{2}.\)
Một ô tô đi từ \(A\) đến \(B\) từ \(6\) giờ sáng, lúc \(7\) giờ sáng cùng ngày, một xe khách cũng đi từ \(A\) và tới \(B\) cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là \(x\) (giờ) thì thời gian đi của ô tô là:
\(x + 1\) (giờ).
\(x - 1\) (giờ).
\(2\) (giờ).
\(x\) (giờ).
Cho \(\Delta ABC\) có \(DE\parallel BC\) như hình dưới đây.
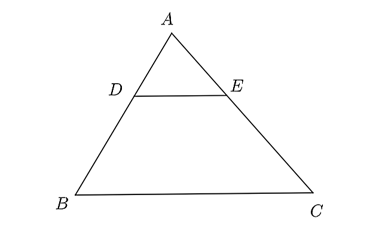
Theo định lí Thalès, ta có:
\(\frac{{AC}}{{CE}} = \frac{{AB}}{{AD}}.\)
\(\frac{{CE}}{{EA}} = \frac{{BD}}{{DA}}.\)
\(\frac{{AC}}{{CE}} = \frac{{BC}}{{CD}}.\)
\(\frac{{AC}}{{BC}} = \frac{{CD}}{{CE}}.\)
Cho hình vẽ dưới đây, biết \(IK\parallel GH\), \(\frac{{FI}}{{FG}} = \frac{1}{3}\).
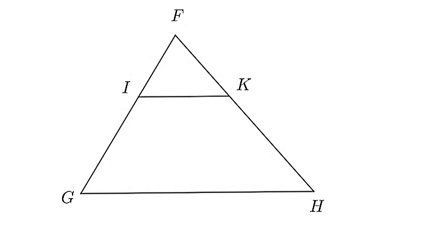
Khi đó, tỉ số nào sau đây có giá trị bằng \(\frac{1}{3}\)?
\(\frac{{FI}}{{IG}}.\)
\(\frac{{FK}}{{FH}}.\)
\(\frac{{FK}}{{KH}}.\)
\(\frac{{GH}}{{IK}}.\)
Cho hình vẽ dưới đây.
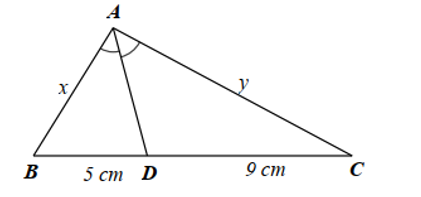
Tỉ số \(\frac{y}{x}\) là
\(\frac{5}{9}.\)
\(\frac{9}{5}.\)
\(\frac{9}{{14}}.\)
\(\frac{{14}}{9}.\)
Cho \(\Delta ABC\) có \(K,F\) lần lượt là trung điểm của \(AB,BC\). Khẳng định nào dưới đây là đúng?
\(KF = 2AC.\)
\(AC = 2KF.\)
\(AC = \frac{1}{2}KF.\)
\(KF = \frac{1}{3}AC.\)
Một ca nô xuôi dòng từ \(A\) đến \(B\) hết \(\frac{4}{3}\) giờ và ngược dòng hết 2 giờ. Biết vận tốc dòng nước là \(3{\rm{ km/h}}\). Gọi vận tốc riêng của ca nô là \(x\) (\(x > 3\), km/h).
a) Vận tốc ca nô xuôi dòng là \(x - 3\) (km/h), vận tốc ca nô ngược dòng là \(x + 3\) (km/h).
b) Quãng đường ca nô xuôi dòng là \(2\left( {x - 3} \right)\) (km) và quãng đường ca nô ngược dòng là \(\frac{4}{3}\left( {x + 3} \right)\) (km).
c) Phương trình mô tả bài toán trên là \(\frac{4}{3}\left( {x + 3} \right) = 2\left( {x - 3} \right)\).
d) Vận tốc riêng của ca nô là \(15{\rm{ km/h}}\).
Cho hình thang \(ABCD\) có \(AB\parallel CD\) và \(AB < CD\). Đường thẳng song song với đáy \(AB\) cắt các cạnh bên \(AD,BC\) theo thứ tự tại \(M,N\).
a) \(\frac{{EA}}{{AD}} = \frac{{EB}}{{BC}}.\)
b) \(\frac{{EA}}{{AM}} = \frac{{BN}}{{BE}}.\)
c) \(\frac{{MA}}{{MD}} = \frac{{NB}}{{NC}}.\)
d) \(\frac{{MD}}{{DA}} = \frac{{BC}}{{NC}}.\)
Cho hàm số \(y = f\left( x \right) = \frac{2}{3}{x^2} - 1\). Tính giá trị của biểu thức \(B = \frac{{3f\left( 1 \right) - f\left( 0 \right)}}{2}\).
Cho ba đường thẳng \({d_1}:y = x - 1\), \({d_2}:y = - x + 1\) và \({d_3}:y = - 3ax + 2a - 1\). Tìm giá trị của \(a\) để hai đường thẳng \({d_1}\) cắt \({d_2}\) tại một điểm thuộc đường thẳng \({d_3}\).
Cho phương trình \(\left( {{m^2} - 9} \right)x = m - 3\). Hỏi giá trị của \(m\) bằng bao nhiêu để phương trình có vô số nghiệm?
Cho tam giác \(ABC\) có \(D,E\) lần lượt là trung điểm của các cạnh \(AB,AC\) và \(DE = 4{\rm{ cm}}\). Biết đường cao \(AH = 6{\rm{ cm}}\). Hỏi diện tích tam giác \(ABC\) là bao nhiêu centimet vuông?
Cho hai hàm số \(\left( {{d_1}} \right)y = - x + 1\) và \(\left( {{d_2}} \right):y = x + 3\).
a) Hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại \(C\) và cắt trục \(Ox\) theo thứ tự tại \(A,B.\) Hãy tìm tọa độ các điểm \(A,B,C\).
b) Xác định đường thẳng \(\left( {{d_3}} \right)\) đi qua điểm \(B\left( {3;0} \right)\) và song song với đường thẳng \(\left( {{d_1}} \right)y = - x + 1\).
Cho tam giác \(ABC\) có \(AB = 4{\rm{ cm,}}\)\(AC = 5{\rm{ cm,}}\)\(BC = 6{\rm{ cm}}\). Các đường phân giác \(BD\) và \(CE\) cắt nhau tại \(I\).
a) Tính \(AD,DC.\)
b) Tính các tỉ số \(\frac{{DI}}{{DB}};\frac{{BE}}{{BA}};\frac{{AD}}{{AC}}\).
c) Tính tỉ số diện tích các tam giác \(DIE\) và \(ABC\).
Giải phương trình sau: \(\frac{{x - 2}}{7} + \frac{{x - 1}}{8} = \frac{{x - 4}}{5} + \frac{{x - 3}}{6}.\)