Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 9)
15 câu hỏi
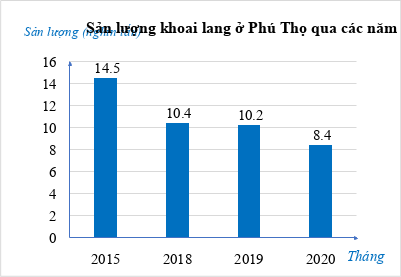
Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
(Nguồn: Niên giám thống kê 2021) |
|
Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
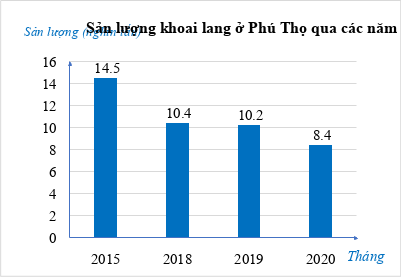
Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
(Nguồn: Niên giám thống kê 2021) |
|
Tổng sản lượng khoai lang ở Phú Thọ cả 4 năm 2015; 2018; 2019; 2020 là bao nhiêu nghìn tấn?
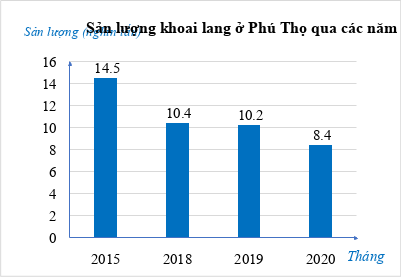
Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
(Nguồn: Niên giám thống kê 2021) |
|
Tính tỉ số phần trăm sản lượng khoai lang ở Phú Thọ trong năm 2020 và tổng sản lượng khoai lang ở Phú Thọ cả 4 năm 2015; 2018; 2019; 2020 (làm tròn kết quả đến hàng phần mười).
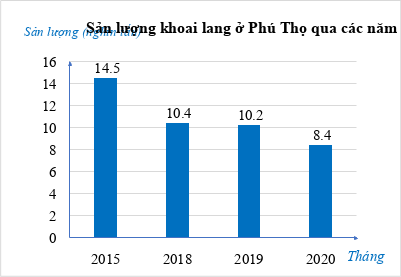
Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
(Nguồn: Niên giám thống kê 2021) |
|
Năm 2019 sản lượng khoai lang ở Phú Thọ tăng hay giảm bao nhiêu phần trăm so với năm 2015 (làm tròn kết quả đến hàng phần mười)? Em có nhận xét gì về sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020.
Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau:
Số khách | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Số ngày | 3 | 6 | 5 | 9 | 3 | 2 | 1 | 1 |
Gọi A là biến cố “Trong một ngày có từ 3 khách trở lên đến cơ quan”. Hỏi có bao nhiêu ngày biến cố A xảy ra?
Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau:
Số khách | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Số ngày | 3 | 6 | 5 | 9 | 3 | 2 | 1 | 1 |
Tính xác suất thực nghiệm của biến cố A.
Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau:
Số khách | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Số ngày | 3 | 6 | 5 | 9 | 3 | 2 | 1 | 1 |
Hãy ước lượng xác suất của biến cố B: “Trong một ngày có số khách đến cơ quan là số lẻ”.
Một hộp có 40 quả bóng được đánh số từ 1 đến 40, đồng thời các quả bóng từ 1 đến 15 được sơn màu vàng và các quả bóng còn lại được sơn màu đỏ; các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Tính xác suất của biến cố sau:
“Quả bóng được lấy ra sơn màu vàng”.
Một hộp có 40 quả bóng được đánh số từ 1 đến 40, đồng thời các quả bóng từ 1 đến 15 được sơn màu vàng và các quả bóng còn lại được sơn màu đỏ; các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Tính xác suất của biến cố sau:“Quả bóng được lấy ra ghi số tròn chục”.
Một hộp có 40 quả bóng được đánh số từ 1 đến 40, đồng thời các quả bóng từ 1 đến 15 được sơn màu vàng và các quả bóng còn lại được sơn màu đỏ; các quả bóng có kích cỡ và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Tính xác suất của biến cố sau:“Quả bóng được lấy ra sơn màu đỏ và ghi số chia hết cho 3”.
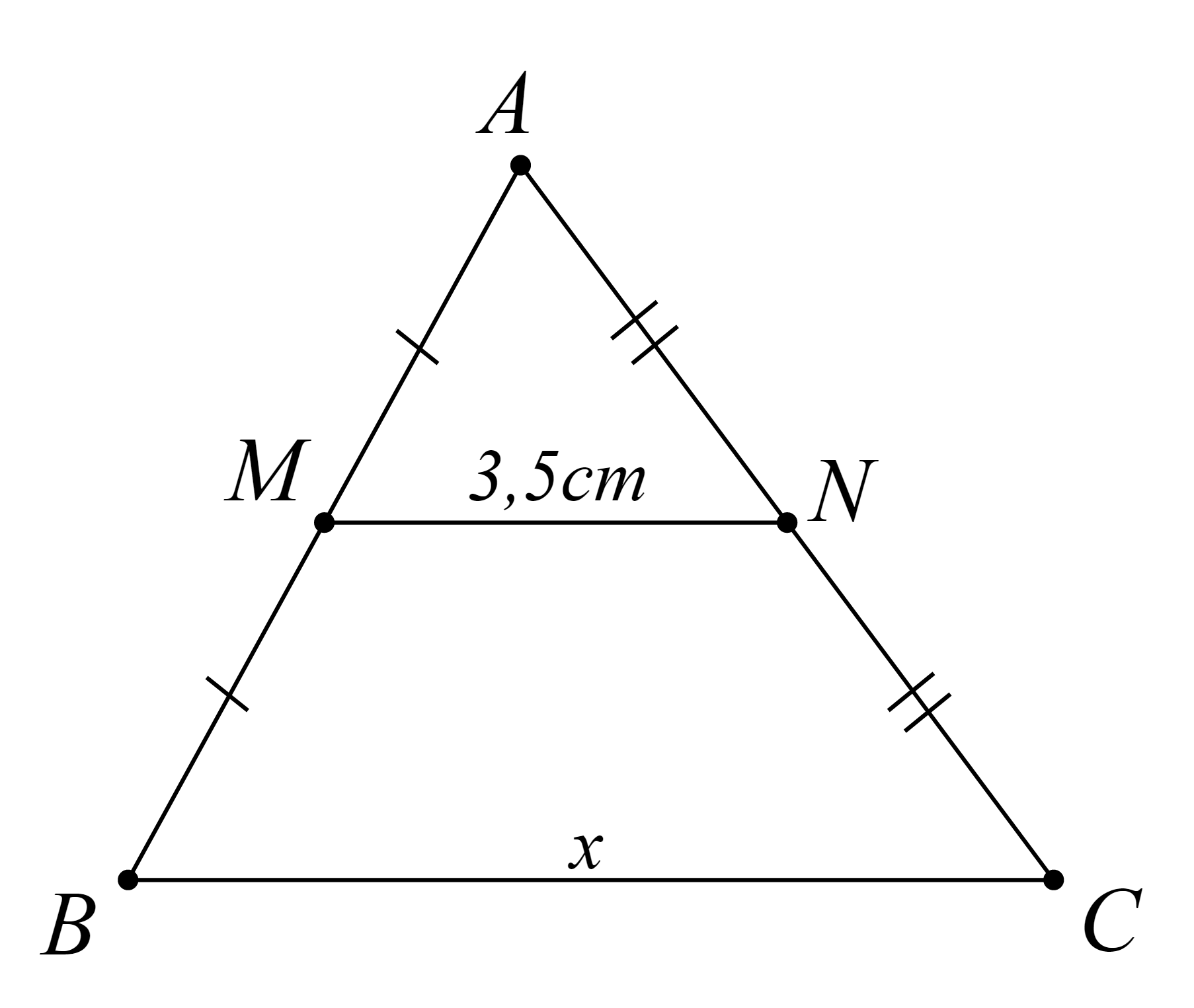
Tìm độ dài ![]() trong mỗi trường hợp sau:
trong mỗi trường hợp sau:
Hình 1 |
Hình 2 |
Cho tam giác ![]() có
có ![]()
![]()
![]() Các đường phân giác
Các đường phân giác ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() Tính
Tính ![]()
Cho tam giác ![]() có
có ![]()
![]()
![]() Các đường phân giác
Các đường phân giác ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() Tính các tỉ số
Tính các tỉ số ![]()
Cho tam giác ![]() có
có ![]()
![]()
![]() Các đường phân giác
Các đường phân giác ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() Tính tỉ số diện tích các tam giác
Tính tỉ số diện tích các tam giác ![]() và
và ![]()
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao ![]() so với mặt đất, chân cọc cách gốc cây
so với mặt đất, chân cọc cách gốc cây ![]() và cách bóng của đỉnh cọc
và cách bóng của đỉnh cọc ![]() Tính chiều cao của cây (kết quả làm tròn đến chữ số thập phân thứ nhất).
Tính chiều cao của cây (kết quả làm tròn đến chữ số thập phân thứ nhất).