Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 5
29 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
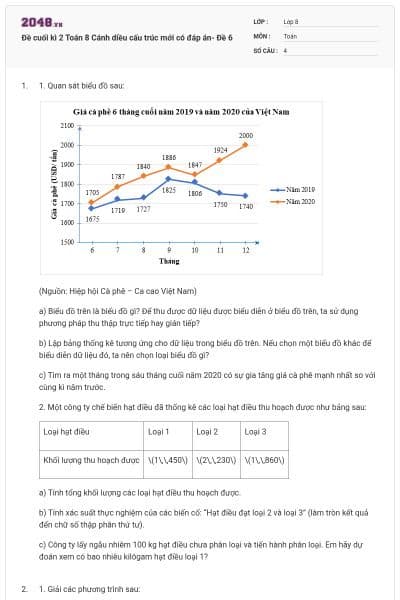
Nhiệt độ trung bình các tháng trong năm của một quốc gia được biểu diễn trong bảng sau:
Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Nhiệt độ (độ C) | 2 | 3 | 5 | 15 | 20 | 30 | 29 | 27 | 20 | 15 | 12 | 7 |
Biểu đồ thích hợp để biểu diễn dữ liệu trong bảng trên là
Biểu đồ hình quạt tròn.
Biểu đồ đoạn thẳng.
Biểu đồ cột tranh.
Không biểu diễn được.
Trong các dãy dữ liệu sau đây, dữ liệu nào là số liệu rời rạc?
Số thành viên trong một gia đình.
Cân nặng (kg) của các học sinh lớp 8D.
Kết quả nhảy xa (mét) của 10 vận động viên.
Lượng mưa trung bình (mm) trong một tháng ở Thành phố Hồ Chí Minh.
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\(0x - 2 = 0.\)
\(2{x^2} + 1 = 0.\)
\(\frac{{x + 3}}{2} = 0.\)
\(\frac{5}{x} + 1 = 0.\)
Phương trình nào sau đây có nghiệm là \(x = 2\)?
\(2x + 1 = 5x.\)
\(2x - 4 = 3x - 9.\)
\(x - 3 = 2x - 5.\)
\(2x - 8 = 3.\)
Gieo một con xúc xắc cân đối đồng chất. Gọi \(A\) là biến cố “Gieo được mặt có số chấm là số lẻ”. Số kết quả thuận lợi là
\(1.\)
\(2.\)
\(3.\)
\(5.\)
Gieo một con xúc xắc cân đối đồng chất. Gọi \(B\) là biến cố: “Gieo được mặt có số chấm là số chẵn”. Xác suất của biến cố \(B\) là
\(\frac{1}{2}.\)
\(\frac{1}{6}.\)
\(\frac{1}{3}.\)
\(\frac{2}{3}.\)
Cho tam giác \(MNP\) có \(H \in MN;K \in MP\). Điều kiện không kết luận được \(HK\parallel NP\) là
\(\frac{{MH}}{{MN}} = \frac{{MK}}{{MP}}.\)
\(\frac{{MH}}{{HN}} = \frac{{MK}}{{KP}}.\)
\(\frac{{HN}}{{MN}} = \frac{{MP}}{{KP}}.\)
\(\frac{{NH}}{{MN}} = \frac{{PK}}{{MP}}.\)
Cho \(\Delta ABC\) có \(BM\) là tia phân giác của \(\widehat {ABC}\)\(\left( {M \in AC} \right)\).
Khẳng định nào sau đây là sai?
\(\frac{{AB}}{{AM}} = \frac{{BC}}{{MC}}.\)
\(\frac{{AB}}{{BC}} = \frac{{AM}}{{CM}}.\)
\(\frac{{BC}}{{AB}} = \frac{{AC}}{{AM}}.\)
\(AM = \frac{{AB.AC}}{{AB + BC}}.\)
Cho hình vẽ bên. Biết \(DE = 13{\rm{ cm}}\), độ dài đoạn thẳng \(HE\) là
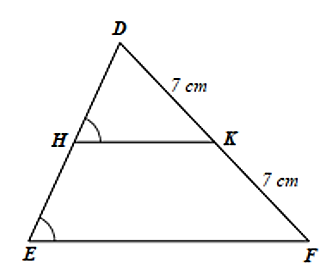
\(5,5{\rm{ cm}}{\rm{.}}\)
\(6,5{\rm{ cm}}{\rm{.}}\)
\({\rm{7 cm}}{\rm{.}}\)
\({\rm{8 cm}}{\rm{.}}\)
Hai tam giác đồng dạng theo trường hợp góc – góc nếu
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
có hai cặp cạnh tương ứng bằng nhau.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh bằng nhau.
Cho hình thang vuông \(ABCD\left( {AB\parallel CD} \right)\) có đường chéo \(BD\) vuông góc với cạnh \(BC\) tại \(B.\)
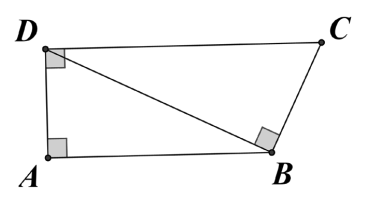
Chọn câu khẳng định đúng.
Cho hình vẽ sau:
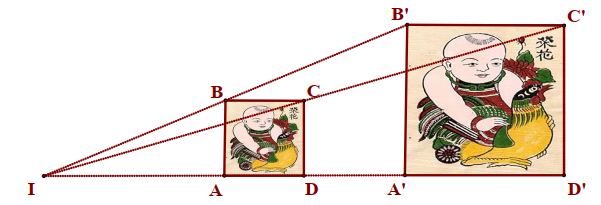
Biết các điểm \(A,B,C,D\) lần lượt là trung điểm các đoạn thẳng \(IA',IB',IC',ID'\). Khẳng định nào sau đây là sai?
Hai tứ giác \(ABCD\) và \(A'B'C'D'\) đồng dạng phối cảnh, điểm \(I\) là tâm đồng dạng phối cảnh.
Hai đoạn thẳng \(AB\) và \(A'B'\) đồng dạng phối cảnh, điểm \(I\) là tâm đồng dạng phối cảnh.
Hai đoạn thẳng \(BB'\) và \[AA'\] đồng dạng phối cảnh, điểm \(I\) là tâm đồng dạng phối cảnh.
Hai đoạn thẳng \(BD\) và \(B'D'\) đồng dạng phối cảnh, điểm \(I\) là tâm đồng dạng phối cảnh.
a) Biểu đồ trên là biểu đồ đoạn thẳng.
b) Để thu được dữ liệu được biểu diễn ở biểu đồ trên, người ta sử dụng phương pháp thu thập trực tiếp.
c) Từ biểu đồ, ta có bảng thống kê như sau:
Năm | 2015 | 2017 | 2018 | 2019 | 2020 |
Vốn (nghìn tỉ đồng) | 6944,9 | 9087,3 | 9465,6 | 9357,8 | 10284,2 |
d) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng khoảng \[148,1\% \] so với năm 2015.
a) \[AD = DE = EC.\]
b) \[I\] là trung điểm của \[AM\].
c) \[{S_{AIB}} = {S_{IMB}}.\]
d) \[{S_{ABC}} = 3{S_{IBC}}.\]
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
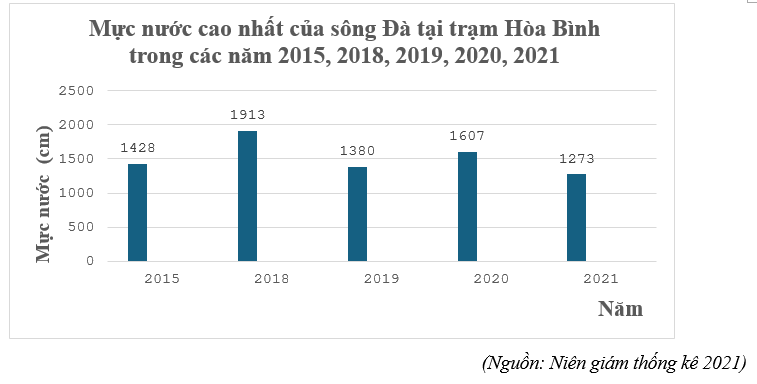
Biều đồ cột ở hình bên dưới thống kê mực nước cao nhất của sông Đà tại tạm Hòa Bình trong các năm 2015, 2018, 2019, 2020, 2021.
Hỏi năm 2021 mực nước cao nhất của sông Đà tại trạm Hoài Bình đã giảm bao nhiêu phần trăm so với năm 2019? (Kết quả làm tròn đến hàng phần trăm)
Có hai túi I và II mỗi túi chứa 5 tấm thẻ được đánh số \(1;2;3;4;5\). Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và nhân hai số ghi trên tấm thẻ với nhau. Tính xác suất của biến cố \(A\): “Kết quả là \(1\) hoặc một số nguyên tố”. (Kết quả ghi dưới dạng số thập phân)
Tìm giá trị của \(x\), biết: \(4\left( {0,5 - 1,5x} \right) = - \frac{{5x - 6}}{3}.\)
Bóng của một cái tháp trên mặt đất có độ dài \(BC = 63{\rm{ m}}{\rm{.}}\) Cùng thời điểm đó, một cây cột \(DE\) cao \(2{\rm{ m}}\) cắm vuông góc với mặt đất có bóng dài \(3{\rm{ m}}\) (hình vẽ).
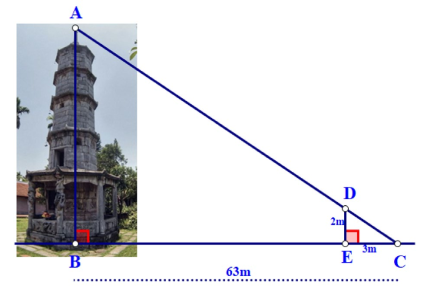
Hỏi tháp cao bao nhiêu mét?
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Có hai loại dung dịch muối I và II. Người ta hòa \(200\) gam dung dịch muối I với \(300\) gam dung dịch muối II thì được một dung dịch có nồng độ muối là \(33\% .\) Tính nồng độ muối trong dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là \(20\% \).
a) Chứng minh rằng
b) Lấy điểm \(I\) thuộc đoạn \(AH\) (\(I\)không trùng với \[A,H\]). Qua \[B\] kẻ đường thẳng vuông góc với \[CI\] tại \[K\]. Chứng minh rằng \[CH.CB = CI.CK.\]
c) Tia \[BK\] cắt tia \[HA\] tại điểm \[D.\] Chứng minh \[CH.CB + DK.DB = C{D^2}.\]
(0,5 điểm) Giải phương trình \(2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9.\)