Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 7
4 câu hỏi
1. Biểu đồ cột kép ở hình bên dưới biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2022 của nước ta.
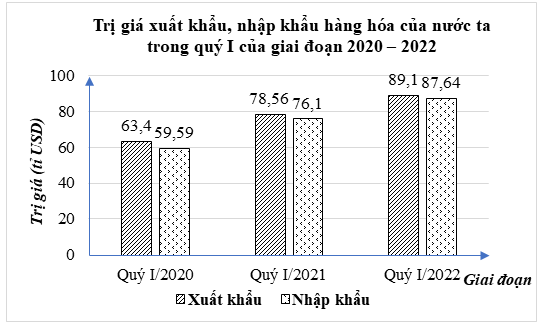
(Nguồn: Tổng cục Hải quan)
a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2022 (đơn vị: tỉ USD) theo mẫu sau:
Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
Xuất khẩu | ? | ? | ? |
Nhập khẩu | ? | ? | ? |
b) Tính tổng trị giá xuất khẩu và hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2 022 là bao nhiêu tỉ USD.
c) Giá trị xuất khẩu hàng hóa của nước ta trong quý I năm 2021 tăng hay giảm bao nhiêu phần trăm so với quý I năm 2020 (làm tròn kết quả đến hàng phần mười)?
2. Một đội thanh niên tình nguyện gồm 11 thành viên đến từ các tỉnh, thành phố như sau: Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk; Đăk Nông; Lâm Đồng; Thành phố Hồ Chí Minh, mỗi tỉnh, thành phố chỉ có đúng một thành viên trong đội. Chọn ngẫu nhiên một thành viên của đội tình nguyện đó.
a) Gọi \(K\) là tập hợp gồm các kết quả có thể xảy ra đối với thành viên được chọn. Tính số phần tử của tập hợp \(K\).
b) Tính xác suất của mỗi biến cố: “Thành viên được chọn ra đến từ vùng Tây Nguyên”.
c) Tính xác suất của mỗi biến cố: “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”.
1. Giải các phương trình sau:
a) \[7x - \left( {12 + 5x} \right) = 6\];
b) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\).
2. Giải bài toán sau bằng cách lập phương trình bậc nhất một ẩn:
Anh Long muốn mua một điện thoại di động iPhone 16 Pro để tặng vợ. Cửa hàng di động có chương trình khuyến mãi lớn, giảm 10% so với giá ban đầu. Do anh Long là khách hàng VIP nên được giảm thêm 5% so với giá đã giảm. Tổng số tiền giảm hai lần là \[3\,\,915\,\,000\] đồng. Hỏi giá ban đầu của điện thoại iPhone 16 Pro là bao nhiêu?
1. Bóng của một cái tháp trên mặt đất có độ dài \[BC = 63{\rm{ m}}.\] Cùng thời điểm đó, một cây cột \[DE\] cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m (hình vẽ). Tính chiều cao của tháp.
![1. Bóng của một cái tháp trên mặt đất có độ dài \[BC = 63{\rm{ m}}.\] Cùng thời điểm đó, một cây cột \[DE\] cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m (hình vẽ). Tính chiều cao của tháp. 2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\] a) Chứng minh: . b) Chứng minh: \(AE \cdot AC = AF \cdot AB\). c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid4-1751277199.png)
2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
b) Chứng minh: \(AE \cdot AC = AF \cdot AB\).
c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\]
Trong túi đựng 48 viên bi có cùng kích thước và khối lượng với hai màu đỏ và xanh. Lấy ngẫu nhiên một viên bi từ túi. Biết rằng xác suất lấy được viên bi màu đỏ bằng 92% xác suất lấy được viên bi màu xanh. Tính số viên bi màu đỏ và số viên bi màu xanh có trong túi.